Совокупность трех чисел может быть представлена как координаты вектора в трехмерном пространстве. Аналогично n=2TF отсчетов, определяющих сигнал, можно представить себе как координаты вектора в воображаемом n-мерном пространстве.

Свойства n-мерного пространства в значительной степени являются обобщением свойств двух- и трехмерного пространства. Длина вектора x=() определяется его нормой ||х||:

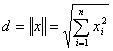(2.117)

Для сигнала s(t) квадрат длины вектора есть умноженная на 2F энергия соответствующего сигнала

(2.118)

непосредственно следует из равенства (2.94). Расстояние между двумя векторами х и у определяется как разности векторов

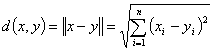(2.119)

Скалярное произведение двух векторов х и у:

(2.120)

Координаты векторов представляют собой проекции вектора х на оси. Если обозначить угол между двумя векторами через а, то получим выражения для

(2.121)

и для проекций х на у и обратно у на х:

Пространство непрерывных функций (сигналов), заданных на интервале 0<t<T, имеет бесконечное число измерений. Для такого пространства скалярное произведение двух векторов определяется соотношением

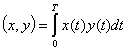(2.122)

а норма и расстояние между векторами:

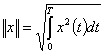(2.123)

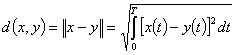(2.124)

Пространство с бесконечным числом измерений представляет собой естественное обобщение n-мерного пространства, получаемое путем предельного перехода от дискретной последовательности к функции непрерывного аргумента. Заметим, что нормы векторов сигналов равны корням из их энергии, а скалярное произведение является мерой корреляции этих сигналов.

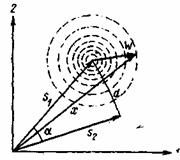
Рис. 2.10. Векторная диаграмма сигнала и помехи

Сигналы конечной длительности Т, ограниченные полосой F, геометрически представляются различными векторами в n-мерном пространстве. Различие между двумя какими-либо сигналами выражается расстоянием между векторами, изображающими их (рис. 2.10). Расстояние зависит от длин векторов и угла между ними, а косинус последнего согласно (2.121) есть не что иное, как коэффициент взаимной корреляции сигналов. Полное отсутствие корреляции (т. е. равенство нулю коэффициента корреляции) выражается ортогональностью векторов ().

Помеха, ограниченная той же полосой, что и сигнал, также определяется вектором из n-мерном пространстве. Этот вектор добавляется к вектору сигнала (рис. 2.10). В отличие от вектора сигнала, вектор помехи может иметь любые величину и направление (вектор является случайным). В результате при наложении помехи на сигнал вокруг конца вектора сигнала образуется «облако», переменная плотность которого выражает вероятность попадания результирующего вектора x=s+w (вектора принятого сигнала) в данный элемент объема. Для флуктуационной помехи это «облако» имеет сферическую форму с эффективным радиусом .

Сообщение (видеосигнал) u(t), не содержащее колебаний с частотами выше Fm, так же как и сигнал, может быть представлено вектором в m-мерном пространстве, где m=2TFm. Совокупность возможных сообщений определяет это пространство (пространство сообщений). На рис. 2.11 представлена двухмерная модель этого пространства с двумя различными сообщениями и и2.

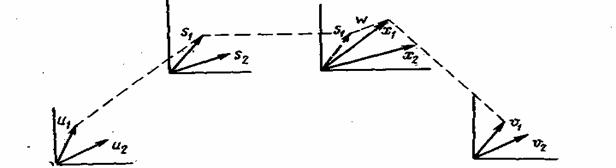
Рис. 2.11 Геометрическая модель системы связи

При передаче сообщение u(t) преобразовывается в сигнал s(t) с использованием некоторого переносчика f(t). Математически эту операцию формирования сигнала можно представить в виде

(2.125)

где М — оператор, в общем случае нелинейный. Геометрически формирование сигнала может быть представлено как преобразование пространства сообщений U в пространство сигналов S: векторы и и2.

преобразуются в векторы s1 и s2.

Мерность пространства сообщений т в общем случае не равна мерности пространства сигналов m. При однополосной передаче m=п. В случае амплитудной модуляции сигналы имеют вдвое большее число координат, чем сообщения: n=2m, а при частотной пространство сигналов имеет значительно большее число измерений, чем пространство сообщений.

При наложении помехи на сигнал создается область неопределенности, в которую попадают принятые сигналы x=s+ω. Взаимодействие сигнала и помехи можно выразить оператором

(2.126)

Оператор Ψ преобразует пространство сигналов S в пространство принятых сигналов X: векторы s1 и s2 переходят в x1 и х2.

Приемник по принятым сигналам х воспроизводит переданное сообщение

(2.127)

т. е. преобразует пространство сигналов X в пространство принятых сообщений V.

Если помеха отсутствует, то принятый сигнал преобразуется в сообщение обратным оператором . В этом случае принятое сообщение тождественно переданному .

При наличии помех сообщения на приеме воспроизводятся с некоторой ошибкой: вместо сообщения может быть воспроизведено сообщение и2наоборот. Ошибка произойдет, когда результирующий вектор х окажется ближе к концу вектора того сигнала s, который в данный момент не передается. Можно построить приемник, воспроизводящий сообщение всякий раз, когда конец вектора х ближе к концу вектора , чем к концу вектора s2 и наоборот. Такой приемник по Котельникову называется идеальным или оптимальным. Очевидно, ошибка при оптимальном приеме будет тем меньше, чем больше расстояние d между соседними сигналами. Это расстояние, в свою очередь, зависит от расстояния r между соседними сообщениями и от вида оператора М, который определяет способ формирования сигнала (в частности, способ модуляции).