Случайный процесс, энергетический спектр которого сосредоточен в относительно узкой полосе частот вблизи некоторой частоты , называется узкополосным процессом. Узкополосный СП имеет место, например, на выходе резонансного усилителя при подаче на его вход широкополосного случайного процесса вида «белого шума». Так как спектр такого СП сосредоточен вокруг частоты его можно представить в виде квазигармонического (почти гармонического) колебания

, (5.84)

где и – соответственно огибающая и начальная фаза, которые являются случайными медленно меняющимися (по сравнению с ) функциями.

Воспользовавшись известным тригонометрическим соотношением

,

представим (5.84) в виде

или

, (5.85)

где ;

. (5.86)

В свою очередь ;

. (5.87)

Для определения статистических характеристик огибающей и фазы удобно представить узкополосный случайный процесс в комплексной форме

. (5.88)

Вещественная часть

(5.89)

и мнимая часть

(5.90)

являются комплексно-сопряженными процессами, связанными между собой преобразованиями Гильберта

; .

Напомним, что сигнал , сопряженный с получается при повороте фаз всех гармонических составляющих на угол .

Теперь с учетом (5.89) и (5.90) выражение (5.88) можно представить следующим образом

. (5.91)

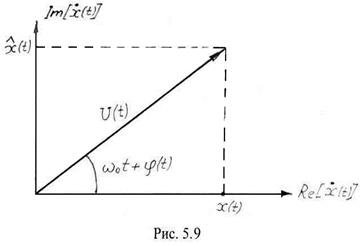
Графически комплексный случайный процесс изображается на комплексной плоскости вектором случайной длины и случайным фазовым углом , который вращается с частотой ротив часовой стрелки (рис. 5.9). в момент времени этот вектор образует с вещественной осью полный угол .

Приведем некоторые соотношения, характеризующие и . В первую очередь отметим, что энергетические спектры и одинаковы, т.е.

. (5.92)

Если энергетические спектры одинаковы, то в соответствии с теоремой

Винера–Хинчина одинаковыми будут и автокорреляционные функции

. (5.93)

Функция взаимной корреляции при

, (5.94)

т.е. в совпадающие моменты времени значения и не коррелированны.