4.4.1. Оценка внешних механических нагрузок, действующих на ОК

4.4.2. Расчет механической прочности оптического кабеля и выбор конструкции

4.4.1. Оценка внешних механических нагрузок, действующих на ОК

Для правильной оценки внешних механических нагрузок, действующих на оптический кабель, следует рассмотреть сначала механизм разрушения оптических волокон под воздействием механических напряжений.

Растягивающие нагрузки. Такие нагрузки ОК делятся на постоянные и переменные, статические и динамические. Прочность оптического волокна определяется в основном наличием поверхностных трещин, которые произвольно располагаются вдоль всей его длины. Величина прочности зависит от длины образца оптического волокна, скорости приложения нагрузки и условий окружающей среды. Если к волокну не прикладывать нагрузок, то его механические и оптические свойства остаются неизменными, даже если на волокно воздействуют влага, вода, кислоты большой концентрации или другие химические вещества. Если к волокну прикладывать напряжение, то трещины на его поверхности могут увеличиваться. Таким образом, волокна, которые подвергаются растягивающему напряжению, кручению или перегибам, подвергаются воздействию статической усталости, что со временем приводит к ухудшению их прочностных характеристик.

Обычно при изготовлении оптические волокна подвергаются тестированию на механическую прочность, т.е. испытаниям на перемотку под натяжением по всей их длине. В результате использование волокон с низкой механической прочностью для изготовления оптических кабелей исключается.

Для выбора конструкции оптического кабеля необходимо помнить, что в процессе прокладки и эксплуатации кабель подвергается комплексному воздействию различных механических нагрузок. Рассмотрим важнейшие из них.

Постоянные статические нагрузки действуют, например, на кабель, намотанный под натяжением на барабан. Этот вид нагрузок вызывает усталостные напряжения, которые особенно в присутствии влаги могут вызвать разрушение оптического волокна при нагрузках, значительно меньших обеспечиваемых прочность материала, из которого оно изготовлено. Существующие модели, описывающие поведение кварцевого оптического волокна при воздействии статических усталостных напряжений, не дают возможность осуществить долгосрочное(свыше одного года) прогнозирование его поведения [3]. На рис.4.5 представлена зависимость момента наступления разрыва от относительной влажности и начальной деформации, полученная в рамках одной из разработанных моделей [8].

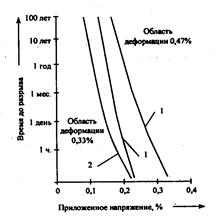
Рис. 4.5. Зависимость времени наступления разрыва от приложенной нагрузки: 1 – относительная влажность 2%; 2 – относительная влажность 97%

Статические усталостные напряжения можно предотвратить, регулируя отношение напряжения растяжения волокна к максимальному кратковременному разрушающему напряжению. Применение специальных мер по защите волокна от влаги, таких как желеобразные, заполнения или металлические оболочки, также значительно увеличивает стойкость кабеля к данному виду нагрузок.

Переменные статическая и динамическая нагрузки воздействуют на оптический кабель при его прокладке или опускании в скважину. При этом величина такой нагрузки определяется тяговым усилием лебедки (спускаемого груза), прикладываемым к концу кабеля, и собственного веса кабеля с учетом коэффициента трения кабеля о поверхность трубы (скважины). Динамические нагрузки возникают при заклинивании кабеля в трубе или скважине, резком ускорении или торможении тяговой лебедки и пр. Упрощенный инженерный расчет внешней растягивающей силы, действующей на кабель при переменной статической нагрузке, может быть проведен по следчошим формулам [9]:

• для воздушной прокладки (без учета ветровых нагрузок, обледенения и температуры) 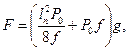(4.34)

• при прокладке кабеля в грунте (сила натяжения кабеля на выходе из кассеты кабеле прокладочного ножа) 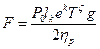, (4.35)

где F — растягивающая нагрузка ОК, Н; P₀ — погонный вес кабеля, кг/км; l_n— расстояние между точками подвеса, м; f— стрела провеса, м; l_к — расстояние между осью кабельного барабана и осью направляющего ролика кабелеукладчика, м; ζ — угол изгиба кабеля в кассете, рад; η_р— коэффициент полезного действия направляющего ролика; Т — коэффициент трения между материалами оболочки ОК и кассеты кабелепрокладочного ножа; g—ускорение свободного падения.

Формулы для расчета растягивающей силы, действующей на ОК при прокладке в кабельной канализации, приведены в разд. 7.1.2.

При эксплуатации кабеля в скважинах или при подводной прокладке растягивающие усилия определяются по выражению:

, (4.36)

где Н_макс — максимальная глубина прокладки кабеля, м; Р_0к— вес единицы длины кабеля с учетом закона Архимеда для среды, в которой осуществляется прокладка кабеля, кг; Р_об —вес спускаемого объекта с учетом закона Архимеда для среды, в которой осуществляется прокладка, кг; k_з — коэффициент запаса (k_з = 2,5 — 3,0).

Вес любого изделия с учетом закона Архимеда

, (4.37)

где Р_в — вес изделия в воздухе, кг; V_в — объем вытесняемой изделием жидкости, м³; γ_в— удельный вес жидкости (для морской воды γ_в = 1,1·10³ кг/м³ ).

При подъеме кабеля с мелководья необходимо учитывать, что кабель извлекается из грунта. При этом справедливо следующее выражение для k_з:

(4.38)

где ,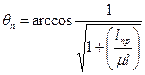

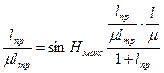
(θ_п— угол подъема кабеля, град.; l — общая длина кабеля от точки подъема до точки приема на барабан, м; μ — постоянная трения на дне; l_тр — длина кабеля, на которую воздействует трение на дне, м; l_пр — провис кабеля, м).

Если провис кабеля составляет 3% и постоянная сила трения 0,3, а угол подъема кабеля равен 45^о, то усилие подъема кабеля в 3,2 раза больше его веса. При подъеме с глубины 1,5 км длина поднимаемого кабеля составляет 4,8 км.

При подъеме кабеля с больших глубин длина поднимаемого отрезка обычно не велика (подъем кабеля осуществляется по частям).

Соотношение между натяжением кабеля и его относительным удлинением для конструкций морских ОК можно получить исходя из следующего выражения:

, (4.40)

где ε_к— относительное удлинение кабеля; Е_а — модуль Юнга армирующей проволоки; S_а— площадь поперечного сечения армирующей проволоки, мм; Е_МТ — модуль Юнга металличккой трубки, ГПа; S_MT — площадь поперечного сечения металлической трубки, мм.

Изгибающие нагрузки. Этот вид нагрузок возникает при прохождении кабеля через ииправляющие ролики при его размотке и прокладке или через ролик блок-баланса. Величина этих нагрузок зависит от величины натяжения кабеля F и радиуса ролика и может быть найдена из выражения:

, (4.40)

где F_изг — изгибающая нагрузка, Н; k_ж — коэффициент жесткости, определяемый опытным путем и зависящий от конструкции кабеля и радиуса ролика.

Раздавливающие нагрузки. Величина раздавливающей нагрузки (давления) q, приходящаяся на единицу длины кабеля, определяется по формуле:

, (4.41)

где q — раздавливающая нагрузка, Н/мм²; R — радиус ролика, мм.

Истирающие нагрузки непосредственного влияния на оптическое волокно не оказывают, если сохранена целостность защитной оболочки, и в дальнейшем рассматриваться не будут.

Гидростатическое давление. Расчет гидростатического давления на ОК F_r. Для царских кабелей, в конструкцию которых мажет входить тонкостенная металлическая трубка, можно рассчитать по формуле:

(4.42)

Гидростатическое давление для толстостенной трубки можно определить по формуле:

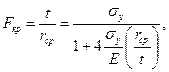(4.43)

где Е — модуль Юнга, ГПа; μ — коэффициент Пуассона; t — толщина трубки, мм; r — радиус трубы, мм; F_кр — критическое гидростатическое давление; r_ср — средний радиус трубки, мм; σ_у — предел текучести материала трубки, см³/кгс.

4.4.2. Расчет механической прочности оптического кабеля и выбор конструкции

Целью расчета механической прочности по заданным нагрузкам является определение возникающих в ОК деформаций, из-за которых могут возникнуть нежелательные изменения характеристик ОВ.

Величина деформации кабеля (относительное удлинение), и следовательно ОВ, не должна превышать некоторой заданной величины, обеспечивающей его надежную работу в течение всего срока службы.

Зная величины F и F_изг и задаваясь удлинением ОВ, можно рассчитать элементы конструкции ОК.

Расчет конструкций ОК по заданным растягивающим нагрузкам. Величина растягивающей нагрузки, обеспечиваемая конструкцией ОК, определяется выражением вида:

(4.44)

где Е_i — модуль Юнга элементов ОК (демпфера, оболочек, брони и пр.); S_i — площадь поперечного сечения элементов ОК; ε_OK — относительное удлинение ОК; п_OB — число ОВ в ОК; θ=arctg(2πA/h) — угол скрутки волокна к оси ОК; А — радиус скрутки; S_OB — площадь поперечного сечения ОВ; ε_OB — относительное удлинение ОВ; h — шаг скрутки ОВ.

Величины ε_OK и ε_OB в общем случае не равны друг другу, т.к. ОВ в кабеле может иметь некоторую избыточную длину, величина которой позволяет избежать деформации ОВ в начальные периоды деформации ОК. Другими словами, необходимо создать такую конструкцию ОК, чтобы ОВ не подвергалось деформации, пока кок не достигнет некоторого критического значения.

При конструировании ОК допустимую величину ε_OB можно принимать равной 0,25 % [2].

Конструкция ОК со скрученными вокруг центрального элемента ОВ в ПЗО. Рассмотрим упрощенную модель концентрического оптического кабеля (рис. 4.6) [11]. Сердечник содержит армирующий элемент, в демпфере находится определенное количество и оптических волокон в полимерном покрытии, скрученных вокруг сердечника с некоторым шагом h.

При воздействии на оптический кабель растягивающей силы при сохранении целостности волокон должно выполняться условие равновесия сил вдоль оси оптического кабеля [3]:

, (4.45)

где E_с, Е_Д, Е_об, S_с,S_Д, S_об — модули упругости и площади сечений сердечника, демпфера и оболочки соответственно,

(4.46)

где ε_ОВ — относительное удлинение оптического волокна в полимерной оболочке; E_о, E_П, S_о, S_П – модули упругости и площади сечений оптического волокна и защитной полимерной оболочки; F_ОВ — сила натяжения каждого оптического волокна, направленная под углом скрутки θ к оси.

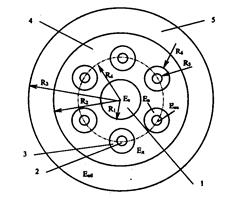
Рис. 4.6. Упрощенная модель для расчета деформаций в концентрическом оптическом кабеле: 1 – сердечник с армирующим элементом; 2 – опьическое волокно; 3 – защитная полимерная оболочка волокна; 4 – демпфер; 5­ – защитная оболочка

Радиус кривизны винтовой линии, по которой уложено оптическое волокно, определяется как , а нормаль к винтовой линии пересекает ось оптического кабеля. Для расчета механической прочности такого ОК следует использовать расчетную схему, приведенную на рис.4.6.

Для ОВ в ПЗО при его натяжении появляется нормальная поперечная сила, которая сжимает внутренние слои ОК, уменьшая А. Расчет деформаций ОВ при воздействии растягивающей нагрузки может быть выполнен следующим образом.

Нормальная поперечная сила, сжимающая внутренние слои демпфера сердечника и полимерной оболочки волокна, выражается в виде:

(4.47)

При этом радиус скрутки ОВ уменьшается на δ_А=ε_АА, где ε_А составляет относительное удлинение материалов по радиусу А. Тогда относительное удлинение оптического волокна в полимерной оболочке можно определить с помощью выражения [3]:

. (4.48)

Сжатие δ_А является суммой деформаций трех слоев. Приближенно оно выражается в виде:

, (4.49)

где — модуль Юнга центрального элемента в поперечном направлении; R_i — радиусы элементов ОК, представленные на рис. 4.6.

На рис. 4.7 показана рассчитанная по формулам (4.45) — (4.49) зависимость допустимой силы растяжения оптического кабеля F_Д и относительного удлинения кабеля ε_ОК при заданном допустимом удлинении оптического волокна ε_ОВ=0,25 %. Расчет проведен при следующих параметрах:

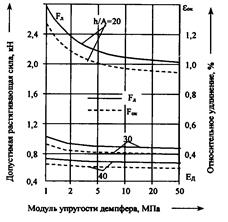
Рис. 4.7. Зависимость допустимой силы растяжения оптического кабеля FД и относительного удлинения кабеля εОК от модуля упругости демпфера при εОВ=0,25%

Таким образом, алгоритм расчета деформации ОВ в конструкции ОК с повивной скруткой волокон в ПЗО при воздействии растягивающих нагрузок может быть представлен в следующем виде:

1) определяется внешняя растягивающая сила, действующая на ОК по одному из выражений (4.34), (4.35), (4.36) в зависимости от области его применения при этом ее значение не должно превышать значение принятого допустимого растягивающего усилия F_Д, обеспечиваемого конструкцией ОК, т.е. F≤ F_Д.

2) для выполнения расчетов конструкции ОК, обеспечивающей F_Д, задаются значения , Е_i, R_i, S_i, п_ОВ, h, ρ, r, соsθ, A, Е_OB, S_OB, E_П, S_П, исходя из принятых моделей конструкции кабеля и волокна; при этом ε_ОВ=0,25 %;

3) определяется удлинение ОК — едк с помощью выражения (4.47) по заданному значению F_Д;

4) с помощью (4.46), (4.47) и (4.49) вычисляются F_ОВ, F_П, δ_А соответственно;

5) на основании известных уже А и о„рассчитывается значение относительного удлинения материалов по радиусу:

(4.50)

6) используя (4.48), определяется расчетное значение удлинения волокна (ε_{ОВ расч}) и сравнивается с заданным. В случае выполнения неравенства (ε_{ОВ расч} ) > ( ε_{ОВ зад}) проводят корректировку конструкции ОК с последующим расчетом по этому алгоритму, добиваясь неравенства (ε_ОВрасч ) ≤ ( ε_{ОВ зад}).

Конструкция ОК со скрученными вокруг центрального элемента ОВ в трубчатой защитной оболочке. Упрощенная модель сердечника такого ОК приведена на рис. 4.8.

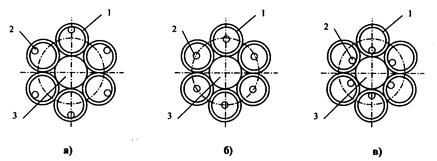
Рис. 4.8. Упрощенная модель для расчета деформации ОВ в ТЗО при охлаждении (а), нормальных условиях (б) и нагревании (в) в скрутке:

1 – ТЗО; 2 – ОВ; 3 – сердечник с армирующим элементом

Расчет конструкции ОК по механической прочности выполняется аналогично предыдущей конструкции.

При этом радиус кривизны винтовой линии, по которой уложено ОВ, определяется по

выражению:

(4.51)

где А_Г — радиус геликоиды, образованной ТЗО (трубкой оптического модуля) в скрутке, мм.

В свою очередь А_Г вычисляется по выражению:

, (4.52)

где R_ТЗО — радиус трубчатой защитной оболочки.

Для ОВ в T3О его избыточная длина, а следовательно, и удлинение, определяются по выражению:

(4.53)

где r — расстояние между центрами T3О и ОВ в данной оболочке; Р — шаг скрутки ОВ в ТЗО.

Выражение (4.53), взятое со знаком плюс, соответствует случаю, представленному на рис.4.8 а, со знаком минус — на рис. 4.8 в. В нормальных условиях ε_ОВ =0 (рис. 4.8 б).

Используя выражение (4.53), аналогично расчетам предыдущей конструкции ОК находится расчетное значение ε_{ОВ расч} и сравнивается с заданным значением ε_{ОВ зад}.

При нормальных условиях (рис. 4.8 6) и при охлаждении ОК (рис. 4.8 а) удлинение ε_ОВ>>ε_А.

При этом ε_{ОВ расч} рассчитывается по выражению (4.53) или выражению вида:

, (4.54)

где α_ТЗО, α_ОВ — температурные коэффициенты линейного расширения T3О и ОВ соответственно 1/^оС; Т — рабочая температура, ^оС; Т, — нормальная температура, ^оС.

Конструкция ОК с профилированным сердечником. Для конструкции ОК с профилированным сердечником при воздействии растягивающего усилия ОВ перемещается внутри паза. Размер паза определяет допустимую продольную относительную деформацию ОК. Расчет относительного удлинения сердечника ОК с учетом (4.45) осуществлен для модели, представленной на рис. 4.9 в предположении, что ОВ не подвержено воздействию растягивающей силы. При приложении к ОК (сердечнику) растягивающей силы происходит смещение ОВ в пазу до соприкосновения его с дном канавки.

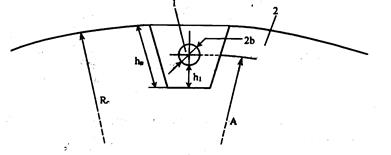
Рис. 4.9. Модель для расчета деформации ОВ в профилированном сердечнике: 1-ОВ; 2-сердечник

В этом случае длина ОВ в пазу сердечника определяется по выражению вида:

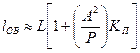, (4.55)

где l_ОВ — длина ОВ, м; L — длина ОК, м; P — шаг скрутки ОВ в пазу, мм; К_П = 2π²; А — радиус скрутки ОВ, мм.

В этой модели радиус кривизны ОВ для спиральной укладки определяется из следующего выражения:

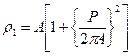. (4.56)

Относительное удлинение ОК определяется выражением (4.58).

Для реверсивной скрутки профилированный сердечник может быть выполнен в виде, представленном на рис. 4.10. В этом случае расчет проводят в соответствии с (4.55) и выражениями по определению радиуса кривизны ОВ для реверсивной укладки (ρ₂) и относительного удлинения ОК (ε_ОК), которые представляются в виде:

. (4.57)

где z — продольная координата;

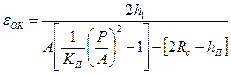, (4.58)

где - для реверсивной укладки ОВ и К_П=2π² — для спиральной укладки ОВ; h₁ -расстояние от нижней точки поверхности волокна до дна паза; R_с — радиус по внешней поверхности оболочки; h_Р — глубина паза.

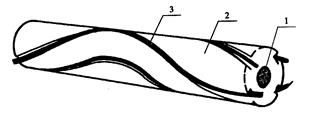
Рис. 4.10. Общий вид профилированного сердечника

с ОВ, уложенным методом разнонаправленной скрутки:

1 — армирующий элемент; 2- профилированный сердечник;

3- паэ профилированного сердечника с ОВ

Увеличение ε_ОК из-за уменьшения р ограничено напряжениями, возникающими в ОВ при малых радиусах изгиба.

Как указано в [2, 3] разнонаправленная скрутка обеспечивает более точную регулировку натяжения ОВ.

Анализ полученных выражений (4.55), (4.58) показывает, что максимальное относительное удлинение ОК при минимальных напряжениях в ОВ получается при минимальном шаге скрутки. При спиральной укладке радиус кривизны ОВ остается постоянным по всей длине, в то время как при реверсивной скрутке он меняется.

Расчет конструкции ОК по заданным изгибающим нагрузкам. При конструировании ОК представляет интерес определение его механической прочности при растяжении, исходя из вероятности разрушения ОВ при растяжении. Предположим, что в ОК есть пол, имеющих одинаковые: длину, S_OB σ_{0 p} и m— постоянные, определяемые из распределения Вейбула. Тогда

, (4.59)

где σ_0p — разрушающее напряжение при вероятности разрыва 63,2% [2, 3].

Изгиб концентрического ОК радиуса R рассматривается для случая, когда длина осевой линии ОК остается неизменной. Тогда длина деформированной винтовой линии (рис. 4.10) в первом приближении также не меняется. Радиус кривизны р винтовой линии при изгибе меняется от точки к точке. Уравнение винтовой линии можно записать в двух системах координат:

1) в цилиндрической

, (4.60)

где r — радиус, φ — полярный угол, h — шаг винтовой линии.

2) в декартовой

Шагу h винтовой линии соответствует .

Участки оптического волокна с внешней стороны изогнутого оптического кабеля растягиваются, а с внутренней — сжимаются.

Вдоль волокна возникают продольные уравновешивающие силы.

Рассмотрим два возможных случая расположения оптического волокна в кабеле: свободное размещение волокна относительно других элементов конструкции кабеля (демпфера) и плотное соединение волокна с демпфером.

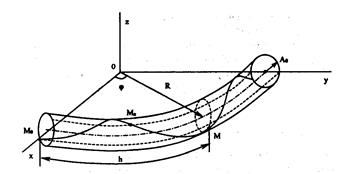
Рис. 4.11. Схематический чертеж расположения оптического волокна в кабеле при его изгибе

При свободной укладке оптического волокна в кабеле, например, в трубке из полимерного материала или в пазах сердечника, в нем возникают только деформации изгиба, зависящие от его наружного радиуса Ь и радиуса кривизны р. Наружная часть изогнутого оптического волокна растягивается, а внутренняя сжимается с ε_изг. Напряжения в крайних точках сечения оптического волокна равны между собой по величине и противоположны по знаку: σ_± = ± ε_изг E₀. Деформация уменьшается с увеличением шага h (рис. 4.11). Она также меньше, если радиус скрутки А мал, однако при малых радиусах изгиба R положение меняется, к меньшим деформациям приводит выбор большего А. Расчет значений ε_изг на рис. 4.12 проведен для тех же условий, что и расчет F_Д, приведенный выше, при этом Е_Д= 1 МПа.

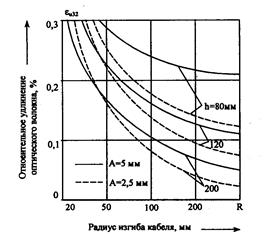
Рис. 4.12. Зависимость относительного удлинения оптического волокна при изгибе от радиуса кабеля и шага скрутки (2b=150 мкм)

Продольная уравновешивающая сила может появляться и при свободной укладке оптического волокна в кабеле вследствие его касания элементов кабеля и проскальзывания при изгибе кабеля. Она зависит от коэффициента и характера трения и скорости изгибания. Последняя определяется скоростью намотки оптического кабеля на барабан или скоростью прохождения кабеля через изогнутый участок при протяжке.

С наибольшей скоростью перемещаются точки с , т. е. находящиеся посередине между М₀ и М_р.

Скорость проскальзывания и соответствующие напряжения увеличиваются с ростом шага скрутки. Для уменьшения напряжений при перемещениях оптического волокна следует ограничить величину шага скрутки, коэффициент трения оптического волокна и скорость изгибания оптического волокна.

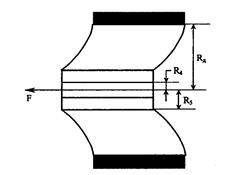
Рис. 4.13. Схема модели для расчета относительного удлинения оптического волокна при изгибе и плотной укладке в конструкции кабеля

Если оптическое волокно скреплено с демпфером, то его сохранность при изгибе, т. е. его малые деформации, могут быть обеспечены за счет мягкости материала демпфера, который допускает как продольное, так и поперечное перемещение оптического волокна относительно остальных элементов конструкции оптического кабеля. При этом в демпфере, волокне и его покрытии возникают определенные напряжения, стремящиеся вернутьвсе точки конструкции в исходное положение. Для расчета возникающих напряжений рассмотрим следующую модель (рис.4.13).

Каждое оптическое волокно в полимерном покрытии окружено воображаемым коаксиальным с ним цилиндром радиусом R=(R₂–R₁)/2, который касается элементов сердечника и защитной оболочки и прочно с ними связан. При изгибе оптического кабеля все точки на окружности этого цилиндра, как и точки конструктивных элементов оптического кабеля в любом его поперечном сечении, остаются в одной плоскости, в то время как сердечник и светоотражающая оболочка волокна смещаются вдоль своей оси.

Расчет относительного удлинения ОВ при изгибе может быть выполнен следующим образом.

В [1, 2] показано, что решение задачи определения относительного удлинения сердечника и светоотражающего покрытия оптического волокна для данного случая довольно сложное, и конечное решение для расчета ε_ОВ имеет следующий вид:

(4.61)

где D=E_ОВS_ОВ/k_y; ω_L=2π/l — пространственная круговая частота винтовой линии с радиусом ρ; k_y — коэффициент упругости материала демпфера.

Демпфер действует как пружина и создает возвращающую силу. Связывая величину коэффициента упругости со свойствами материала демпфера с помощью соотношения:

(4.62)

где G_Д — коэффициент Пуассона, μ_Д — модуль сдвига) и определяя полный сдвиг с помощью закона Гука, можно выразить коэффициент упругости материала демпфера, как

. (4.63)

Результаты расчета по приведенным формулам относительных удлинений при изгибе показаны на рис. 4.14. Расчет проведен для следующих параметров:

Расчеты показывают, что при модуле упругости демпфера Ед, равном 3 и 10 МПа, допускаются радиусы изгиба, превышающие во всех случаях 200 — 500 мм. Более приемлемые результаты получены при E_Дl МПа. С уменьшением относительного шага происходит уменьшение ε_ОВ. При h/А=20 допустим изгиб с R/А=30 — 40. В этом случае напряжение в оптическом волокне складывается из двух примерно равных частей, определяемых изгибами самого волокна и растяжением (сжатием), создаваемым кабелем. Расчеты для Ед = 0,1 МПа показали, что в этом случае определяющую роль играют деформации изгиба самого волокна. Деформации, вызванные влиянием остальных элементов кабеля, в несколько раз меньше. Допустимый радиус изгиба достигает 20 мм при А =2,5 мм и h/А =20 — 40 или при А =5 мм и h/А =20 — 30. Сравнение данных, приведенных на рис. 4.14, показывает, что кабели с плотной укладкой жил требуют применения весьма мягкого дем пфера с Е_Д=0,1 — 1 МПа. Только в этом случае кабель может быть подвергнут изгибу с достаточно малым радиусом.

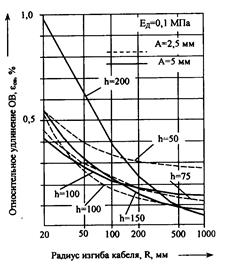
Рис. 4.14. Зависимость относительного удлинения оптического волокна при изгибе от величины радиуса

При воздействии на оптический кабель нескольких факторов напряжения в оптическом волокне в соответствующих точках суммируются.

Расчет деформации трубчатой полимерной оболочки при действии поперечной раздавливающей нагрузки. В процессе эксплуатации из-за внешних нагрузок и взаимодействия элементов ОК между собой возникают раздавливающие нагрузки, действующие на защитные покрытия ОВ и вызывающие их деформации. Если величины деформаций значительны, это может привести к существенным ухудшениям характеристик, а в некоторых случаях и к разрушению ОВ.

Для оценки степени деформации трубчатой полимерной оболочки ОВ с ТЗО (рис. 4.8 б) можно воспользоваться следующим выражением, полученным экспериментальным путем м.н.с. Кремезом А.С. (ВНИИКП):

(4.64)

где δ — изменение диаметра трубки по вертикальной оси; k — коэффициент, усредняющий результат вследствие перехода от упругой деформации полимера к пластической; G — коэффициент Пауссона, характеризующий соотношения между продольными и поперечными деформациями материала; R — средний диаметр трубки; h — радиальная толщина трубки; Е — модуль упругости материала трубки; q — линейная интенсивность нагрузки, равная отношению раздавливающей силы F и длины трубчатого покрытия l на участке действия этой силы, т.е. q=F/l.

Значения параметров в выражении (4.64) по литературным и экспериментальным данным для полимеров, используемых обычно в качестве ТЗО, определяются следующими величинами.

Коэффициент k = 14,6 ÷ 15,5, причем нижний предел соответствует оболочкам из ПВХ и ПЭНП, а верхний — из ФТ-2М.

Коэффициент G зависит только от природы материала и можно принять следующие его значения (полученные экспериментально): 0,4(ФТ-2М); 0,85(ПВХ); 0,7(ПЭНП).

Средние значениямодуляупругости Е: 120 кг/мм² (ФТ-2М),3,2кг/мм² (ПВХ),20кг/мм² (ПЭНП).

Расчет прочности армирующих элементов ОК. Остановимся на расчете прочности армирующих элементов ОК, расположенных концентрически на периферии или в центре ОК. Согласно [1, 2] разложим приложенную к армирующему элементу силу на составляющие (рис.4.15). Из рисунка видно, что

(4.65)

где F_пр1 — расчетное значение суммарного разрывного усилия армирующих элементов в повиве; S_А1 — суммарное сечение армирующих элементов в повиве; о;и — номинальное значение разрывной прочности армирующих элементов в повиве; σ_А1 — угол скрутки армирующих элементов в повиве.

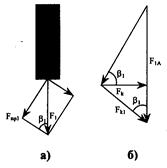
Рис.4.15. Усилия, возникающие в концентрически расположенных армирующих элементах (броне) оптического кабеля:

а – к расчету разрывной прочности армирующих элементов (брони);

б – к расчету крутящего момента оптического кабеля

При наличии нескольких повивов аналогично имеем силу, приложенную к i-му повиву в виде:

(4.66)

Суммарное разрывное усилие в кабеле:

(4.67)

Количество проволок в повиве может быть выбрано в соответствии с [12, 13].

В оптических кабелях, элементы которых расположены по спирали, при растяжении возникают крутящие моменты, которые стремятся раскрутить броню или армирующий элемент, что может привести к выходу кабеля из строя. Поэтому его конструкция должна быть разработана таким образом, чтобы суммарный крутящий момент был минимальным.

Рассмотрим действие растягивающей силы F₁ на один повив армирующего элемента (или брони), состоящий из п_А проволок (рис. 4.15 б). Сила F_1А, действующая на одну из проволок, определяется как

(4.68)

Сила F_k1 создает крутящий момент, стремящийся повернуть повив проволок. Проекцию F_k1 на направление, перпендикулярное оси кабеля, обозначим через F_k. Эта сила действует на плечо, равное R_A, где R_A — радиус повива армирующего элемента. Из рис. 4.15 б следует, что

F_k1= F_1Acosβ₁,

F_k1= F_1Asinβ₁= F_k1= F_1Acosβ₁sinβ₁=F_1Atgβ₁cos²β.

Принимая

(4.69)

где m — коэффициент скрутки,

и cos²β=1/(1+tg² β), получаем силу, действующую перпендикулярно оси ОК,

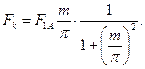(4.70)

Общий крутящий момент повива проволок при замене F_1A выражением (4.70):

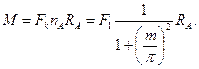(4.71)

Растягивающая сила на один повив может быть представлена в виде:

(4.72)

где d_А — диаметр проволоки.

Тогда для этого повива крутящий момент может быть выражен в виде:

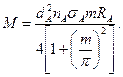(4.73)

Таким образом, величина крутящего момента при растягивающих нагрузках зависит от величины растягивающего усилия, конструкции армирующих элементов или брони и от параметров скрутки. Если пренебречь действием сил трения и внутренних сил упругости в кабеле, то условие равновесия крутящих моментов ∑М = 0 для двухповивной конструкции брони может быть обеспечено при

,

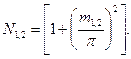(4.74)

Анализ этого уравнения показывает, что его решение возможно только при значительном уменьшении диаметра проволок второго повива [1, 2].