1.1. Предмет теории передачи сигналов
1.3. Сообщение и сигнал. Канал связи
1.5. Демодуляция и декодирование
1.1. Предмет теории передачи сигналов
Теория передачи сигналов — это наука о передаче информации на расстояние.
В настоящее время электрические сигналы применяются для передачи различных сообщений, и обнаружения объектов в пространстве, для автоматического управления промышленными объектами и космическими кораблями, для выполнения физических измерений и наблюдений, для решения математических задач с помощью электронных вычислительных машин и для многих других целей.
Современные проблемы в области теории и техники связи определяются новыми условиями и вытекающими из их новыми, более высокими требованиями. В первую очередь повышаются требования к скорости и достоверности передачи информации. Быстродействие и достоверность являются важнейшими характеристиками современных систем связи.
Процесс передачи информации по каналам связи всегда является вероятностным, поэтому в основе теории передачи сигналов лежат статистические методы исследований. Объектом статистических методов здесь являются не только помехи и шумы, но и сами полезные сигналы.
Курс теории передачи сигналов представляет собой единую научную дисциплину, основу которой составляют теория сигналов, теория помехоустойчивости и теория информации.
В курсе изучаются общие закономерности передачи информации по каналам связи, определяются потенциальные возможности различных способов передачи и приема сигналов, сравниваются различные системы связи между собой и определяются алгоритмы работы отдельных элементов системы связи.
Задача теории определить, как должен работать тот или иной элемент системы связи и каким требованиям он должен удовлетворять. Вопросы же о том, как рассчитать и построить эти элементы, изучаются в специальных инженерных курсах.
Начало общей теории передачи сообщений было заложено в работе В. А. Котельникова «О пропускной способности «эфира» и проволоки» (1933 г.), в который была сформулирована и доказана теорема отсчетов, и в работе Р. Хартли «Передача информации» (1928 г.), в которой была введена логарифмическая мера информации. Следующим крупным шагом в развитии теории явились фундаментальные работы В. А. Котельникова по теории потенциальной помехоустойчивости (1946 г.) и К. Шеннона по теории информации (1948 г.). В этих работах были сформулированы основные положения и теоремы современной теории передачи сообщений.
Дальнейшее развитие теория получила в трудах А. А. Харкевича, Д. В. Агеева, В. И. Сифорова, Д. Миддлтона и многих других советских и зарубежных ученых. Большое влияние на развитие теории оказали выдающиеся математики А. Н. Колмогоров, Н. Винер, А. Я. Хинчин и другие.
В нашей стране развитию теории и внедрению ее в практику придается большое значение. О высоком уровне советской науки и техники в области связи свидетельствуют такие достижения, как создание сложнейших систем управления космическими кораблями и ракетами, систем дальней и сверхдальней космической связи, систем связи и телевидения с использованием искусственных спутников Земли. В этих системах применяются наиболее совершенные способы передачи, оптимальные методы обработки сигналов ,и помехоустойчивые коды, позволяющие обнаруживать и исправлять ошибки, возникающие в канале. Создание подобных систем было бы невозможно без выдающихся успехов современной теории и техники связи.
1.2. Система связи
Объектом передачи в любой системе связи является сообщение, несущее какую-либо информацию. Сообщение может быть непрерывным (речь, музыка) или дискретным (письменный текст, цифровые данные).
Рис. 1.1. Функциональная схема системы связи
На рис. 1.1 приведена функциональная схема системы связи. Рассмотрим назначение отдельных элементов этой схемы. Источником информации является отправитель сообщения, а потребителем — ее получатель. В одних системах связи источником и потребителем информации может быть человек, в других — различного рода автоматические устройства, вычислительные машины и т. п.
Поступающее от источника сообщение u(t) в передатчике обрабатывается определенным образом, и формируется сигнал s(t), удобный для передачи по линии связи. В телефонии, например, эта операция сводится просто к преобразованию звукового давления в пропорционально изменяющийся электрический ток микрофона. В телеграфии производится кодирование, в результате которого последовательность элементов сообщения (букв, цифр) преобразовывается в последовательность кодовых символов (0, 1; точка, тире).
Линией связи называется среда, используемая для передачи сигналов от передатчика к приемнику. В системах электрической связи, в частности, это пара проводов, кабель или волновод, в системах радиосвязи — область пространства, в которой распространяются электромагнитные волны от передатчика к приемнику.
При передаче сигнал может искажаться и на него могут воздействовать помехи ω(t). Приемник обрабатывает принятый сигнал x(t), искаженный помехой, и восстанавливает по нему переданное сообщение u(t). Обычно в приемнике выполняются операции, обратные тем, которые были осуществлены в передатчике.
Каналом связи принято называть совокупность технических средств, служащих для передачи сообщения от источника к потребителю. Этими средствами являются передатчик, линия связи и приемник. Канал связи вместе с источником и потребителем образует систему связи. Различают системы передачи дискретных сообщений (например, система телеграфной связи) и системы передачи непрерывных сообщений (системы радиовещания, телевидения, телефонии и т. п.). Существуют также системы связи смешанного типа, в которых непрерывные сообщения передаются дискретными сигналами. К таким системам относятся, например, системы импульсно-кодовой модуляции.
Система связи называется многоканальной, если она обеспечивает взаимонезависимую передачу нескольких сообщений по одному общему каналу связи.
Система связи может служить не только для передачи информации от человека к человеку, но и для передачи результатов измерения параметров какого-нибудь (процесса или воздействий, предназначенных для управления объектом.
Система телеизмерения (телеметрии) подобна системе связи. В этой системе физическая величина, подлежащая измерению (температура, давление, скорость и т. п.), с помощью датчиков воздействует на передатчик, где она преобразовывается в сигнал и передается по каналу. На приемном конце переданная физическая величина или ее изменения выделяются из сигнала и наблюдаются, или регистрируются с помощью приборов. В системе телеуправления предусмотрено выполнение определенных действий в соответствии с измеряемой величиной. Для этой цели имеются регулирующие устройства и цепь обратной связи.
1.3. Сообщение и сигнал. Канал связи
Под информацией понимают сведения о каком-либо явлении, событии, объекте. Информация, выраженная b определенной форме, представляет собой сообщение, иначе говоря, сообщение — это то, что подлежит передаче. Сигнал является материальным носителем сообщения.
В качестве сигнала можно использовать любой физический процесс, изменяющийся в соответствии с переносимым сообщением. Существенно то, что сигналом является не сам физический процесс, а изменения отдельных параметров этого процесса. Указанные изменения определяются тем сообщением, которое несет данный сигнал. Правила этих изменений — код — обычно задаются заранее.
В системах связи сигнал предназначен для передачи информации от отправителя к получателю. Код полностью известен как на передающей, так и приемной сторонах — он устанавливается заранее.
Сообщения и соответствующие им сигналы бывают дискретными и непрерывными. Дискретное сообщение представляет собой последовательность отдельных элементов. Физическая природа этих элементов может быть любой. Сигнал в этом случае также представляет собой дискретную последовательность отдельных элементов, соответствующих элементам передаваемого сообщения. С дискретными сигналами мы встречаемся в цифровой вычислительной технике, в телеграфии. Так, гари передаче обычной телеграммы сообщением является теист телеграммы, элементами сообщения — буквы, сигналами — кодовые комбинации, соответствующие этим буквам.
Непрерывное сообщение — это некоторая физическая величина (звуковое давление, температура и т. п.), принимающая любые значения в заданном интервале. Сообщение с помощью датчиков преобразовывается в непрерывно изменяющуюся электрическую величину u(t) — видеосигнал. При передаче речи такое преобразование выполняет микрофон, а при передаче изображения — электронно-лучевая трубка. В большинстве случаев видеосигнал является низкочастотным колебанием, которое отображает передаваемое сообщение. Для удобства анализа видеосигнал часто условно рассматривают как сообщение, которое необходимо передать по каналу связи.
В некоторых случаях видеосигнал непосредственно передается по линии. Так поступают, например, при обычной городской телефонной связи. Для передачи на большие расстояния (по кабелю или радио) видеосигнал преобразовывается в высокочастотный сигнал (радиосигнал) (рис. 1.2).
Во многих случаях сигнал отображает временные процессы, происходящие в некоторой системе. Поэтому описанием конкретного сигнала может быть некоторая функция времени s(t). Определив так или иначе эту функцию, мы определяем и сигнал. Однако такое полное описание сигнала требуется не всегда. Для решения ряда вопросов достаточно более общего описания в виде нескольких обобщенных параметров, характеризующих основные свойства сигнала, подобно тому, как это делается в системах транспортирования.
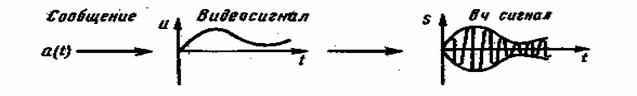
Рис. 1.2. Преобразование непрерывного сообщения в сигнал
Указывая габариты и вес, мы характеризуем основные свойства предмета с точки зрения условий его транспортирования; другие свойства (например, цвет) с этой точки зрения являются несущественными.
Сигнал есть также объект транспортирования, а техника связи есть, то существу, техника транспортирования (передачи) сигналов по каналам связи. Поэтому целесообразно определить параметры сигнала, которые являются основными с точки зрения его передачи. Такими параметрами являются длительность сигнала, его динамический диапазон и ширина спектра.
Всякий сигнал, рассматриваемый как временной процесс, имеет начало и конец. Поэтому длительность сигнала Т является естественным его параметром, определяющим интервал времени, в пределах которого сигнал существует.
Характеристиками сигнала внутри интервала его существования являются динамический диапазон и скорость изменения сигнала. Динамический диапазон определяется как отношение наибольшей мгновенной мощности сигнала к наименьшей. Динамический диапазон речи диктора, например, равен 25-30 дб, небольшого вокального ансамбля — 45-55 дб, симфонического оркестра — 65-75 дб.
В реальных условиях всегда имеют место помехи. Для удовлетворительной передачи требуется, чтобы наименьшая мощность сигнала превышала мощность помех. Отношение сигнала к помех характеризует относительный уровень сигнала. Обычно определяется логарифм этого отношения, который называется превышением сигнала над помехой. Это превышение и принимается в качестве второго параметра сигнала.
Третьим параметром является ширина спектра сигнала F. Эта величина даёт представление о скорости изменения сигнала внутри интервала его существования. Спектр сигнала может простираться в пределах очень большого диапазона частот. Однако для многих сигналов можно указать диапазон частот, в пределах которого сосредоточена его основная энергия. Этим диапазоном и определяется ширина спектра сигнала.
В технике связи спектр сигнала часто сознательно ограничивается. Это обусловлено тем, что аппаратура и линия связи имеют ограниченную полосу пропускаемых частот. Ограничение спектра осуществляется, исходя из допустимых искажений сигнала. Например, при телефонной связи требуется выполнить два условия: чтобы речь была разборчива и корреспонденты могли узнать друг друга по голосу. Для выполнения этих условий спектр речевого сигнала можно ограничить полосой от 300 до 3400 Гц. Передача более широкого спектра речи в этом случае нецелесообразна, так как это ведет к техническим усложнениям и увеличению затрат.
Второй пример. Необходимая ширина спектра телевизионного сигнала определяется требуемой четкостью изображения. При стандарте 625 строк, который принят в Советском Союзе, верхняя частота сигнала получается порядка 6 МГц. Спектр телевизионного сигнала много шире спектра звукового сигнала. Это существенно усложняет построение систем телевизионного вещания по сравнению с системами звукового вещания. Ширина спектра телеграфного сигнала зависит от скорости передачи и обычно принимается равной F
1,5 v, где v — скорость телеграфирования в бодах, определяющая количество переданных телеграфных посылок за единицу времени. Так, при телетайпной передаче v=50 бод и F=75гц.
Спектр модулированного сигнала обычно шире спектра передаваемого сообщения (видеосигнала) и зависит от вида модуляции Канал связи можно характеризовать так же, как и сигнал, третий параметрами: временем, в течение которого по каналу ведется передача, динамическим диапазоном и полосой пропускания канала. Типы каналов, по которым передаются сообщения, многочисленны и разнообразны. Широкое применение находят каналы проводной связи, коротковолновой радиосвязи с использованием отражения от ионосферы, ультракоротковолновой связи ионосферного и тропосферного рассеяния, метеорной связи, космической связи и т. п. Характеристики этих каналов значительно отличаются друг от друга.
Общими признаками различных каналов являются следующие. Во-первых, большинство каналов можно считать линейными. В таких каналах выходной сигнал представляет собой просто сумму входных сигналов (принцип суперпозиции). Во-вторых, на выходе канала даже при отсутствии полезного сигнала всегда имеются помехи. В- третьих, сигнал при передаче по каналу претерпевает задержку во времени и затухание по уровню. И, наконец, в реальных каналах всегда имеют место искажения сигнала, обусловленное несовершенством канала.
Сигнал на выходе канала можно записать в следующем виде:
x(t)=μs(t-τ)+ω(t), (1.1)
где s(t)— сигнал на входе канала, ω(t)— помеха, μ и τ — величины, характеризующие затухание и время задержки сигнала.
Канал, в котором μ и τ фиксированы во времени, называется каналом с постоянными параметрами. В реальных условиях проходит непрерывное и часто случайное изменение параметров μ и τ. Такие каналы называются каналами с переменными параметрами. Встречаются каналы, в которых сигнал в точку приема приходит по различным путям с различными затуханиями μ
и различными запаздываниями τ. Такие каналы называют многопутевыми или многолучевыми.
1.4. Кодирование и модуляция
Преобразование дискретного сообщения в сигнал состоит из двух операций: кодирования и модуляции. Кодирование определяет закон построения сигнала, а модуляция — вид формируемого сигнала, который должен передаваться по каналу связи.
Простейшим примером дискретного сообщения является текст. Любой текст состоит из конечного числа элементов: букв, цифр, знаков препинания. Для европейских языков число элементов колеблется от 52 до 55, для восточных языков оно может исчисляться сотнями и даже тысячами. Так как число элементов в дискретном сообщении конечно, то их можно пронумеровать и тем самым свести передачу сообщения к передаче последовательности чисел.
Так, для передачи букв русского алфавита (их 32) необходимо передавать числа от 1 до 32. Для передачи любого числа, записанного в десятичной форме, требуется передача десяти цифр от 0 до 9. Практически для этого нужно передавать по каналу связи десять сигналов, соответствующих различным шифрам. Систему передачи дискретных сообщений можно существенно упростить, если воспользоваться при кодировании двоичной системой счисления.
В десятичной системе основанием счисления является число 10. Поэтому любое число N можно представить в виде
N
(1.2)
где 
,— коэффициенты, принимающие значения от 0 до 9. Так, число 265 можно записать как 
. Очевидно, в качестве основания счисления можно принять любое целое число т и представить число N как 
(1.3)
где коэффициенты, принимающие значение от 0 до m-1.
Задаваясь величиной т, можно построить любую систему счисления. При т=2 .получим двоичную систему, в которой числа записываются при помощи всего лишь двух цифр: 0 и 1. Например, число 13 в двоичной системе записывается 1101, что соответствует выражению 
. Арифметические действия в двоичной системе весьма простые. Так, сложение осуществляется по следующим правилам: 0+0=0;0+1=1;1+0=1;1+1=10. Различают еще символическое поразрядное сложение без переноса в высший разряд, так называемое «сложение по модулю два». Правила этого сложения следующие: 0
0=0;01=1;10=1;11=0;
Если преобразовать последовательность элементов сообщения в последовательность двоичных чисел, то для передачи последних по каналу связи достаточно передавать всего лишь два кодовых символа: 0 и 1. Практическая реализация такой передачи весьма простая. Например, символы 0 и 1 могут передаваться колебаниями с различными частотами или посылками постоянного тока равной полярности. Благодаря своей простоте двоичная систему счисления нашла широкое применение при кодировании дискретных сообщений.
При кодировании происходит процесс преобразования элементов сообщения в соответствующие им числа (кодовые символы). Каждому элементу сообщения присваивается определенная совокупность кодовых символов, которая называется кодовой комбинацией. Совокупность кодовых комбинаций, обозначающих дискретные сообщения, называется кодом. Правило кодирования обычно выражается кодовой таблицей, в которой приводятся алфавит кодируемых сообщений и соответствующие им кодовые комбинации (см. табл. l.l и l.2). Множество возможных кодовых символов
Таблица 11 Таблица 12
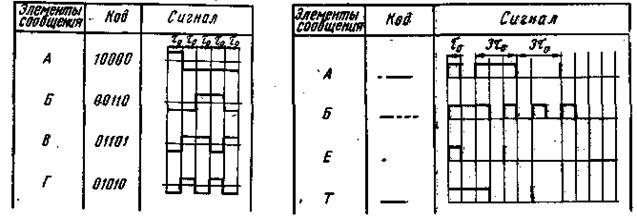
называется кодовым алфавитом, а их количество – основанием кода. В общем случае при основании, когда m правила кодирования N элементов сообщения сходятся к правилам записи N различных чисел в m-ичной системе счисления. Число символов n, образующих кодовую комбинацию, называется значность кода, или длиной кодовой комбинации.
В зависимости от системы счисления, используемой при кодировании, различают двухпозиционные и многопозиционные коды. К первым относятся все коды, в которых используется двоичная система счисления. Часто эти коды называют двоичными. К многопозиционным кодам относятся все коды, в которых число позиций (основание кода) больше двух. Различают коды равномерные и неравномерные.
Равномерными называют такие коды, у которых все кодовые комбинации имеют одинаковую длину. Для равномерного кода число возможных кодовых комбинаций равно тп. Примером такого кода является пятизначный код Бодо. Этот код содержит пять двоичных элементов (т = 2, n = 5). Число возможных кодовых комбинаций равно 25 = 32, что достаточно для кодирования всех букв алфавита. В табл. 1.1 приведено несколько кодовых комбинаций кода Бодо для случая, когда символ 1 передается положительным импульсом длительности τ
, а символ 0 — отрицательным импульсом той же длительности. Время передачи любой кодовой комбинации равно 5τ. Применение равномерных кодов упрощает построение автоматических буквопечатающих устройств и не требует передачи разделительных символов между кодовыми комбинациями.
Неравномерные коды характерны тем, что у них кодовые комбинации отличаются друг от друга не только взаимным расположением символов 0 и 1, но и их количеством. Это приводит к тому, что различные кодовые комбинации имеют разную длительность.
Типичным примером неравномерных кодов является код Морзе, в котором символы 0 и 1 используются только в двух сочетаниях: как одиночные (1 и 0) или как тройные (111 и 000). Сигнал, соответствующий одной единице, называется точкой, трем единицам — тире. Символ 0 используется как знак, отделяющий точку от тире, точку от точки и тире от тире. Совокупность 000 используется как разделительный знак между кодовыми комбинациями. Изложенный принцип построения кода поясняется табл. 1.2, в которой приведено несколько кодовых комбинаций для случая передачи однополярными импульсами. Из таблицы видно, что время передачи различных кодовых комбинаций неодинаково. Самая короткая кодовая комбинация (буква «Е») по длительности равна 4 τ, а самая длинная (цифра 0) —22τ. Средняя длительность кодовой комбинации при передаче твиста на русском языке равна примерно 9,5τ. По сравнению с пятизначным равномерным кодом Бодо это почти в два раза больше.
По помехоустойчивости коды делятся на обыкновенные и корректирующие. Коды, у которых все возможные кодовые комбинации используются для передачи информации, называются обыкновенными или кодами без избыточности. В обыкновенных равномерных кодах превращение одного символа комбинации в другой, например 1 в 0 или 0 в 1, приводит к появлению новой возможной комбинации, т. е. к ошибке.
Корректирующие коды строятся так, что для передачи сообщения используются не все возможные кодовые комбинации, а лишь некоторая их часть. Тем самым создается возможность обнаружить и поправлять ошибки при неправильном воспроизведении некоторого числа символов.
Рис. 1.3. Функциональная схема системы передачи дискретных сообщений
Корректирующие свойства кодов достигаются ценой введения в кодовые комбинации дополнительных (избыточных) символов.
Декодирование состоит в восстановлении сообщения по принимаемым кодовым символам. Устройства, осуществляющие кодирование и декодирование, называются соответственно кодером и декодером. Как правило, это нелинейные логические устройства. На рис. 1.3 изображена функциональная схема системы передачи дискретных сообщений, а на рис. 1.4 и 1.5 поясняются процесс преобразования дискретного сообщения в сигнал и обратно, преобразование принятого сигнала в сообщение.
Рис. 1.4. Процесс преобразования дискретного сообщения в сигнал
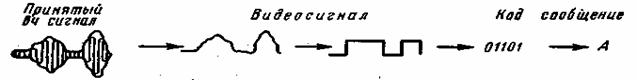
Рис. 1.5. Процесс восстановления переданного сообщения в приемнике
Передача сообщений по каналу связи осуществляется с помощью некоторого физического процесса, который называется переносчиком. В электросвязи таким переносчикам является электрическое колебание.
Всякий сигнал — будь то сигнал телеграфный, телефонный или любой другой — получается путем модуляции. Немодулированный переносчик не несет информации — он подобен чистому листу бумаги, в то время как модулированный переносчик можно сравнить с листом бумаги, на котором написаны буквы, знаки, отображающие ту или иную информацию.
Модуляция состоит в том, что один из параметров переносчика f(a,b,c,…) изменяется во времени в соответствии с передаваемым сообщением u(t), например,
(1.4)
где т =
— коэффициент модуляции.
Если изменяется (модулируется) параметр с, то имеем c-модуляцию, если изменяется параметр b, то имеемb-модуляцию и т. д. Модулированные сигналы различаются переносчиками и модулируемыми параметрами. Число возможных видов модуляции при данном виде переносчика определяется числом его параметров.
При передаче сообщений на большие расстояния переносчиком обычно является синусоидальное колебание высокой частоты
f(t)=
(1.5)
Параметрами этого колебания являются амплитуда А, частота ω и фаза φ. Каждый из этих параметров можно модулировать и получить соответственно: амплитудную модуляцию (AM), частотную модуляцию (ЧМ) и фазовую модуляцию (ФМ). При этом данный параметр переносчика имеет приращение, пропорциональное u(t). Так,
при AM A=
(1.6)
при ФМ 
(1.7)
при ЧМ 
(1.8)
Если сообщение закодировано двоичным кодом, то модулируемый параметр будет принимать только два значения: одно будет соответствовать передаче символа 1, другое — передаче символа 0. В этом случае модуляцию называют манипуляцией.
В современных системах связи, особенно в многоканальных, в качестве переносчика часто используется периодическая последовательность импульсов определенной формы. Параметрами такой последовательности являются амплитуда импульсов, длительность, их положение во времени (фаза) и частота следования. Это позволяет получить четыре основных вида импульсной модуляции: амплитудно-импульсную модуляцию (АИМ), широтно-импульсную модуляцию (ШИМ), фазо-импульсную модуляцию (ФИМ) и частотно-импульсную (ЧИМ).
В системах радиосвязи термин «импульсная модуляция», по существу, означает двойную модуляцию: первичную модуляцию последовательности импульсов передаваемым сообщением и вторичную модуляцию высокочастотного синусоидального колебания напряжением, получаемым в результате первичной модуляции. При этом во второй ступени модуляции используются рассмотренные выше способы модуляции синусоидального переносчика (AM, ЧМ, ФМ). В результате получается целый ряд систем с импульсной модуляцией: АИМ- AM, ФИМ-АМ, ШИМ-ЧМ, ШИМ-ФМ и т. д.
В некоторых случаях модулирующее сообщение воздействует одновременно не на один, а на несколько параметров. Такую модуляцию называют смешанной. Возможны, например, амплитудно-частотная, амплитудно-фазовая модуляции и т. п.
1.5. Демодуляция и декодирование
Восстановление переданного сообщения в приемнике обычно осуществляется в такой последовательности. Сначала производится детектирование сигнала. Цель этой операции состоит в извлечении из модулированного сигнала колебания модулирующей частоты. При этом производятся действия, обратные операции модуляции, поэтому детектирование часто называют демодуляцией. Демодуляция, так же как и модуляция, процесс, существенно нелинейный и поэтому практически осуществляется с помощью нелинейных или параметрических устройств.
В системах передачи непрерывных сообщений в результате демодуляции выделяется видеосигнал, отображающий переданное сообщение. Этот сигнал затем поступает, на воспроизводящее или записывающее устройство. В радиовещании таким устройством может быть громкоговоритель или магнитофон.
В системах передачи дискретных сообщений в результате демодуляции последовательность элементов сигнала превращается в последовательность кодовых символов, после чего эта последовательность преобразовывается в (последовательность элементов сообщения, выдаваемую получателю (рис. 1.5). Это преобразование называется декодированием.
Иногда операции демодуляции и декодирования объединяются в одном устройстве, которое приходящую последовательность элементов сигнала преобразовывает сразу в последовательность букв сообщения. Такой метод приема называют «приемом в целом», в отличие от широко распространенного метода «поэлементнoгo приема». В первом случае анализируется целиком отрезок сигнала, соответствующий кодовой комбинации, и на основании того или иного критерия восстанавливается переданный элемент сообщения (буква). Во втором случае сначала анализируются отдельные элементы сигнала, соответствующие кодовым символам, а затем восстановленная кодовая комбинация декодируется, т. е. преобразовывается в элемент (букву) сообщения.
Строго говоря, по принятому сигналу можно судить лишь с некоторой степенью точности о том, что был передан тот или иной сигнал из множества возможных для данной системы сигналов. При этом необходимо решить , какому переданному сигналу соответствует принятый сигнал. В некоторых случаях это решение принимает сам человек. Так, например, при приеме телеграфных сигналов на слух оператор решает, какой сигнал («точка» или «тире») был передан. Он же выполняет и операцию декодирования.
В приемниках дискретных сообщений, предназначенных для записи информации, все эти операции выполняются автоматически. В этих случаях приемник принимает решение, какому переданному сигналу соответствует принятый искаженный сигнал. Для этой цели сигнал сначала детектируется, а затем опознается с помощью решающей схемы. Демодулятор при этом состоит из детектора и решающего устройства.
В простейшем случае решающая схема представляет собой пороговое устройство в форме реле или триггера, работающих по принципу «да» или «нет». Если принятый элемент сигнала имеет значение выше порогового, выдается один символ кода, например, (1), если ниже — другой (0). Высота порога, очевидно, должна выбираться с учетом вероятности появления элементов сигнала и относительной важности положительного и отрицательного решений.
В более ответственных случаях применяются решающие схемы с двумя порогами. В этом случае при попадании уровня сигнала между двумя порогами решение не принимается — вместо сомнительного элемента сигнала выдается специальный символ стирания. Введение такого стирающего символа облегчает возможность правильного декодирования принятой кодовой комбинации.
1.6. Дискретизация и кодирование непрерывных сообщений
Под дискретизацией понимается преобразование непрерывных сообщений (сигналов) в дискретные. При этом используется дискретизация по времени и по уровню.
Дискретизация по времени выполняется путем взятия отсчетов функции u(t) в определенные дискретные моменты времени t
. В результате непрерывная функция u(t) заменяется совокупностью мгновенных значений и={u(t)}. Обычно моменты отсчетов выбираются на оси времени равномерно, т. е. t=
. Выбор интервала Δt производится на основании теоремы Котельникова, согласно которой функция с ограниченным спектром полностью определяется своими значениями, отсчитываемыми через интервалы Δt=1/2F, где F — ширина спектра. Дискретизация по времени лежит в основе всех видов импульсной модуляции.
В некоторых случаях сообщение может представлять собой функцию не одного, а нескольких переменных. Примером такого сообщения является телевизионное изображение, которое можно представить как функцию и(х, у, t) двух пространственных координат х и у и времени t, где и — яркость изображения. Дискретизация по времени осуществляется с помощью кадровой развертки. Шаг дискретизации Δt равен числу кадров в секунду. В результате строчной развертки дискретизируется координата у, координата х при этом остается непрерывной. Шаг дискретизации Δy определяется числом строк развертки. Таким образом, получается функция
u(t)=u(iΔy,kΔt,vt),
где v— скорость развертки вдоль строки, i — номер строки, k — номер кадра.
Дискретизация значений функции (уровня) носит название квантования. Операция квантования сводится к тому, что вместо данного мгновенного значения сообщений u(t) передаются ближайшие значения по установленной шкале дискретных уровней (рис. 1.6).
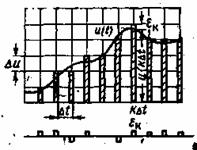
Рис.1.6 Дискредитизация непрерывной функции.
Дискретные значения по шкале уровней чаще всего выпираются равномерно: u=kΔu. Само собой разумеется, что при квантовании вносится погрешность (искажения), так как истинные значения функции и заменяются округленными значениями u. Величина этой погрешности ε=u-u не превосходит половины шага квантования Δu может быть сведена до допустимого значения. Погрешность ε является случайной функцией и проявляется на выходе как дополнительный шум («шум квантования»), наложенный на передаваемое сообщение.
Дискретизация одновременно по времени и уровню позволяет непрерывное сообщение преобразовать в дискретное, которое затем может быть закодировано и передано методами дискретной техники. Достоинствами систем связи с дискретизацией являются возможность применения кодирования для повышения помехоустойчивости, удобства обработки сигналов и сопряжения устройств связи с цифровыми вычислительными машинами.
В настоящее время из таких систем наибольшее применение находит система с импульсно-кодовой модуляцией (ИКМ). В этой системе непрерывное сообщение сначала подвергается дискретизации по времени и уровню, а затем полученная последовательность L уровней кодируется (чаще двоичным кодом). При этом каждому уровню присваивается кодовая комбинация, состоящая из п символов «1» и «0». Число символов п в кодовой комбинаций должно удовлетворять условию 
или 
. Полуденные кодовые комбинации могут передаваться по каналу связи любым методом дискретной модуляции. Обычно используются, частотная манипуляция (КИМ-ЧМ) или фазовая (КИМ-ФМ, КИМ-ОФМ).
В приемнике кодовые группы декодируются и образуют последовательность импульсов, величина которых пропорциональна переданным уровням квантования. В результате прохождения этих импульсов через фильтр нижних частот восстанавливается переданное непрерывное сообщение u(t).
Более простой метод преобразования непрерывного сообщения в дискретное осуществляется с помощью дельта-модуляции. При этом способе в начале каждого такта производится сравнение значения функции u(t) с предыдущим отсчетом и передается только знак приращения передаваемого сообщения u(t). Подробно кодовые способы модуляции рассматриваются в гл. 9.
1.7. Помехи и искажения
Общие сведения. В реальном канале сигнал при передаче искажается и сообщение воспроизводится с некоторой ошибкой. Причиной таких ошибок являются искажения, вносимые самим каналом, и помехи, воздействующие на сигнал.
Частотные и временные характеристики канала определяют так называемые линейные искажения. Кроме того, канал может вносить и нелинейные искажения, обусловленные нелинейностью тех или иных его звеньев. Как линейные, гак и нелинейные искажения обусловлены известными характеристиками канала и поэтому, в принципе, могут быть устранены путем надлежащей коррекции.
Следует четко отделить искажения от помех, имеющих случайный характер. Помехи заранее неизвестны и поэтому не могут быть полностью устранены.
Под помехой понимается любое воздействие, накладывающееся на полезный сигнал и затрудняющее его прием. Помехи весьма разнообразны как по своему происхождению, так и по физическим свойствам. В радиоканалах наиболее распространенными являются атмосферные помехи, обусловленные электрическими процессами в атмосфере и, прежде всего, грозовыми разрядами. Энергия этих помех сосредоточена, главным образом, в области длинных и средних волн. Сильные помехи создаются также промышленными установками. Это так называемые индустриальные помехи, возникающие из-за резких изменений тока в электрических цепях всевозможных электроустройств. Сюда относятся помехи от электротранспорта, электрических моторов, медицинских установок, систем зажигания двигателей и т. п.
Распространенным видом помех являются помехи от посторонних радиостанций и каналов. Этот вид помех обусловлен нарушением регламента распределения рабочих частот, недостаточной стабильностью частот, и плохой фильтрацией гармоник сигнала, а также нелинейными процессами в каналах, ведущими к перекрестным искажениям.
В проводных каналах связи основным видом помех являются импульсные шумы и прерывания связи. Появление импульсных помех часто связано с автоматической коммутацией и с перекрестными наводками. Прерывание связи есть явление, при котором сигнал в линии резко затухает или совсем исчезает. Такие прерывания могут быть вызваны различными причинами, из которых наиболее частыми являются нарушение контактов в реле, разъемах и т.п.
Практически в любом диапазоне частот имеют место внутренние шумы аппаратуры, обусловленные хаотическим движением носителей заряда в усилительных приборах, сопротивлениях и других элементах аппаратуры. Этот вид помех особенно сказывается в диапазоне ультракоротких волн. В этом диапазоне имеют значение и космические помехи, связанные с электромагнитными процессами, происходящими на Солнце, звездах и других внеземных объектах.
В общем виде влияние помехи ω на передаваемый сигнал s можно выразить оператором
x=Ψ(s,ω) (1.9)
В частном случае, когда оператор Ψ вырождается в сумм
x=s+ω (1.10)
помеха называется аддитивной. Если же оператор может быть представлен в виде произведения
x=μs (1.11)
то помеху называют мультипликативной. Здесь μ(t)— случайный процесс. Если μ— медленный по сравнению с сигналом процесс, то его называют замираниями. В реальных каналах обычно имеют место и аддитивные, и мультипликативные помехи, поэтому
x=μs+ω (1.12)
Флуктуационная помеха. Среди аддитивных помех особое место занимает флуктуационная помеха, которая является случайным процессом с нормальным распределением (гауссов процесс). Такая помеха наиболее изучена и представляет наибольший интерес, как в теоретическом, так и в практическом отношениях. Этот вид помех практически имеет место во всех реальных каналах. Сумма большого числа любых помех от различных источников также имеет характер флуктуационной помехи. И, наконец, многие помехи три прохождении через приемное устройство часто приобретают свойства нормальной флуктуационной помехи.
Электрическую структуру флуктуационной помехи можно представить себе как последовательность бесконечно коротких импульсов, имеющих случайную амплитуду и следующих друг за другом через случайные промежутки времени. При этом импульсы появляются один за другим настолько часто, что переходные явления в приемнике от отдельных импульсов накладываются, образуя непрерывный случайный процесс.
С физической точки зрения случайные помехи порождаются различного рода флуктуациями, т. е. случайными отклонениями тех или иных физических величин от их средних значений. Так, источником шума в электрических цепях могут быть флуктуации тока, обусловленные дискретной природой носителей заряда (электронов, ионов). Дискретная природа электрического тока проявляется в электронных лампах и полупроводниковых приборах в виде дробового эффекта.
Наиболее распространенной причиной шума являются флуктуации, обусловленные тепловым движением. Случайное тепловое движение носителей заряда в любом проводнике вызывает случайную разность потенциалов (напряжение) на его концах. Среднее значение напряжения равно нулю, а переменная составляющая проявляется как шум. Квадрат эффективного напряжения теплового шума определяется известной формулой Найквиста
(1.13)
где Т— абсолютная температура, которую имеет сопротивление R; F — полоса частот; k=
вт. сек/град— постоянная Больцмана.
Длительность импульсов, составляющих флуктуационную помеху, очень мала, поэтому спектральная плотность помехи постоянна вплоть до очень высоких частот. Типичным примером флуктуационных помех являются внутренние шумы приемника. Флуктуационный характер имеют космические помехи, а также некоторые виды атмосферных и индустриальных помех.
Импульсные помехи. К импульсным или сосредоточенным по времени помехам относят помехи в виде одиночных импульсов, следующих один за другим через такие большие промежутки времени, что переходные явления в радиоприемнике от одного импульса успевают практически затухнуть к моменту прихода следующего импульса. К таким помехам относятся многие виды атмосферных и индустриальных помех. Заметим, что понятия «флуктуационная помеха» и «импульсная помеха» являются относительными. В зависимости от частоты следования импульсов одна и та же помеха может воздействовать как импульсная на приемник с широкой полосой пропускания и как флуктуационная на приемник с относительно узкой полосой пропускания.
Импульсные помехи представляют собой дискретный случайный процесс, состоящий из отдельных редких, случайно распределенных по времени и амплитуде импульсов. Статические свойства таких помех с достаточной для практических целей полнотой описываются распределением вероятностей амплитуд импульсов и распределением временных интервалов между этими импульсами.
Сосредоточенные по спектру помехи. К этому виду помех принято относить сигналы посторонних радиостанций, излучения генераторов высокой частоты различного назначения (промышленные, медицинские) и т. п. Обычно это модулированные колебания, т. е. синусоидальные колебания с изменяющимися параметрами. В одних случаях эти колебания являются непрерывными (например, сигналы вещательных и телевизионных радиостанций), в других случаях они носят импульсный характер (сигналы радиотелеграфных станций). В отличие от флуктуационных и импульсных помех, спектр которых заполняет всю полосу частот приемника, ширина спектра сосредоточенной полежи в большинстве случаев меньше полосы пропускания приемника. В диапазоне коротких волн этот вид помех является основным, определяющим помехоустойчивость связи.
1.8. Достоверность и скорость передачи
Когда мы оцениваем работу системы связи, то прежде всего интересуемся, какую достоверность передачи сообщений обеспечивает система и сколько информации при этом передается. Первое определяет качество передачи, второе — количество.
В реальной системе связи достоверность передачи определяется степенью искажения сигнала. Эти искажения зависят от свойств и технического состояния системы, а также от интенсивности и характера помех. В правильно спроектированной и технически исправной системе связи искажения сигналов обусловлены лишь воздействием помех. В этом случае достоверность передачи сообщений полностью определяется помехоустойчивостью системы.
Под помехоустойчивостью обычно понимают способность системы противостоять вредному влиянию помехи на передачу сообщений. Так как действие помехи проявляется в том, что принятое сообщение отличается от переданного, то количественно помехоустойчивость при заданной помехе можно характеризовать степенью соответствия принятого сообщения переданному. Назовем эту величину общим термином — достоверность. Количественную меру достоверности приходится выбирать по-разному, в зависимости от характера сообщения.
Пусть сообщение представляет собой дискретную последовательность элементов из некоторого конечного множества возможных элементов. Влияние помехи на передачу такого сообщения проявляется в том, что вместо фактически переданного элемента может быть принят какой-либо другой. Такое событие называется ошибкой. В качестве количественной меры достоверности можно принять вероятность ошибки Р0 или любую возрастающую функцию этой вероятности.
При передаче непрерывных сообщений степенью соответствия принятого сообщения v(t) переданному u(t) может служить некоторая величина ε, представляющая собой отклонение v от и. Часто принимается критерий квадратичного уклонения, выражающийся соотношением
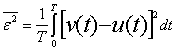(1.14)
Количественную меру достоверности можно также определить как вероятность того, что уклонение ε не превзойдет некоторой заранее заданной величины ε
:
(1.15)
Следует отметить, что достоверность передачи зависит от отношения мощностей сигнала к помехе. Чем больше это отношение, тем меньше вероятность ошибки (больше достоверность).
При дайной интенсивности помехи вероятность ошибки тем меньше, чем сильнее различаются между собой сигналы, соответствующие разным элементам сообщения. Задача состоит в том, чтобы выбрать для передачи сигналы с большим различием. Так, при фазовой манипуляции различие между сигналами больше, чем при амплитудной или частотной манипуляции. Поэтому следует ожидать, что достоверность передачи при ФМ будет выше, чем при AM и ЧМ.
Наконец, достоверность зависит и от способа приема. Нужно выбрать такой способ приема, который наилучшим образом реализует различие между сигналами при данном отношении сигнала к помехе. Правильно сконструированный приемник может увеличить отношение сигнала к помехе и притом весьма значительно.
Необходимо обратить внимание на существенное различие между системами передачи дискретных и непрерывных сообщений. В системах передачи непрерывных сообщений всякое, даже сколь угодно малое мешающее воздействие на сигнал, вызывающее искажение модулируемого параметра, всегда влечет за собой внесение соответствующей ошибки в передаваемое сообщение. В системах передачи дискретных сообщений ошибка возникает только тогда, когда сигнал воспроизводится (опознается) неправильно, а это происходит лишь при сравнительно больших искажениях. Свойство систем передачи дискретных сообщений правильно регистрировать искаженные (в некоторых пределах) сигналы называется справляющей способностью.
В теории помехоустойчивости, разработанной В. А. Котельниковым [4], показывается, что при заданном методе кодирования и модуляции существует предельная (потенциальная) помехоустойчивость, которая в реальном приемнике может быть достигнута, но не может быть превзойдена. Приемное устройство, реализующее потенциальную помехоустойчивость, называется оптимальным приемником.
Наряду с достоверностью (помехоустойчивостью) важнейшим показателем работы системы связи является скорость передачи. В системах передачи дискретных сообщений скорость измеряется числом передаваемых двоичных символов в секунду R. Для одного канала двоичная скорость передачи определяется соотношением
(1.16)
где τ— длительность элементарной посылки сигнала, m— основание кода. При m=2, R=1/τ.
Для любого канала при заданных ограничениях существует предельная скорость передачи, которая называется пропускной способностью канала С. В реальных системах скорость передачи всегда меньше пропускной способности канала С.
Современная теория показывает, что при R
C можно найти такие способы передачи и соответствующие им способы приема, при которых достоверность передачи может быть сделана сколь угодно большой [13].
Вопросы для повторения
1. Объясните принцип передачи непрерывных сообщений на примере телефонной связи.
2. Объясните принцип телеграфной связи.
3. Дайте определение сообщения, сигнала и помехи. Что такое видеосигнал?
4. Что называется каналом связи? Какие типы каналов Вы знаете?
5. Что называется кодовой комбинацией, основанием кода, длиной кодовой комбинации?
6. Приведите примеры равномерного и неравномерного кодов.
7. Объясните основные виды модуляции синусоидального переносчика?
8. Поясните принцип демодуляции в аналоговых системах.
9. Как осуществляются демодуляция и декодирование в системах передачи дискретных сообщений?
10. Что называется решающим устройством? Приведите пример простейшего РУ.
11. Поясните принцип дискретизации и кодирования непрерывных сигналов.
12. Чем отличаются помехи от искажений?
13. Дайте определение флуктуационной, сосредоточенной и импульсной помех.
14. Какие помехи называются аддитивными и какие — мультипликативными. Приведите примеры тех и других.
15. Что такое достоверность передачи и как она определяется количественно?
16. Как определяется количественно скорость передачи информации?