В связи с развитием систем передачи цифровых сообщений возникла необходимость изучения дискретных случайных процессов. Ниже будут рассмотрены два вида таких процессов, а именно случайный и синхронный телеграфные сигналы.

Случайным телеграфным сигналом называют процесс, реализации которого принимают значения и , причем смены знака происходят в случайные моменты времени. Такой процесс наблюдается на выходе усилителя – ограничителя с порогами ограничения и при поступлении на его вход нормального случайного процесса.

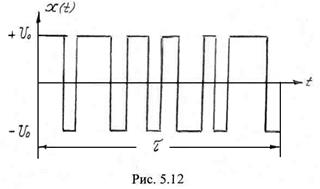На рис. 5.12 изображена реализация случайного телеграфного сигнала. Для случайного телеграфного сигнала число смены знака за время представляет собой дискретную случайную величину, распределенную по закону Пуассона

, (5.104)

где – интенсивность, т.е. число смены знака за единицу времени.

Найдем автокорреляционную функцию и энергетический спектр случайного телеграфного сигнала. В первую очередь отметим, что математическое ожидание случайного телеграфного сигнала . Автокорреляционная функция определяется усреднением произведения , т.е.

,

где черта означает операцию усреднения.

Это произведение принимает значение либо , если число смены знаков за время будет четным, либо , если число смены знаков будет нечетным. Так как вероятность числа смены знаков определяется законом Пуассона, то

.

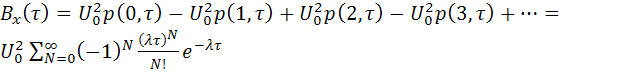Сумма сходящегося бесконечного ряда

.

Отсюда АКФ случайного телеграфного сигнала

, при .

С учетом того, что можно окончательно записать

. (5.105)

Односторонний энергетический спектр вычисляется в соответствии с теоремой Винера–Хинчина

.

Подстановка в это выражение соотношения (5.105) при , дает

. (5.106)

При вычислении (5.106) был использован табличный интеграл:

.

Синхронный телеграфный сигнал характеризуется тем, что смена знака сигнала происходит в строго определенные моменты времени, кратные длительности импульса τ_и. На рис. 5.13 изображена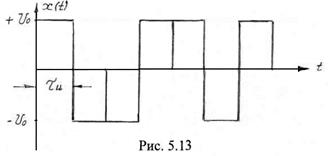

реализация синхронного телеграфного сигнала. Таким образом, синхронный телеграфный сигнал представляет собой случайную последовательность разнополярных прямоугольных импульсов длительностью .

Автокорреляционная функция синхронного телеграфного сигнала описывается выражением

, (5.107)

а энергетический спектр, вычисленный в соответствии с теоремой Винера–Хинчина

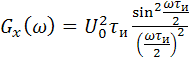. (5.108)

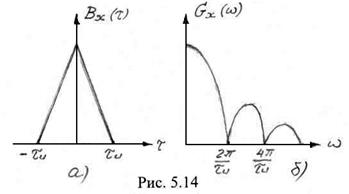
На рис. 5.14 изображены автокорреляционная функция и энергетический спектр синхронного телеграфного сигнала. Здесь прослеживается аналогия характеристик синхронного телеграфного сигнала и периодической последовательности разнополярных импульсов (последовательность вида «меандр»). Вместе с тем, если автокорреляционная функция периодической последовательности тоже периодична, то у синхронного телеграфного сигнала это свойство отсутствует.

В заключении отметим, что моделью синхронного телеграфного сигнала может быть описана последовательность кодовых комбинаций при передаче цифровых сигналов.