На рис. 15.1 представлен обзор проявления эффектов замирания в каналах. Он начинается с двух типов эффектов замирания, характерных для мобильной связи: крупномасштабное и мелкомасштабное замирание. Крупномасштабное замирание отражает среднее ослабление мощности сигнала или потери в тракте вследствие распространения на большое расстояние. На рис. 15.1 проявления крупномасштабного замирания показаны в блоках 1-3. На это явление влияют выступающие наземные элементы (например холмы, леса, рекламные щиты, группы строений и т.д.) между передатчиком и приемником. Часто говорят, что приемник "затеняется" этими выступами. Статистика крупномасштабного замирания позволяет приблизительно рассчитать потери в тракте как функцию расстояния. Это часто описывается через средние потери в тракте (степенной закон п-го порядка) и логарифмически нормально распределенные отклонения от среднего. Мелкомасштабное замирание — это значительные изменения амплитуды и фазы сигнала, которые на практике могут быть результатом небольших изменений (порядка половины длины волны) расстояния между передатчиком и приемником. Как указано на рис. 15.1 (блоки 4-6), мелкомасштабное замирание проявляется двумя способами — расширение сигнала во времени (или дисперсия сигнала) и нестационарное поведение канала. В мобильной радиосвязи параметры каналов изменяются во времени, поскольку движение передатчика и/или приемника приводит в результате к изменению пути распространения. Скорость изменения таких условий распространения определяет скорость замирания (скорость изменения ухудшения характеристик вследствие замирания). Мелкомасштабное замирание называется релеевским, если имеется большое число многократно отражающихся путей и нет компонента сигнала вдоль луча обзора; огибающая такого полученного сигнала статистически описывается с помощью релеевской функции плотности вероятности. Если преобладает незамирающий компонент сигнала, такой как путь распространения вдоль луча обзора, огибающая мелкомасштабного замирания описывается функцией плотности вероятности Раиса [1]. Иными словами, статистики мелкомасштабного замирания всегда распределены по Релею, если путь распространения вдоль луча обзора блокирован, в противном случае имеем распределение Раиса. Мобильный радиоприемник, который перемещается по большому пространству, должен иметь возможность обрабатывать сигналы, подвергнувшиеся замиранию обоих типов (мелкомасштабное, наложенное на крупномасштабное).

Крупномасштабное замирание (ослабление или потери в тракте) можно рассматривать как пространственное усреднение мелкомасштабных флуктуаций сигнала. Оно вычисляется, как правило, путем усреднения полученного сигнала по интервалу, превышающему 10-30 длин волн, чтобы отделить мелкомасштабные (главным образом релеевские) флуктуации от крупномасштабных эффектов затенения (обычно с логарифмически нормальным распределением). Существует три основных механизма, воздействующих на распространение сигнала в системах мобильной связи [1].

• Отражение (reflection) происходит тогда, когда распространяющаяся электромагнитная волна сталкивается с гладкой поверхностью, размер которой гораздо больше длины волны радиочастотного сигнала ().

• Дифракция (diffraction) встречается тогда, когда путь распространения между передатчиком и приемником преграждается плотным телом, размеры которого велики по сравнению с , что вызывает появление вторичных волн, образующихся позади преграждающего тела. Дифракция — это явление, которое является причиной того, что распространение радиочастотной энергии от передатчика к приемнику происходит в обход пути прямой видимости между ними. Ее часто называют затенением (shadowing), поскольку дифрагированное поле может достичь приемника, даже если оно затенено непроницаемой преградой.

• Рассеяние (scattering) встречается тогда, когда радиоволна сталкивается с любой неровной поверхностью или с поверхностью, размеры которой равны порядка или меньше, что приводит к распространению (рассеянию) или отражению энергии во всех направлениях. В городской местности обычные препятствия, вызывающие рассеивание сигнала, — это фонарные столбы, уличные знаки и листья. Название рассеивающий элемент (scatterer) применимо к любым препятствиям на пути распространения, которые являются причиной отражения или рассеяния сигнала.

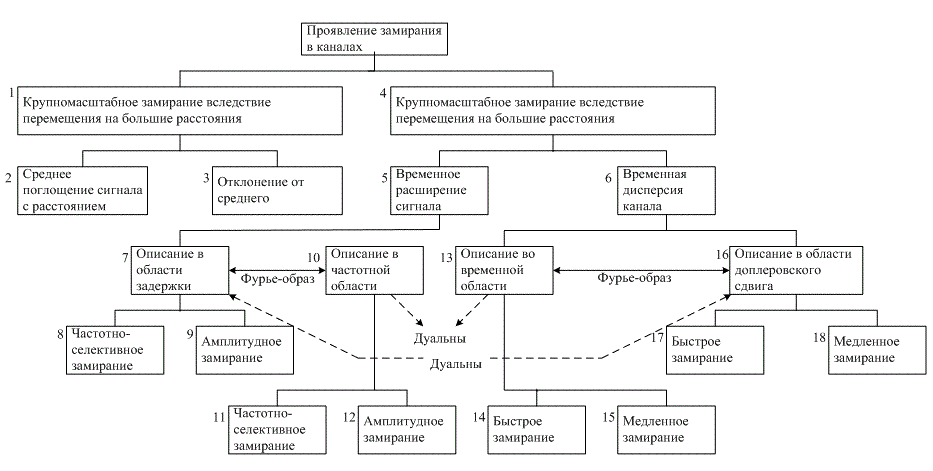
Рис. 15.1 Проявление замирания в канале

Рис. 15.1 можно использовать как оглавление следующих разделов. Два проявления мелкомасштабного замирания, временное расширение сигнала (дисперсия сигнала) и нестационарное поведение канала, будут исследованы в двух областях:, временной и частотной, как указано в блоках 7, 10, 13 и 16 (рис. 15.1). При дисперсии сигнала типы ухудшений характеристик, возникающих вследствие замирания, разделены на частотно-селективные или частотно-неселективные (амплитудные), как показано в блоках 8, 9, 11 и 12. При переменном во времени поведении типы ухудшений характеристик, возникающих вследствие замирания, разделены на быстрые и медленные, как показано в блоках 14, 15, 17 и 18. Пометки "Фурье-образы" и "дуальны" будут объяснены позже.

Удобной (но не совсем точной) иллюстрацией является рис. 15.2, показывающий различные вклады, которые должны рассматриваться при оценке потерь в тракте при анализе бюджета линии связи для мобильной радиосвязи [2]: (1) средние потери в тракте в результате крупномасштабного замирания как функция расстояния, (2) резерв крупномасштабного замирания в расчете на (почти) наихудший вариант отклонения от средних потерь в тракте (обычно 6-10 дБ) и (3) резерв релеевского или мелкомасштабного замирания в расчете на (почти) наихудший вариант (обычно 20-30 дБ). На рис. 15.2 примечание "= 1-2%" указывает предложенную область (вероятность) под хвостом каждой функции распределения вероятности, используемую как задачу разработки. Таким образом, величина указанного резерва предназначена для обеспечения достаточной мощности полученного сигнала для приблизительно 98-99% возможных значений замирания (крупно- и мелкомасштабного).

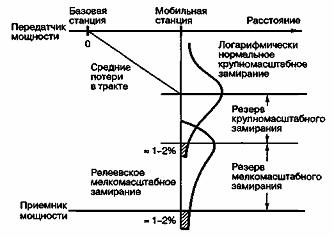
Рис. 15.2. Замирание в канале через бюджет линии связи.

(Источник: Greenwood D. and Hanto L. "Characterization: of Mobile Radio Channels". Mobile Radio Communications, edited by R. Steele,

Chapter 2, Pentech Press, London, 1994.)

С помощью комплексной формы записи переданный сигнал можно представить следующим образом.

s(t) = Re (15.2)

g(t) = (15.3)

где R(t) = |g(t)| — модуль огибающей, а — ее фаза. Для чистого фазово- или частотно-модулированного сигнала R(t) будет постоянным и в общем случае будет медленно изменяться по сравнению с t = 1/fc.

В среде с замиранием g(t) изменится на комплексный безразмерный множитель (его происхождение будет показано позже). Модифицированный узкополосный сигнал можно записать в виде . Рассмотрим амплитуду (t)R(t) этой огибающей, которую можно выразить через три положительных члена [3].

(t)R(t) = m(t)r0(t) R(t) (15.4)

Здесь m(t) называют компонентом крупномасштабного замирания огибающей, а r0(t) - компонентом мелкомасштабного замирания. Иногда m(t) именуют локальным средним, или логарифмически нормальным замиранием, поскольку его измеряемые значения можно статистически описать с помощью логарифмически нормальной функции распределения вероятностей; или, что равносильно, при измерении в децибелах m(t) имеет гауссову функцию распределения вероятностей. Кроме того, r0(t) иногда называют замиранием вследствие многолучевого распространения, или релеевским замиранием. На рис. 15.3 показана связь между (t) и m(t) для мобильной радиосвязи. В этом рисунке учтено, что была передана немодулированная несущая волна, а это в контексте уравнения (15.4) означает, что в любое время R(t) = 1. Типичный график зависимости мощности полученного сигнала от смещения антенны (обычно в единицах длины волны) показан на рис. 15.3, а. Мощность полученного сигнала является, конечно, функцией множителя (t). Можно без труда определить мелкомасштабные замирания, наложенные на крупномасштабные. Обычное изменение положения антенны, соответствующее переходу между соседними нулями изменения интенсивности сигнала вследствие мелкомасштабного замирания, равно приблизительно половине длины волны. На рис. 15.3, б крупномасштабное замирание или локальное среднее m(t) было удалено, чтобы показать мелкомасштабное замирание r0(t), относящееся к некоторой постоянной средней мощности. Напомним, что m(t) можно, как правило, оценить с помощью усреднения принятой огибающей по 10-30 длинам волн. Логарифмически нормально распределенное замирание является относительно медленно изменяющейся функцией местоположения. Следует отметить, что в приложениях, включающих движение, таких как использование радио в движущейся машине, зависимость от местоположения равносильна зависимости от времени. Ниже приведены некоторые подробности, касающиеся статистики и механизмов крупномасштабного и мелкомасштабного замираний.