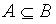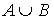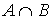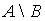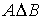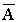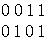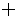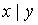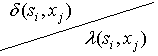1.1. Множества и отношения. Множества и элементы множеств
1.5. Табличный способ задания множеств
2.2. Логические связки (операции) над высказываниями
2.3. Пропозициональные формулы
2.4. Булевы функции. Таблицы истинности
2.5. Булевы функции одной переменной
2.6. Булевы функции двух переменных
2.7. Существенные и несущественные переменные
2.8. Равносильные формулы. Основные равносильности
2.11. Понятие двойственной функции
2.12. Некоторые двойственные функции
2.13. Элементарные канонические формы
2.15. Приведение формул к нормальным формам
2.17. Полные системы функций. Полином Жегалкина
3.1. Основные понятия и определения
3.2. Смежность, инцидентность, степени
3.4. Подграфы. Операции на графах
3.5. Связность. Компоненты связности. Маршруты и пути
3.6. Эйлеровы и гамильтоновы графы
3.8. Цикломатическое число графа. Построение остовного дерева связного графа
4.1. Понятие конечного детерминированного автомата
4.2. Способы задания автоматов
4.3. Эквивалентные состояния. Минимизация к.д.а
4.4. Алгоритм минимизации конечного автомата
4.5. Каноническая таблица. Канонические уравнения
4.6. Функциональные и логические элементы. Проектирование дискретных устройств
1. Теория множеств
1.1. Множества и отношения
Множества и элементы множеств
Определение. Множество – любая определенная совокупность объектов произвольной природы. Обозначают множества прописными латинскими буквами: A, B, ¼ , а его элементы обозначаются строчными латинскими буквами: a, b, ¼.
Например:
![]() (
(![]() является элементом множества
является элементом множества ![]() ("
("![]() принадлежит A")),
принадлежит A")),
![]() (
(![]() не является элементом множества A).
не является элементом множества A).
Определение. Пустое множество – это множество, не содержащее ни одного элемента, обозначается оно символом: Æ.
Определение. ![]() – универсальное множество (универсум) – множество, из которого берутся элементы в конкретном рассуждении.
– универсальное множество (универсум) – множество, из которого берутся элементы в конкретном рассуждении. ![]() – множество, рассматриваемое как наиболее общее в данной ситуации.
– множество, рассматриваемое как наиболее общее в данной ситуации.
Множество элементов ![]() , удовлетворяющих свойству P(x) обозначается
, удовлетворяющих свойству P(x) обозначается ![]() .
.
Примеры.
![]() – множество натуральных чисел;
– множество натуральных чисел;
![]() – множество вещественных чисел.
– множество вещественных чисел.
![]() – множество комплексных чисел.
– множество комплексных чисел.
1.2. Сравнение множеств
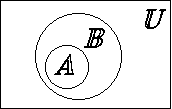
Определение. ![]() (А содержится в В или В включает А), если
(А содержится в В или В включает А), если ![]() . А называется подмножеством В. Если
. А называется подмножеством В. Если ![]() и
и 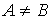 , то А называется строгим (собственным) подмножеством В. Обозначается это
, то А называется строгим (собственным) подмножеством В. Обозначается это ![]() .
.
Определение.  если они являются подмножествами друг друга, то есть
если они являются подмножествами друг друга, то есть ![]() или
или ![]()
Определение. Мощность конечного множества ![]() – число его элементов. Мощность бесконечного множества равна ¥.
– число его элементов. Мощность бесконечного множества равна ¥.
1.3. Операции над множествами
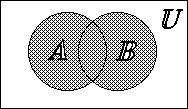
Определение. Объединением множеств А и В (![]() ) называется множество, состоящее из элементов, принадлежащих хотя бы одному из них.
) называется множество, состоящее из элементов, принадлежащих хотя бы одному из них. ![]()
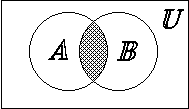
Определение. Пересечением множеств А и В (![]() ) называется множество, состоящее из элементов, принадлежащих и первому и второму одновременно.
) называется множество, состоящее из элементов, принадлежащих и первому и второму одновременно. ![]()
Определение. Разностью множеств А и В (![]() ) называется множество, состоящее из элементов множества А, не принадлежащих множеству В.
) называется множество, состоящее из элементов множества А, не принадлежащих множеству В. ![]()
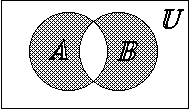
Определение. Симметрической разностью множеств А и В (![]() ) называется множество, состоящее из элементов множества А, не являющихся элементами множества В и элементов множества В, не являющихся элементами множества А.
) называется множество, состоящее из элементов множества А, не являющихся элементами множества В и элементов множества В, не являющихся элементами множества А. ![]()
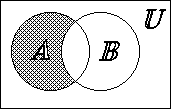
Определение. Дополнением множества А (![]() ) называется множество, состоящее из элементов множества U, не принадлежащих множеству А.
) называется множество, состоящее из элементов множества U, не принадлежащих множеству А.
![]()
Пример: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() зависит от того, какое U. Если
зависит от того, какое U. Если ![]() , то
, то ![]() , если
, если ![]() , то
, то ![]() .
.
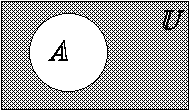
1.4. Диаграммы Эйлера-Венна
Диаграммы Эйлера-Венна – это геометрическое представление множеств. Множество U изображается прямоугольником, рассматриваемые множества – фигурами (окружностями). Для выделения результата применяется штриховка.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.5. Табличный способ задания множеств
Пусть задано множество U. Рассмотрим произвольное его подмножество ![]() и элемент
и элемент ![]() .
.
Определение. Индикаторной (характеристической) функцией для множества A называется функция
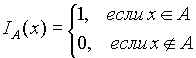 .
.
Таким образом: ![]() .
.
Для ![]() имеют место свойства:
имеют место свойства:
![]()
![]() ;
;
![]()
![]()
![]()
![]()
![]()
Индикаторы удобно задавать с помощью таблиц:
|
|
|
|
|
|
|
|
|
0 0 1 1 |
0 1 0 1 |
0 1 1 1 |
0 0 0 1 |
0 0 1 0 |
1 1 0 0 |
0 1 1 0 |
1.6. Свойства операций над множествами
Объединение и пересечение:
1. ![]() =
=![]() – коммутативность
– коммутативность
2. ![]() =
=![]() – коммутативность
– коммутативность
3. ![]() – ассоциативность
– ассоциативность
4. ![]() – ассоциативность
– ассоциативность
5. ![]() – дистрибутивность
– дистрибутивность
6. ![]() – дистрибутивность
– дистрибутивность
7. 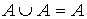 – идемпотентность
– идемпотентность
8. 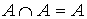 – идемпотентность
– идемпотентность
9. ![]() – свойство дополнения
– свойство дополнения
10. ![]() – свойство дополнения
– свойство дополнения
11. ![]() – закон де Моргана
– закон де Моргана
12. ![]() – закон де Моргана
– закон де Моргана
13. ![]() – свойство нуля
– свойство нуля
14. ![]() – свойство нуля
– свойство нуля
Дополнение:
15. ![]() – инволютивность
– инволютивность
16. ![]()
17. ![]()
Разность, симметрическая разность:
18. ![]()
19. ![]()
20. 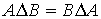
21. ![]()
22. ![]()
23. ![]()
1.7. Отношения
Определение. Пусть A и B произвольные множества. Декартовым произведением множеств A и B называется множество всевозможных упорядоченных пар, в которых первый элемент принадлежит множеству A, а второй – множеству B.
![]()
Пример.![]() – точки плоскости.
– точки плоскости.
Свойства декартовых произведений
1.![]()
2.![]()
3.![]()
4.![]()
5.![]()
6.![]()
Понятие отношения.
Отношение это один из способов задания взаимосвязей между элементами множества.
Унарные (одноместные) отношения отражают наличие какого-либо признака R у элемента множества A. Например, "быть четным" на множестве натуральных чисел. Все элементы множества A, отличающиеся признаком R , образуют подмножество множества A, называемое отношением R.
Бинарные отношения
Бинарные (двуместные) отношения используются для определения взаимосвязей, которыми характеризуются пары элементов множеств A и B. Все пары ![]() элементов множеств A и B, находящиеся в отношении R , образуют подмножество множества
элементов множеств A и B, находящиеся в отношении R , образуют подмножество множества ![]() .
.
Определение. Бинарное отношение – это тройка множеств ![]() , где
, где ![]() – график отношения. Пишут
– график отношения. Пишут ![]() или aRb.
или aRb.
Область определения : ![]() ;
;
Область значений: ![]() ;
;
Обратное отношение: ![]() ;
;
Композиция отношений ![]() и
и ![]() :
:
![]() .
.
Частичным порядком (пишут ![]() ), если оно рефлексивно, антисимметрично и транзитивно.
), если оно рефлексивно, антисимметрично и транзитивно.
1.8. Специальные бинарные отношения
Бинарное отношение ![]() на A называется
на A называется
- Рефлексивным, если
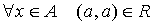 ;
; - Симметричным, если
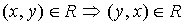 ;
; - Транзитивным, если
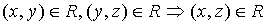 ;
; - Антисимметричным, если
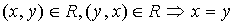 ;
; - Отношением эквивалентности на
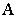 (пишут
(пишут 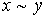 ), если оно рефлексивно, симметрично и транзитивно;
), если оно рефлексивно, симметрично и транзитивно;
Определение. Бинарное отношение ![]() называется функцией из
называется функцией из ![]() в
в ![]() , если
, если ![]() и
и ![]() .
.
Функция ![]() называется
называется
- Сюръективной, если
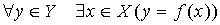 ;
; - инъективной, если
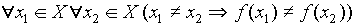 ;
; - биективной, если она сюръективна и инъективна.
2. Математическая логика
2.1. Высказывания
Определение. Высказывание – повествовательное утверждение, которое либо истинно либо ложно (не то и другое одновременно).
Примеры высказываний: "Тише едешь – дальше будешь", "Париж – столица Франции". Но "Как бы чего не вышло" или "Миру – мир" не являются высказываниями.
Определение. Высказывание называется простым (элементарным), если оно рассматривается как одно неделимое целое.
Определение. Сложное высказывание – высказывание, составленное из простых с помощью логических связок.
2.2. Логические связки (операции) над высказываниями
Определение. Конъюнкцией ("и") высказываний P и Q называется высказывание, истинное тогда и только тогда, когда оба истинны. Обозначается P&Q.
Таблица истинности:
|
P |
Q |
P&Q |
|
л |
л |
л |
|
л |
и |
л |
|
и |
л |
л |
|
и |
и |
и |
Определение. Дизъюнкцией ("или") высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба ложны. Обозначается ![]() .
.
Таблица истинности:
|
P |
Q |
|
|
л |
л |
л |
|
л |
и |
и |
|
и |
л |
и |
|
и |
и |
и |
Определение. Отрицанием ("не") высказывания P называется высказывание, ложное тогда и только тогда, когда P истинно. Обозначается ![]() или
или ![]() .
.
Таблица истинности:
|
P |
|
|
л |
и |
|
и |
л |
Определение. Импликацией высказываний P и Q называется высказывание, ложное, когда P истинно, а Q ложно, и истинное во всех остальных случаях. Обозначается 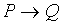 .
.
Таблица истинности:
|
P |
Q |
|
|
л |
л |
и |
|
л |
и |
и |
|
и |
л |
л |
|
и |
и |
и |
Определение. Эквивалентностью высказываний P и Q называется высказывание истинное, когда истинностные значения P и Q совпадают, и ложное в противном случае. Обозначается ![]() или
или ![]() .
.
Таблица истинности:
|
P |
Q |
|
|
л |
л |
и |
|
л |
и |
л |
|
и |
л |
л |
|
и |
и |
и |
Определение. Неравнозначностью (сложение по модулю 2) высказываний P и Q называется высказывание истинное, когда истинностные значения P и Q различны, и ложное в противном случае. Обозначается ![]() .
.
Таблица истинности:
|
P |
Q |
|
|
л |
л |
л |
|
л |
и |
и |
|
и |
л |
и |
|
и |
и |
л |
2.3. Пропозициональные формулы
Рассмотрим алфавит ![]() , где
, где ![]() ,
, ![]() ,
,![]() .
.
Символы из ![]() называются переменными высказывания или пропозициональными переменными.
называются переменными высказывания или пропозициональными переменными.
Символы из ![]() называются логическими связками.
называются логическими связками.
Скобки из ![]() называются вспомогательными символами.
называются вспомогательными символами.
Определение. Пропозициональная формула определяется следующим образом:
1) пропозициональная переменная есть формула;
2) если P и Q – формулы, то Ø P, (P&Q), (PÚ Q) ,(P® Q) ,(PÅ Q) ,(P|Q), (P¯ Q) – формулы,
3) других формул нет.
При этом
а) внешние скобки у формул опускаются;
б) устанавливаются следующие приоритеты:
Ø – выполняется в первую очередь;
& – во вторую очередь;
Ú , ® , Å , |, ¯ – в третью очередь.
2.4. Булевы функции. Таблицы истинности
Определение. Булевой функцией 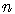 булевых переменных называется функция с областью определения
булевых переменных называется функция с областью определения 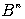 и областью значений
и областью значений ![]() , где
, где ![]() .
.
Способы задания:
1) таблицами истинности; при этом 0 интерпретируется как "ложь", а 1 – как "истина";
2) пропозициональными формулами.
Таблица истинностей некоторых логических связок:
|
x |
y |
x&y |
xÚ y |
Ø x |
x® y |
XÅ y |
x~y |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
2.5. Булевы функции одной переменной
|
|
|
Обозначение |
Наименование |
|
|
|
|
Константа 0 |
|
|
|
|
Тождественная |
|
|
|
|
Отрицание |
|
|
|
|
Константа 1 |
2.6. Булевы функции двух переменных
|
|
|
Обозначение |
Наименование |
|
|
0 0 0 0 |
|
Константа 0 |
|
|
0 0 0 1 |
|
Конъюнкция |
|
|
0 0 1 0 |
|
|
|
|
0 0 1 1 |
|
|
|
|
0 1 0 0 |
|
|
|
|
0 1 0 1 |
|
|
|
|
0 1 1 0 |
|
Сложение |
|
|
0 1 1 1 |
|
Дизъюнкция |
|
|
1 0 0 0 |
|
Стрелка Пирса |
|
|
1 0 0 1 |
|
Эквиваленция |
|
|
1 0 1 0 |
||
|
|
1 0 1 1 |
|
Импликация |
|
|
1 1 0 0 |
|
|
|
|
1 1 0 1 |
|
Импликация |
|
|
1 1 1 0 |
|
Штрих Шеффера |
|
|
1 1 1 1 |
1 |
Константа 1 |
2.7. Существенные и несущественные переменные
Определение. Переменная ![]() называется существенной для булевой функции
называется существенной для булевой функции ![]() , если
, если
![]()
![]() .
.
Определение. Переменная ![]() называется несущественной для булевой функции
называется несущественной для булевой функции ![]() , если
, если ![]()
![]() .
.
2.8. Равносильные формулы. Основные равносильности
Определение. Формула называется тождественно истинной, или тавтологией, если эта формула принимает значение 1 при всех наборах значений переменных.
Определение. Формула называется тождественно ложной, или противоречием, если эта формула принимает значение 0 при всех наборах значений переменных.
2.9. Основные тавтологии
|
1. |
Закон исключенного третьего |
|
2. |
|
|
3. |
|
|
4. |
Цепное рассуждение |
|
5. |
|
|
6. |
Определение. Формулы P и Q называются равносильными (обозначается ![]() ), если при любых значениях переменных значение формулы P совпадает со значением Q.
), если при любых значениях переменных значение формулы P совпадает со значением Q.
2.10. Основные равносильности
|
1. |
Коммутативность |
|
3. 4. |
Ассоциативность |
|
5. 6. |
Дистрибутивность |
|
7. |
Идемпотентность |
|
9. |
Законы исключенного третьего и противоречия |
|
11. 12. |
Законы де Моргана |
|
13. 14. |
Законы поглощения |
|
15. |
Правило склеивания |
|
16. 18. |
|
|
20. |
Закон двойного отрицания |
|
21. 22. 23. 24. |
|
|
25. |
Коммутативность |
|
26. |
Ассоциативность |
|
27. |
Дистрибутивность |
|
28. 30. |
Замечание. Здесь P, Q и R —пропозициональные формулы.
2.11. Понятие двойственной функции
Определение. Функцией, двойственной к булевой функции ![]() , называется функция
, называется функция ![]() .
.
Определение. Функция называется самодвойственной, если ![]() .
.
Теорема. (Принцип двойственности.) Пусть ![]() ,…,
,…,![]() и
и ![]() — булевы функции и пусть
— булевы функции и пусть ![]() =
=![]() - сложная булева функция. Тогда
- сложная булева функция. Тогда
![]() =
=![]()
Следствие. Пусть P и Q —формулы. Если ![]() , тогда
, тогда ![]() .
.
Принцип двойственности позволяет получать из доказанных равносильностей целый ряд новых. Кроме того, СКНФ(f)=![]() .
.
2.12. Некоторые двойственные функции
|
|
|
|
|
1. |
|
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
|
5. |
|
|
|
Замечание. |
||
2.13. Элементарные канонические формы
Определение. Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более 1 раза.
Определение. Элементарной дизъюнкцией называется дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более 1 раза.
2.14. Нормальные формы формул
Определение. Дизъюнктивной нормальной формой (Д.Н.Ф.) называется произвольная дизъюнкция элементарных конъюнкций.
Определение. Конъюнктивной нормальной формой (К.Н.Ф.) называется произвольная конъюнкция элементарных дизъюнкций.
Определение. К.Н.Ф. называется совершенной и обозначается С.К.Н.Ф., если каждая переменная входит в каждую элементарную дизъюнкцию ровно один раз с отрицанием или без.
Определение. Д.Н.Ф. называется совершенной и обозначается С.Д.Н.Ф, если каждая переменная входит в каждую элементарную конъюнкцию ровно один раз с отрицанием или без.
Пример:![]() – Д.Н.Ф;
– Д.Н.Ф; ![]() – С.Д.Н.Ф.
– С.Д.Н.Ф.
Теорема. Любая логическая функция кроме 0 имеет единственную С.Д.Н.Ф: ![]() .
.
Теорема. Любая логическая функция кроме 1 имеет единственную С.К.Н.Ф: ![]() .
.
Здесь 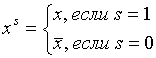 .
.
Пример. Пусть функция трех переменных задана таблицей истинности:
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Записать ее С.Д.Н.Ф. и С.К.Н.Ф.
С.Д.Н.Ф.(f)=![]()
С.К.Н.Ф.(f)=![]()
2.15. Приведение формул к нормальным формам
Любую логическую формулу (кроме 0) можно привести к С.Д.Н.Ф. следующим образом:
- Все не булевские операции заменить на булевские (&, Ú , Ø ) c помощью равносильностей:
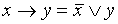 ;
; 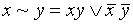 ;
; 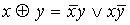 ;
; 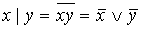 ;
; 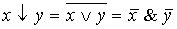 .
. - Все отрицания "спустить" до переменных с помощью законов де Моргана.
- Раскрыть скобки (дистрибутивность, ассоциативность).
- Удалить лишние конъюнкции, повторения переменных в конъюнкциях и константы.
Для приведения к С.Д.Н.Ф:
- Расщепить те конъюнкции, которые содержат не все переменные.
2.16. Минимизация д.н.ф.
Д.Н.Ф, содержащую минимальное число вхождений переменных, будем считать минимальной.
Приведем 2 наиболее простых метода минимизации Д.Н.Ф. функции:
- Группировка: элементарные конъюнкции
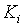 ,
, 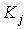 в ДНФ группируются в пары так, что после вынесения за скобку общего множителя K подформула
в ДНФ группируются в пары так, что после вынесения за скобку общего множителя K подформула 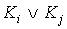 имела вид
имела вид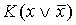 или
или 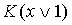 . Далее заменяем
. Далее заменяем 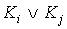 на эквивалентную ей конъюнкцию K.
на эквивалентную ей конъюнкцию K.
Пример:
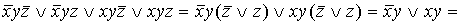
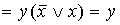 .
. - Метод Блейка состоит в применении двух правил:
а) обобщенное склеивание – первое правило. С помощью формулы ![]() производим операцию обобщенного склеивания в Д.Н.Ф. пока это возможно. Для этого в Д.Н.Ф. отыскиваем подформулы вида
производим операцию обобщенного склеивания в Д.Н.Ф. пока это возможно. Для этого в Д.Н.Ф. отыскиваем подформулы вида ![]() и добавляем к ним
и добавляем к ним ![]() . На этом этапе формула усложняется.
. На этом этапе формула усложняется.
б) поглощение – второе правило. Оно основано на равенстве
![]() .
.
Находим в Д.Н.Ф. конъюнкции с минимальным числом сомножителей и все конъюнкции, их содержащие, вычеркиваем.
Пример: ![]() .
.
Разумно в Д.Н.Ф. сначала применить метод группировки (как более простой), а затем метод Блейка.
2.17. Полные системы функций. Полином Жегалкина
Определение. Множество булевых функций называется полной системой, если любая булева функция может быть выражена через функции этого множества с помощью суперпозиции. Минимальная полная система называется базисом.
Примеры базисов:
![]() — дизъюнктивный базис;
— дизъюнктивный базис;
![]() — конъюнктивный базис;
— конъюнктивный базис;
![]() — базис Жегалкина;
— базис Жегалкина;
![]() — базис Пирса;
— базис Пирса;
![]() — базис Шеффера.
— базис Шеффера.
Определение Логическая функция, представленная над базисом ![]() называется многочленом Жегалкина. Он имеет вид:
называется многочленом Жегалкина. Он имеет вид:
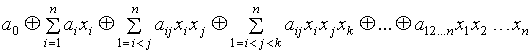 ,
,
где константы ![]() .
.
2.18. Функционально замкнутые классы функций
Ведем следующие классы Поста:
![]() =
=![]() – Класс функций, сохраняющих 0.
– Класс функций, сохраняющих 0.
![]() =
=![]() – Класс функций, сохраняющих 1.
– Класс функций, сохраняющих 1.
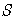 =
=![]() – Класс самодвойственных функций.
– Класс самодвойственных функций.
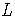 =
=![]() – Класс линейных функций.
– Класс линейных функций.
![]() =
=![]() – Класс монотонных функций.
– Класс монотонных функций.
Каждый класс Поста является функционально замкнутым, т.е. все функции, реализованные формулами над данным классом, также принадлежат данному классу.
Таблица принадлежности функциональным классам основных булевых функций:
|
|
|
|
|
|
|
|
|
- |
- |
|
|
- |
|
|
|
|
- |
- |
|
|
|
|
|
- |
- |
|
|
|
- |
|
- |
- |
- |
|
|
|
- |
- |
|
- |
|
|
- |
|
- |
|
- |
|
|
- |
- |
- |
- |
- |
Теорема. (Теорема Поста.) Для того, чтобы система булевых функций ![]() была полной, необходимо и достаточно, чтобы для каждого из классов
была полной, необходимо и достаточно, чтобы для каждого из классов ![]() ,
, ![]() ,
, 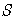 ,
, 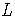 ,
, ![]() нашлась функция
нашлась функция ![]() из системы, не принадлежащая данному классу.
из системы, не принадлежащая данному классу.
2.19. Понятие алгоритма. Описание машины Тьюринга
Для решения ряда однотипных задач иногда целесообразно использовать чисто механические вычислительные процессы. Описание таких процессов называют алгоритмами.
Интуитивно: алгоритм – это некоторое формальное предписание, действуя согласно которому, можно получить решение задачи. Примеры алгоритмов:
- Нахождение наибольшего общего делителя двух натуральных чисел.
- Извлечение корня квадратного из рационального числа с заданной точностью.
- Вычисление ранга матрицы, и так далее.
Перечисленные алгоритмы имеют ряд общих черт, которые естественно считать присущими любому алгоритму:
Дискретность. Решение задачи разбивается на этапы, каждый из которых прост и локален.
Детерминированность. После выполнения очередного этапа однозначно определено, что сделать на следующем этапе.
Направленность. Должно быть указано, что считать результатом применения алгоритма.
Массовость. Алгоритм служит для решения целого класса однотипных задач.
Конечность. Для решения задачи выполняется конечная последовательность шагов алгоритма.
Тезис Тьюринга Всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга.
Определение. Машиной Тьюринга (м-т) называется тройка ![]() , где
, где ![]() —внешний алфавит, обычно
—внешний алфавит, обычно ![]() ;
; ![]() —внутренний алфавит, элементами которого являются состояния управляющего устройства,
—внутренний алфавит, элементами которого являются состояния управляющего устройства, ![]() —заключительное состояние,
—заключительное состояние, ![]() —начальное состояние;
—начальное состояние; ![]() —программа, состоящая из команд вида:
—программа, состоящая из команд вида: ![]() , где
, где ![]() —один из символов:
—один из символов: ![]() (налево),
(налево), ![]() (направо),
(направо), ![]() (на месте),
(на месте), ![]() ,
, ![]() .
.
Имеется бесконечная в обе стороны лента, разбитая на ячейки. В начальный момент в конечном числе ячеек записаны символы из ![]() , в остальных ячейках записан пустой символ, обозначаемый через
, в остальных ячейках записан пустой символ, обозначаемый через ![]() . Машина Тьюринга имеет головку, которая в любой момент времени обозревает некоторую ячейку, и управляющее устройство, которое может находиться в одном из состояний
. Машина Тьюринга имеет головку, которая в любой момент времени обозревает некоторую ячейку, и управляющее устройство, которое может находиться в одном из состояний ![]() .
.
Шаг работы м-т. Если м-т имеет состояние ![]() , в обозреваемой ячейке записан символ
, в обозреваемой ячейке записан символ ![]() , то выполняется команда
, то выполняется команда ![]() , м-т переходит в состояние
, м-т переходит в состояние ![]() , в ячейке на место
, в ячейке на место ![]() , записывается
, записывается ![]() и головка сдвигается влево, вправо или остается на месте в зависимости от символа
и головка сдвигается влево, вправо или остается на месте в зависимости от символа ![]() .
.
В начальный момент м-т находится в состоянии ![]() , останавливается м-т, если перейдет в одно из заключительных состояний либо при отсутствии команды, которую можно выполнить.
, останавливается м-т, если перейдет в одно из заключительных состояний либо при отсутствии команды, которую можно выполнить.
Конфигурацией (машинным словом) называется слово ![]() , где
, где ![]() — слово на ленте левее головки,
— слово на ленте левее головки, ![]() — слово правее головки, включая символ под головкой.
— слово правее головки, включая символ под головкой.
Говорят, что м-т ![]() применима к слову
применима к слову ![]() , если
, если ![]() , начав работу на слове
, начав работу на слове ![]() , машина остановится через конечное число шагов; если в результате получится слово
, машина остановится через конечное число шагов; если в результате получится слово ![]() , то пишут
, то пишут ![]() . Если
. Если ![]() не остановится, то она не применима к слову
не остановится, то она не применима к слову ![]() .
.
3. Теория графов
3.1. Основные понятия и определения
Граф (от греческого ![]() - пишу) - непустое множество вершин
- пишу) - непустое множество вершин ![]() и набор
и набор ![]() неупорядоченных и упорядоченных пар вершин вида (v,w). Обычно граф обозначают как G(V,E); количество вершин и ребер обозначается, соответственно, n(G) и m(G).
неупорядоченных и упорядоченных пар вершин вида (v,w). Обычно граф обозначают как G(V,E); количество вершин и ребер обозначается, соответственно, n(G) и m(G).
Неупорядоченная пара вершин называется ребром {v,w}, упорядоченная пара - дугой (v,w).
Граф, содержащий только ребра, называется неориентированным (обозначается G). Граф, содержащий только дуги - ориентированным (или орграфом) (обозначается ![]() ).
).
Пара вершин может быть соединена двумя или более рёбрами (или, соответственно, дугами одного направления), такие рёбра (или дуги) называются кратными. Дуга (или ребро) может начинаться и заканчиваться в одной и той же вершине, в этом случае соответствующая дуга (или ребро) называется петлёй.
Граф без кратных рёбер и петель называется простым графом.
Граф, все n вершин которого являются изолированными, называется нулевым (пустым) и обозначается ![]() .
.
Простой граф, любые две вершины которого являются смежными, называется полным. Полный граф с n вершинами обозначается ![]() .
.
3.2. Смежность, инцидентность, степени
Вершины, соединённые ребром или дугой, называются смежными.
Рёбра, имеющие общую вершину, тоже называются смежными.
Ребро (или дуга) и любая из его вершин называются инцидентными.
Говорят, что ребро {v,w} соединяет вершины v и w. Для орграфов: дуга (v,w) начинается в вершине v (исходит из вершины v) и заканчивается в вершине w (заходит в вершину w), или идет из вершины v в вершину w.
Степенью вершины v графа G называется число deg v рёбер графа G, инцидентных вершине v, при этом петли учитываются дважды. Вершина графа, имеющая степень 0, называется изолированной, а степень 1 - тупиковой (висячей, концевой).
Для орграфа: полустепенью исхода (захода) вершины v орграфа ![]() называется число
называется число ![]() (
(![]() ) дуг орграфа, исходящих из вершины v (заходящих в вершину v), при этом каждая петля, инцидентная вершине v , учитывается как в
) дуг орграфа, исходящих из вершины v (заходящих в вершину v), при этом каждая петля, инцидентная вершине v , учитывается как в ![]() , так и в
, так и в ![]() .
.
Теорема. (Теорема о рукопожатиях) Сумма степеней всех вершин графа G равна удвоенному числу его рёбер, то есть: ![]() . (Число пожатых рук всегда четно.)
. (Число пожатых рук всегда четно.)
Для орграфа: ![]() .
.
Доказательство следует из тех соображений, что каждое ребро вносит в сумму вклад 2.
Следствие. В каждом графе число вершин нечётной степени чётно.
3.3. Способы задания графов
- Рисунок.
- Список вершин и рёбер.
- Матрица смежности. Матрицей смежности называется квадратная матрица A(G)=(
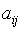 ), (i,j=1,…,n), у которой элемент
), (i,j=1,…,n), у которой элемент 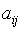 равен числу рёбер, соединяющих
равен числу рёбер, соединяющих 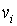 и
и 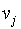
Для орграфа элемент матрицы A(
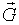 ),
), 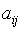 равен числу дуг, идущих из
равен числу дуг, идущих из 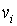 в
в 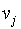 .
. - Матрица инцидентности. Матрицей инцидентности графа G (без петель) называется матрица B(G)=(
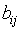 ) (для орграфа B(
) (для орграфа B(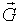 )=(
)=(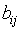 )) размерности
)) размерности 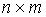 , у которой:
, у которой:
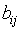 =1, если вершина
=1, если вершина 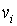 инцидентна ребру
инцидентна ребру  ,
,
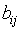 =0, в противном случае.
=0, в противном случае.
Для орграфа:
![]() =1, если вершина
=1, если вершина ![]() есть начало дуги
есть начало дуги ![]() ;
;
![]() = - 1, если вершина
= - 1, если вершина ![]() есть конец дуги
есть конец дуги ![]() ;
;
![]() =0, если
=0, если ![]() и
и ![]() не инцидентны.
не инцидентны.
Примеры:
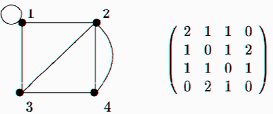
Граф и его матрица смежности.
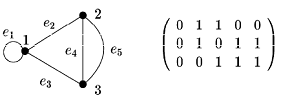
Граф и его матрица инцидентности, здесь вершинам соответствуют строки, а ребрам - столбцы.
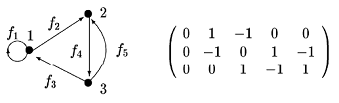
Матрица инцидентности для ориентированного графа, здесь вершинам соответствуют строки, а дугам - столбцы.
3.4. Подграфы. Операции на графах
Подграфом графа G(V,E) называется граф, все вершины и ребра которого содержатся среди вершин и ребер исходного графа G(V,E).
Определим некоторые операции на графах.
Удаление или добавление ребра.
Удаление вершины. Из множества вершин удаляем выбранную вершину, а из множества ребер все инцидентные ей ребра.
Стягивание ребра. Отождествляем (стягиваем) вершины инцидентные выбранному ребру.
Добавление вершины (разбиение ребра). Выберем некоторое ребро (u,v) из множества ребер и удалим его. В множество вершин добавим новую вершину w, а в множество ребер новые ребра (u,w) и (w,v).
Объединение графов. Объединением графов ![]() и
и ![]() называется граф
называется граф ![]() .
.
Пересечение графов. Пересечением графов ![]() и
и ![]() (
(![]() ) называется граф
) называется граф ![]() .
.
3.5. Связность. Компоненты связности. Маршруты и пути
Маршрут в графе - это последовательность вершин и рёбер ![]() , где любые два "соседа" инцидентны. Рёбра и вершины в маршруте могут повторяться. Если начальная и конечная вершины совпадают, то маршрут называется замкнутым. Если все вершины и рёбра маршрута различны, то он называется цепью. Замкнутая цепь - это цикл. Длина маршрута равна числу входящих в него рёбер.
, где любые два "соседа" инцидентны. Рёбра и вершины в маршруте могут повторяться. Если начальная и конечная вершины совпадают, то маршрут называется замкнутым. Если все вершины и рёбра маршрута различны, то он называется цепью. Замкнутая цепь - это цикл. Длина маршрута равна числу входящих в него рёбер.
Граф G(V,E) называется связным, если для любых его вершин существует соединяющий их маршрут. Компонентой связности называется максимальный связный подграф графа G(V,E). Число компонент связности графа обозначается k(G).
Ориентированный граф G(V,![]() ) называется сильно связным, если для любых его вершин u и v существуем путь из u в v и путь из v в u.
) называется сильно связным, если для любых его вершин u и v существуем путь из u в v и путь из v в u.
В этом случае говорят, что вершины u и v достижимы друг из друга.
Если для любых двух вершин u и v графа G(V,![]() ) существует маршрут из u в v или из v в u, то граф называется связным или односторонне связным.
) существует маршрут из u в v или из v в u, то граф называется связным или односторонне связным.
Вершина, удаление которой увеличивает число компонент связности, называется точкой сочленения. Ребро, удаление которого увеличивает число компонент связности, называется перешейком (мостом).
3.6. Эйлеровы и гамильтоновы графы
Цикл в графе называется эйлеровым, если он проходит через каждое ребро графа ровно один раз. Граф называется эйлеровым, если в нем есть эйлеров цикл.
Теорема. Граф является эйлеровым тогда и только тогда, когда граф связный и все вершины имеют четную степень.
Теорема. Ориентированный граф является эйлеровым тогда и только тогда, когда он сильно связный и для любой его вершины имеет место равенство: ![]() =
=![]() .
.
Свое название эйлеровы графы получили в честь Л.Эйлера, который первым рассмотрел такие графы в 1736 году в своей знаменитой работе о кенигсбергских мостах. Этой работой Эйлер, по существу, положил начало новому разделу математики - теории графов.
Задача о кенигсбергских мостах состояла в следующем. На реке Прегель в Кенигсберге было два острова, соединенных между собой и с берегами семью мостами, как показано на рисунке:
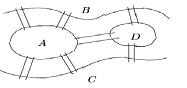
Спрашивается, можно ли, начиная с некоторого места суши, обойти все мосты ровно по одному разу и вернуться в начальную точку? Эйлер предложил рассмотреть следующий граф:
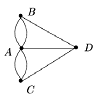
Нетрудно догадаться, что решение этой задачи сводится к поиску эйлеровой цепи в данном графе. Однако, как показывает приведенная теорема, в указанном графе нет эйлеровых цепей.
Цикл в графе называется гамильтоновым, если он проходит через каждую вершину графа ровно один раз. Граф называется гамильтоновым, если в нем есть гамильтонов цикл.
Указанные названия циклов связаны с именем Уильяма Гамильтона, который в 1859 году предложил следующую игру головоломку:
Требуется, переходя по очереди от одной вершины додекаэдра к другой вершине по его ребру, обойти все 20 вершин по одному разу и вернуться в начальную вершину.
Отметим, что придумано еще много других развлекательных и полезных задач, связанных с поиском гамильтоновых циклов. Сформулируем две из них:
1. Кампанию из нескольких человек требуется рассадить за круглым столом таким образом, чтобы по обе стороны от каждого сидели его знакомые.
Очевидно, для решения этой задачи нужно найти гамильтонов цикл в графе знакомств компании.
2. (Задача о шахматном коне.) Можно ли, начиная с произвольного поля шахматной доски, обойти конем последовательно все 64 поля по одному разу и вернуться в исходное поле?
Несмотря на внешнее сходство задач об эйлеровых и гамильтоновых циклах, оказалось, что эффективных критериев существования гамильтоновых циклов ( в отличии от эйлеровых) не существует.
3.7. Деревья и леса
Связный граф без циклов называется деревом.
Граф без циклов называется лесом.
Теорема. T(V,E) - дерево тогда и только тогда, когда T(V,E) - связный граф и |E|=|V| - 1.
Теорема. В любом дереве имеется не менее двух висячих вершин.
3.8. Цикломатическое число графа. Построение остовного дерева связного графа.
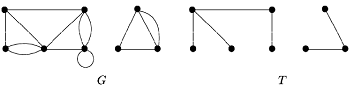
Остовным деревом связного графа G(V,E) называется любой его подграф, содержащий все вершины G и являющийся деревом.
На рисунке приведены два графа G и по одному из их остовных деревьев T.
Число ребер, которое необходимо удалить для получения остова, называется цикломатическим числом графа G и обозначается ![]() .
.
Теорема. Цикломатическое числом графа G(V,E) не зависит от последовательности удаления ребер и имеет место формула:
![]() = |E|| - |V|+k(G),
= |E|| - |V|+k(G),
где k(G) - число компонент связности.
4. Конечные детерминированные автоматы
4.1. Понятие конечного детерминированного автомата
Автоматы можно рассматривать как механизмы, состоящие из:
- блока управления, который может пребывать в различных состояниях (S внутренний алфавит);
- входного канала;
- выходного канала.
Входной канал считывает входные сигналы (Х) из внешней среды. Выходной канал выдает выходные сигналы (Y) во внешнюю среду. Работа автомата протекает в дискретные такты времени t=1,2,3,…. По команде ![]() в некотором такте времени
в некотором такте времени ![]() блок управления установлен в состоянии
блок управления установлен в состоянии ![]() и входной канал воспринимает
и входной канал воспринимает ![]() , тогда в этом же такте
, тогда в этом же такте ![]() в выходной канал выдается символ
в выходной канал выдается символ ![]() , а к следующему такту
, а к следующему такту ![]() +1 блок управления перейдет в состояние
+1 блок управления перейдет в состояние ![]() .
.
Определение. К.Д.А. называется система ![]() , где
, где ![]() - алфавит состояний,
- алфавит состояний, ![]() – входной алфавит,
– входной алфавит, ![]() – выходной алфавит. Множества S, X, Y – конечные.
– выходной алфавит. Множества S, X, Y – конечные.
![]() – функция переходов,
– функция переходов,
![]() – функция выходов.
– функция выходов.
Если в автомате выделено одно состояние , называемое начальным (обычно ![]() ), то автомат называется инициальным.
), то автомат называется инициальным.
4.2. Способы задания автоматов
-
- Таблица переходов–выходов.
|
S\X |
|
… |
|
… |
|
|
|
|||||
|
M |
|||||
|
|
|
||||
|
M |
|||||
|
|
-
- С помощью орграфов. Вершины граф означают состояния, а дуги – переходы между ними. Из каждой вершина исходит k дуг. Из вершины
 проводится дуга в вершину
проводится дуга в вершину 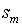 в том и только в том случае, когда
в том и только в том случае, когда 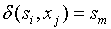 для некоторого
для некоторого 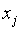 .
.
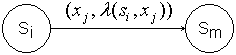
Этой дуге приписывается пометка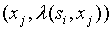 :
:
- С помощью орграфов. Вершины граф означают состояния, а дуги – переходы между ними. Из каждой вершина исходит k дуг. Из вершины
Начальное состояние в инициальном автомате помечается символом ![]() . Описанный таким образом орграф с пометками называется диаграммой Мура.
. Описанный таким образом орграф с пометками называется диаграммой Мура.
- С помощью канонических уравнений:
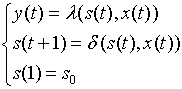
в момент t=1 автомат находится в начальном состоянии
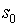 . В каждый момент t=1,2,3,… дискретного времени автомат, находясь в некотором состоянии s(t) из множества S, под действием входного сигнала
. В каждый момент t=1,2,3,… дискретного времени автомат, находясь в некотором состоянии s(t) из множества S, под действием входного сигнала 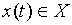 выдает выходной сигнал
выдает выходной сигнал 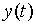 из множества Y, согласно функции выходов l , а затем меняет свое состояние на s(t+1) согласно функции переходов d.
из множества Y, согласно функции выходов l , а затем меняет свое состояние на s(t+1) согласно функции переходов d.
Для определения множества состояний автомата необходимо уяснить содержательный смысл и назначение понятия состояния.
После преобразования входного сигнала ![]() в выходной
в выходной ![]() его значение к следующему такту времени теряется. Иначе говоря, в любой тактовый момент t в устройстве нет информации о сигналах в предыдущие моменты, то есть о значениях
его значение к следующему такту времени теряется. Иначе говоря, в любой тактовый момент t в устройстве нет информации о сигналах в предыдущие моменты, то есть о значениях ![]() ,
,![]() ,
, ![]() ,… . Поэтому, если при вычислении значения функции переходов и выходов по формуле необходима информация об этих тактовых моментах, то ее нужно каким-либо образом "запомнить". В этом и состоит содержательное назначение состояний. Состояния – это вспомогательные объекты, которые подбираются таким образом, чтобы в совокупности с входным значением
,… . Поэтому, если при вычислении значения функции переходов и выходов по формуле необходима информация об этих тактовых моментах, то ее нужно каким-либо образом "запомнить". В этом и состоит содержательное назначение состояний. Состояния – это вспомогательные объекты, которые подбираются таким образом, чтобы в совокупности с входным значением ![]() однозначно определить выходное значение
однозначно определить выходное значение ![]() . Обычно состояния кодируют ту информацию, которая поступила до момента t.
. Обычно состояния кодируют ту информацию, которая поступила до момента t.
Пример. Построить таблицу переходов–выходов К.Д.А, реализующего функцию:
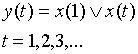
![]()
Чтобы на любом, отличном от первого, такте иметь информацию о ![]() , введем два следующих состояния:
, введем два следующих состояния:
![]() ={"на первом такте поступил 0"};
={"на первом такте поступил 0"};
![]() ={"на первом такте поступила 1"}.
={"на первом такте поступила 1"}.
И ![]() –начальное состояние.
–начальное состояние.
Построим таблицу переходов–выходов:
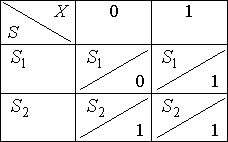
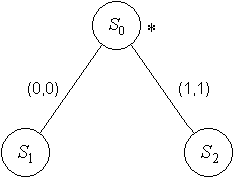
Для ![]() нарисуем диаграмму Мура:
нарисуем диаграмму Мура:
И дополним таблицу переходов–выходов:
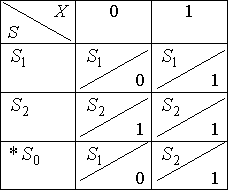
4.3. Эквивалентные состояния. Минимизация к.д.а
Определение. Две диаграммы Мура называются изоморфными, если они могут быть превращены одна в другую переобозначением вершин.
Определение. Два автомата называются изоморфными, если их диаграммы Мура изоморфны.
Рассмотрим два автомата ![]() и
и ![]() с одинаковыми входным и выходным алфавитами.
с одинаковыми входным и выходным алфавитами.
Определение. Состояния ![]() и
и ![]() называются неотличимыми (эквивалентными) тогда и только тогда, когда для любого входного слова х результат работы автомата
называются неотличимыми (эквивалентными) тогда и только тогда, когда для любого входного слова х результат работы автомата ![]() такой же, как и для
такой же, как и для ![]() .
.
![]()
В частном случае, когда ![]() =
=![]() , то речь идет о неотличимых состояниях одного автомата.
, то речь идет о неотличимых состояниях одного автомата.
Определение. Автоматы ![]() и
и ![]() называются неотличимыми (эквивалентными) тогда и только тогда, когда для любого состояния
называются неотличимыми (эквивалентными) тогда и только тогда, когда для любого состояния ![]() найдется эквивалентное ему состояние
найдется эквивалентное ему состояние ![]() и обратно.
и обратно.
Неотличимые автоматы осуществляют одно и то же отображение входных слов в выходные.
Определение. Автомат А называется приведенным, если в нем нет эквивалентных (неразличимых) состояний.
Число состояний в приведенном автомате минимально. Для любого автомата ![]() существует эквивалентный ему приведенный автомат А. Процедура нахождения такого автомата называется минимизацией автомата
существует эквивалентный ему приведенный автомат А. Процедура нахождения такого автомата называется минимизацией автомата ![]() .
.
4.4. Алгоритм минимизации конечного автомата
Шаг 1: два состояния s и t относим в один класс ![]() , если для любого входного символа x значение функции выхода s совпадает со значениями функции выхода t. В результате получим r классов:
, если для любого входного символа x значение функции выхода s совпадает со значениями функции выхода t. В результате получим r классов:
![]() .
.
M
Шаг k: два состояния s и t из одного класса ![]() , полученного на предыдущем шаге, относим в один класс
, полученного на предыдущем шаге, относим в один класс ![]() , если для любого значения входного символа значения функций состояний принадлежат одному и тому же классу из предыдущего шага. Если шаг k не изменяет разбиения, то процесс останавливается. Доопределяем функции перехода и выхода и строим таблицу переходов –выходов.
, если для любого значения входного символа значения функций состояний принадлежат одному и тому же классу из предыдущего шага. Если шаг k не изменяет разбиения, то процесс останавливается. Доопределяем функции перехода и выхода и строим таблицу переходов –выходов.
Пример. Минимизировать автомат, заданный таблицей:
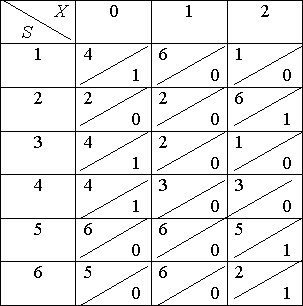
Шаг 1: Первое, третье и четвертое состояния отнесем в один класс состояний, а второе, пятое и шестое – в другой:
![]() ;
; ![]()
Шаг 2: Выпишем значения функции переходов для состояний из класса ![]() :
:
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
Видно, что 1 и 3-е состояния относим в один класс этого шага ![]() , а четвертое состояние – в другой
, а четвертое состояние – в другой ![]() . Проанализировав аналогичным образом значения функции выходов для состояний из класса
. Проанализировав аналогичным образом значения функции выходов для состояний из класса ![]() , видим:
, видим:
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]() , т.е. все они остаются в одном классе. В результате получим разбиение на классы:
, т.е. все они остаются в одном классе. В результате получим разбиение на классы:
![]() ;
; ![]() ;
; ![]()
Шаг 3: ![]() ;
; ![]() ;
; ![]() . Дальнейшего разбиения классов не происходит, поэтому процесс останавливается. Класс
. Дальнейшего разбиения классов не происходит, поэтому процесс останавливается. Класс ![]() назовем состоянием
назовем состоянием ![]() , класс состояний
, класс состояний ![]() назовем состоянием
назовем состоянием ![]() , а класс
, а класс ![]() – состоянием
– состоянием ![]() .
.
Построим таблицу переходов–выходов:
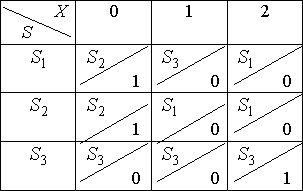
Построенный автомат – минимальный.
4.5. Каноническая таблица. Канонические уравнения
Реализация К.Д.А. осуществляется на основе канонических уравнений, которые находятся с помощью канонической таблицы. Каноническая таблица строится следующим образом по таблице переходов–выходов или диаграмме Мура.
Аргументы функций l и d находятся в столбцах слева, а справа – их значения.
|
S\X |
|
… |
|
… |
|
|
|
|||||
|
|
|||||
|
M |
|||||
|
|
|||||
|
M |
|||||
|
|
|
s(t) |
x(t) |
y(t) |
s(t+1) |
|
|
|
|
|
|
… |
… |
… |
… |
|
|
|
|
|
|
|
|
|
|
|
… |
… |
… |
… |
|
|
|
|
|
|
… |
… |
… |
… |
|
|
|
|
|
|
… |
… |
… |
… |
|
|
|
|
|
Канонические уравнения имеют вид:
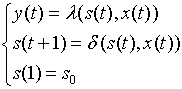
Элементы множеств S, X, Y кодируют двоичными наборами, соблюдая при этом следующие условия:
- разным элементам в каждом из множеств S, X, Y соответствуют разные кодовые наборы;
- длины кодовых наборов в каждом из множеств S, X, Y должны совпадать и быть по возможности минимальными;
- начальному состоянию соответствует набор
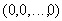 .
.
После кодирования ![]() ,
, ![]() ,
, ![]() принимают вид:
принимают вид:
![]() =
=![]()
![]() =
=![]()
![]() =
=![]()
Таблица преобразовывается к скалярному виду следующим образом:
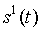 |
… | 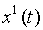 |
… | 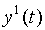 |
… | 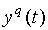 |
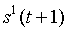 |
… | 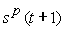 |
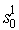 |
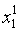 |
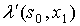 |
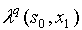 |
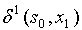 |
 |
||||
| … | . | … | … | … | … | … |
Для того, чтобы представить ![]() ,
, ![]() как булевы функции, необходимо, чтобы они были всюду определены. С этой целью к таблице добавляются строки, содержащие в левой части недостающие наборы, а в правой части – прочерки. Затем, прочерки заполняются 0 и 1 (функции доопределяются) так, чтобы по соответствующим столбцам значений l и d можно было записать формулу в виде СКНФ или СДНФ или в каком-нибудь другом наиболее простом виде.
как булевы функции, необходимо, чтобы они были всюду определены. С этой целью к таблице добавляются строки, содержащие в левой части недостающие наборы, а в правой части – прочерки. Затем, прочерки заполняются 0 и 1 (функции доопределяются) так, чтобы по соответствующим столбцам значений l и d можно было записать формулу в виде СКНФ или СДНФ или в каком-нибудь другом наиболее простом виде.
Пример. Автомат задан таблицей переходов – выходов:
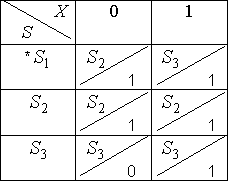
Записать его канонические уравнения.
Закодируем состояние ![]() 00 (начальное), состояние
00 (начальное), состояние ![]() 01, состояние
01, состояние ![]() 10.
10.
Запишем каноническую таблицу:
|
s(t) |
x(t) |
y(t) |
s(t+1) |
|
00 |
0 |
1 |
01 |
|
00 |
1 |
1 |
10 |
|
01 |
0 |
1 |
01 |
|
01 |
1 |
1 |
01 |
|
10 |
0 |
0 |
10 |
|
10 |
1 |
1 |
10 |
И преобразуем ее к скалярному виду:
|
|
|
x(t) |
y(t) |
|
|
|
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
Две последние строки доопределим следующим образом:
|
|
|
x(t) |
y(t) |
|
|
|
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
Запишем канонические уравнения:
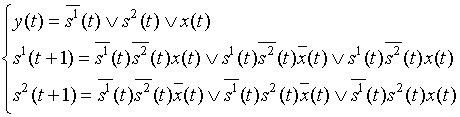 .
.
Осталось упростить уравнения.
Применим метод группировки
![]()
![]()
=![]() ;
;
![]()
![]()
=![]() ;
;
и запишем канонические уравнения в более простом виде:
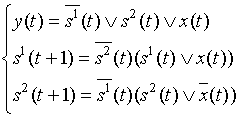
4.6. Функциональные и логические элементы. Проектирование дискретных устройств
Под функциональным элементом понимают устройство, реализующее элементарную функцию. Функциональные элементы, соответствующие булевым функциям, называют логическими элементами.
Канал – это линия, по которой передается информация. Узел – точка, в которую передается или из которой считывается информация. На схемах канал обозначается прямой линией, а узел – кружочком. Точки ветвления каналов обозначаются жирной точкой, чтобы отличать их от точек пересечения линий на схеме.
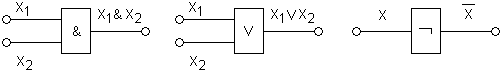
Построение схемы, реализующей булеву функцию.
1 ЭТАП: Функции l и d реализуются как булевы функции, зависящие от булевых переменных s(t) и x(t).
Шаг 1. Поиск в формуле подформул, которые могут быть реализованы некоторыми функциональными элементами. Изображение их на схема.
Шаг 2. Поиск подформул, аргументами которых могут являться функции, реализованные функциональными элементами на предыдущем шаге. Для найденных подформул реализующие их функциональные элементы изображаются на схеме. Совмещаются соответствующие входные и выходные узлы элементов.
Шаг 3. Шаг 2 повторяется до тех пор, пока не будут исчерпаны все формулы.
Пример. Построить схему для вычисления функции ![]()
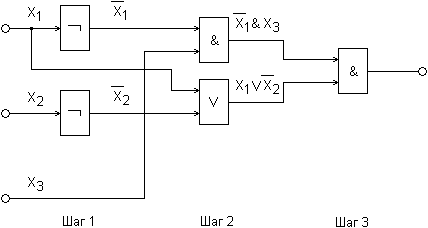
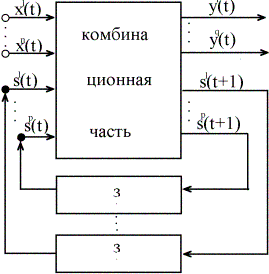
2 ЭТАП: Для сохранения значений состояний s(t+1) до следующего такта в схему вводится необходимое количество элементов памяти. Элемент, обеспечивающий запоминание одного бита двоичной информации в течение 2 такта, называется задержкой (триггером). На схеме такой элемент обозначается квадратом с буквой "з". Память содержит необходимое количество таких элементов.
Рекомендуемая учебная литература для изучения теории:
- Ерусалимский Я.М. Дискретная математика, теория, задачи.—М.: Вуз. кн., 1998.
- Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженеров.—М.: Энергоатомиздат, 1988.
- Логинов Б.М. Лекции и упражнения по курсу "Введение в дискретную математику".—Калуга, 1998.
- Мангушева И.П. и др. Ограниченно детерминированные функции и конечные автоматы.—Саратов: Изд–во СГУ, 1997.
- Нефедов В.Н., Осипова В.А. Курс дискретной математики: Учебное пособие.—М.: Изд–во МАИ, 1992.
- Оре О. Теория графов.—М.: Наука, 1980.
- Яблонский С.В. Введение в дискретную математику.—М.: Наука, 1986.
Рекомендуемые пособия для практических занятий:
- Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике.—М.: Наука, 1977.
- Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов.—М.: Наука, 1975.
- Макаров Р. Н. Практические занятия по дискретной математике. Учебное пособие.—Новосибирск: СибГУТИ, 2001.—56 с.: ил.
- Насыров З.Х. Дискретная математика. Учебное пособие.—Обнинск: ИАТЭ, 1999.