Введем понятия устойчивой и неустойчивой цепи. Цепь называется устойчивой, если свободные колебания с течением времени стремятся к нулю. В противном случае цепь называется неустойчивой. Из теории переходных процессов следует, что цепь является устойчивой, если корни характеристического уравнения лежат в левой полуплоскости комплексной переменной р. Если корни такого уравнения лежат в правой полуплоскости, то цепь является неустойчивой, т. е. она находится в режиме самовозбуждения. Таким образом, для определения условий устойчивости цепи достаточно найти характеристическое уравнение и его корни. Как видим, условия устойчивости можно определить и не вводя понятие обратной связи. Однако здесь возникает ряд проблем. Дело в том, что вывод характеристического уравнения и определение его корней являются громоздкой процедурой особенно для цепей высокого порядка. Введение понятия обратной связи облегчает получение характеристического уравнения или даже дает возможность обойтись без него. Крайне важно и то, что понятие обратной связи адекватно физическим процессам, возникающим в цепи, поэтому они становятся более наглядными. Глубокое понимание физических процессов облегчает работу по созданию автогенераторов, усилителей и т. д.

Рассмотрим цепь (см. рис. 14.2) и выведем ее характеристическое уравнение. Пусть u_вх(t) = 0 и, значит, U_вх(р) = 0. Тогда из (14.2) следует:

Здесь U_вых(р) ¹ 0 (в противном случае цепь нельзя считать возбужденной) и поэтому равенство (14.20) выполняется при условии

Если записать передаточную функцию основной цепи в виде (7.41): , а цепи ОС – , то уравнение (14.11) перепишется следующим образом:

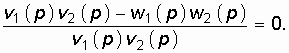
Это равенство выполняется при

Выражение в левой части этого равенства является полиномом, поэтому (14.22) можно записать в общем виде:

Это и есть характеристическое уравнение цепи.

Заметим еще раз, что точно такое же уравнение мы бы получили, составляя дифференциальное уравнение по законам Кирхгофа, как мы это делали при изучении переходных процессов.

Корни уравнения (14.23) в общем случае являются комплексными величинами

где p_k = a _k + jw _k. Зная корни характеристического уравнения, можно записать выходное напряжение:

Чтобы напряжение u_вых(t) не возрастало безгранично, всем корням p₁, p₂, ... , p_m характеристического уравнения необходимо иметь отрицательные вещественные части, т. е. корни должны располагаться в левой полуплоскости комплексной переменной р = = a + jw . Цепь с ОС, обладающая такими свойствами, называется абсолютно устойчивой.

При исследовании цепей с обратной связью могут возникать две проблемы. Если проектируемая цепь должна быть устойчивой, то необходимо располагать критерием, который по виду функций Н_у(р) и Н_ос(р) позволял бы судить об отсутствии корней характеристического уравнения в правой полуплоскости р. Если обратная связь используется для создания неустойчивой автоколебательной цепи, то следует убедиться, что корни уравнения (14.23) расположены, наоборот, в правой полуплоскости. При этом необходимо иметь такое расположение корней, при котором самовозбуждение происходило бы на требуемой частоте.

Рассмотрим критерии устойчивости цепи с обратной связью.

Критерий устойчивости Рауса — Гурвица

Он относится к алгебраическим критериям устойчивости и позволяет по значениям коэффициентов b_т, b_т–1, ..., b₀ характеристического уравнения (14.23), без определения его корней, узнать является ли исследуемая цепь устойчивой.

Критерий формулируется следующим образом: цепь с обратной связью является устойчивой, если полином характеристического уравнения, является полиномом Гурвица. При этом используется основное свойство полинома Гурвица: все его корни находятся в левой полуплоскости комплексной переменной р.

Для того, чтобы многочлен являлся полиномом Гурвица, необходимо и достаточно, чтобы были положительными определитель Рауса—Гурвица:

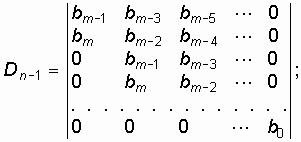
и все главные миноры этого определителя.

При составлении определителя Гурвица можно руководствоваться следующим правилом. В первой строке записываются коэффициенты полинома Гурвица через один, начиная со второго. Во второй строке записываются коэффициенты полинома через один, начиная с первого. Вторая пара строк формируется путем смещения первой пары строк на одну позицию. Третья пара — смещением второй пары строк еще на одну вправо и т. д.

Пример. Проверим с помощью критерия Рауса—Гурвица устойчивость цепи с обратной связью, характеристическое уравнение которой имеет вид

1. Составляем определитель Рауса—Гурвица

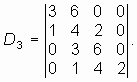
Главные миноры получаем вычеркиванием правого столбца и нижней строки из определителя или предыдущего минора:

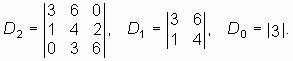
2. Вычисляем определитель Рауса—Гурвица и его главные миноры. Расчет удобно проводить в следующем порядке:

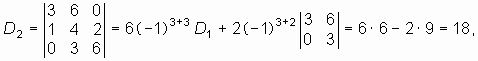
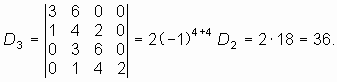
Определитель Рауса—Гурвица и его главные миноры положительны. Таким образом, цепь с ОС устойчива.

Критерий устойчивости Найквиста

Критерий Найквиста позволяет судить об устойчивости цепи с обратной связью по свойствам разомкнутой цепи (рис. 14.3, а).

Передаточная функция разомкнутой цепи, или петлевое усиление, входит в характеристическое уравнение (14.21):

Если найдется такая частота w , для которой конец вектора H_р(jw ) попадает в точку с координатами (1,j0), то это будет означать, что выполняется условие (14.25), т. е. на этой частоте в цепи произойдет самовозбуждение. Значит, по годографу можно определить, устойчива цепь или нет. Для этого используется критерий Найквиста, который формулируется следующим образом: если годограф передаточной функции разомкнутой цепи не охватывает точку с координатами (1, j0), то при замкнутой цепи обратной связи цепь является устойчивой. В том случае, когда годограф H_р(w ) охватывает точку (1, j0), цепь неустойчива. На рис. 14.4 показаны годографы трех цепей с положительной обратной связью (цифра 1 соответствует годографу устойчивой цепи).

Пользуясь критерием Найквиста, легко получить условия самовозбуждения цепи с ОС. Запишем выражение для H_р(jw ) в виде

где – модули передаточных функций; , – фазовые сдвиги соответственно в основном элементе и в цепи ОС.

Условия пересечения годографом оси абсцисс Re[H_р(jw )] при |H_р(jw )| 1 можно записать в виде двух условий:

1) условие (уравнение) баланса фаз , где п = 0, 1, 2,...;

2) амплитудное условие

Выполнение неравенства соответствует режиму возникновения колебаний с нарастающей амплитудой, что характерно для начального этапа самовозбуждения. Выполнение равенства H_у(w )´ ´ H_ос(w ) = 1 соответствует режиму генерации гармонического напряжения на частоте w с постоянной амплитудой и носит название баланса амплитуд.

Как будет показано ниже, уравнение баланса фаз позволяет определить частоту, на которой происходит самовозбуждение цепи с ОС, а уравнение баланса амплитуд дает возможность определить величину амплитуды u_вых(t) генерируемого колебания в стационарном режиме.

Пример. Исследуем устойчивость цепи, изображенной на рис. 14.8, a, В ней можно выделить усилительный элемент с передаточной функцией Н_у = К и цепь обратной связи (рис. 14.8, г) с передаточной функцией (14.17)

где t = RC.

Кроме того, напомним, что на усилитель сигнал поступает через входную цепь (рис. 14.8, в), передаточная функция которой (см. (14.16))

Получим характеристическое уравнение цепи:

или

.

Откуда окончательно получаем

Корни характеристического уравнения (14.16)

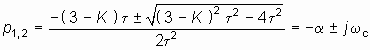
зависят от коэффициента усиления усилителя К. Расположение корней p₁ и p₂ на плоскости комплексного переменного р для разных коэффициентов усиления и соответствующие этому графики свободных колебаний в цепи показаны на рис. 14.10.

Устойчивость данной цепи можно исследовать и с помощью критерия Найквиста. Комплексная передаточная функция разомкнутой цепи равна

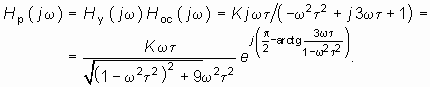
На рис. 14.4 приведены годографы H_р(jw ) устойчивой (К = 2, кривая 1) и неустойчивой (К = 3, кривая 2; К = 4, кривая 3) цепи.

Критерий устойчивости Михайлова

Этот простой и эффективный критерий был предложен в 1938 г. А.В. Михайловым и базируется он на характере поведения аргументов полинома Гурвица v(jw ) при изменении частоты w от нуля до бесконечности.

Положим, что полином Гурвица степени m

имеет l пар комплексно-сопряженных корней с отрицательной вещественной частью . Остальные m—2l корней – вещественные отрицательные числа: . Если учесть при этом, что произведение линейных множителей двух комплексно-сопряженных корней равно

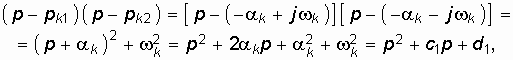
где

то полином Гурвица (14.27) можно разложить на следующие линейные множители

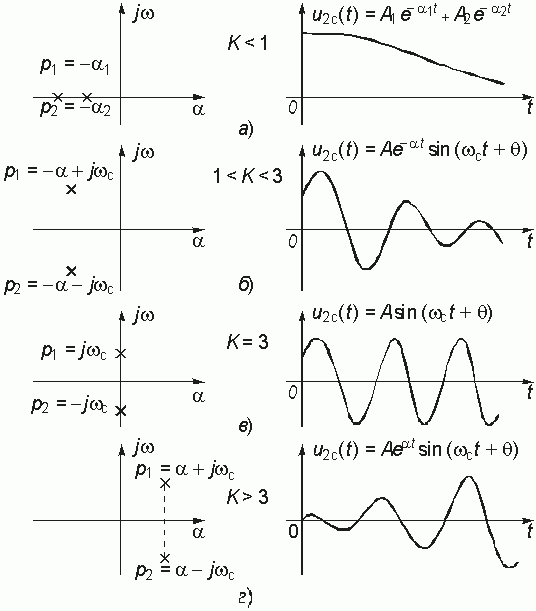
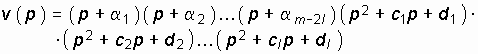
или далее полагая, что p = jw , получим

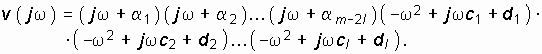
Как комплексную величину (14.28) можно представить в показательной форме

где

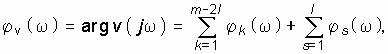
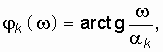
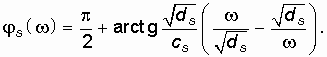
Как следует из (14.29), (14.30), (14.31) с увеличением w от 0 до ¥ монотонно возрастает от 0 до mp / 2. Это свойство аргумента полинома Гурвица и лежит в основе критерия Михайлова, который формулируется следующим образом: если при изменении частоты w от 0 до ¥ аргумент полинома Гурвица возрастает на угол mp / 2 (где m – степень полинома), то цепь будет устойчивой.

Действительно, если среди корней v(p) есть хотя бы один вещественный положительный корень, то в слагаемом типа (14.30) появится слагаемое и поэтому согласно (14.30) < mp / 2.

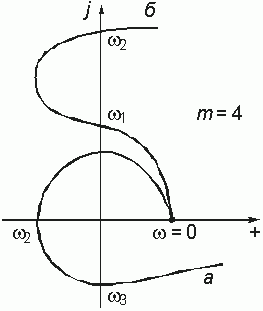
Критерий Михайлова имеет простой геометрический смысл: годограф v(jw) устойчивой цепи при изменении w от 0 до ¥ будет последовательно обходить в положительном направлении (против часовой стрелки) m квадрантов комплексной плоскости. На рис. 14.11 получены годографы устойчивой – а и неустойчивой – б цепи 4-го порядка:

В первом случае годограф v(jw) обходит 4 квадранта монотонно (последовательно) против часовой стрелки, при этом аргумент возрастает до величины

= 4p / 2 = 2p .

Во втором случае неустойчивой цепи изменяется скачком от 2-го квадранта в 4-й, при этом .