6.1. Волновая и лучевая трактовки световых процессов

6.2. Апертура волоконного световода

6.3. Типы волоконных световодов

6.4. Критическая частота и длина волны волоконного световода

6.5. Затухание сигнала в волоконных световодах

6.1. Волновая и лучевая трактовки световых процессов

В отличие от обычных кабелей, обладающих электрической проводимостью оптические кабели имеют совершенно другой механизм передачи энергии, а именно посредствам токов смещения как и в радиоканалах. Отличие от радиоканалов состоит в том, что волна распространяется не в свободном пространстве, а концентрируется в самом объеме световода и передаётся по нему в заданном направлении.

Как известно, однако, свет имеет двойственную природу: волновую и лучевую (корпускулярную). Волновая теория света обосновывает, что все свойства света совпадают со свойствами электромагнитных колебаний очень высокой частоты (10¹⁴...10¹⁵ Гц). Волны подразделяются на классы и типы (рассмотрены в лекции № 3). Тип волны (мода) определяется сложностью структуры, т.е. числом максимумов и минимумов поля в поперечном сечении. Мода обозначается двумя числовыми индексами n и m ( и ). Индекс n обозначает число полных изменений поля по окружности световода, индекс m - число изменений поля по диаметру (см. рис. 1).

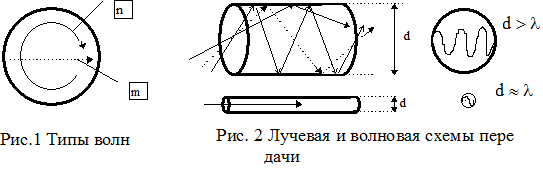
По корпускулярной теории свет - это поток быстро движущихся мелких частиц (корпускул), которые излучаются отдельными порциями (квантами) и образуют луч света.

Таким образом, теория света является синтезом волновых и лучевых его свойств. На рис 2 показана одномодовая и многомодовая схемы передачи. Одномодовой передачи соответствует один луч, а многомодовой - в данном примере три луча.

Передача волны по световоду осуществляется за счёт её отражения от границ сердцевины и оболочки, имеющих разные показатели преломления ( и , причем , см. рис.3), т.е. передача происходит волноводным методом.

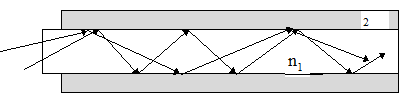
Рис.3

В волновой трактовке процесс передачи световых сигналов рассматривается как разновидность распространения ЭМ волн. Математические решения получают из электродинамических решений уравнений Максвелла. Решение этих уравнений приводит к цилиндрическим функциям Бесселя для сердцевины и Ганкеля для оболочки. Эти решения являются наиболее точными, т.к. учитывают модовый состав пропускаемого излучения, Основной вывод который следует из результатов решения: в световодах могут существовать моды соответствующие только целым значениям числовых индексов n и m. Для инженерных расчетов использование решений на основе уравнений Максвелла затруднительно в виду сложности.

6.2. Апертура волоконного световода

Более подходящей в этом смысле является лучевая теория. По законам геометрической оптики на границе сердечник оболочка в общем случае присутствуют падающая волна под углом , отраженная и преломленная - (см. рис. 4,б).

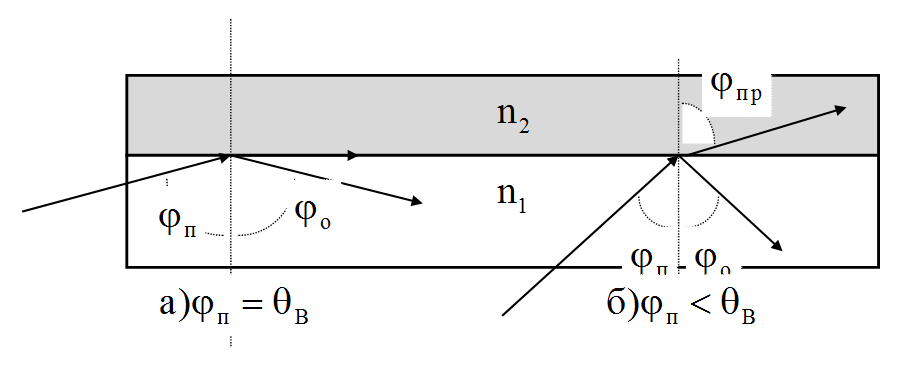
Рис. 4

Известно, что при переходе из среды с большей плотностью в среду с меньшей плотностью, т.е. при волна при определённом угле падения полностью отражается и не переходит в другую среду (рис. 4, а). Угол падения , начиная с которого вся энергия отражается от границы раздела сред, (т.е. ), называется углом полного внутреннего отражения:

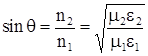, где (6.1)

, и - соответственно магнитная и диэлектрическая проницаемость сердечника и оболочки. (Исходим из общей формулы:

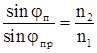, очевидно при получим соотношение (6.1))

Апертура волоконного световода - это угол между оптической осью и одной из образующих светового конуса, попадающего в торец волоконного световода, при котором выполняется условие полного внутреннего отражения (рис. 5).

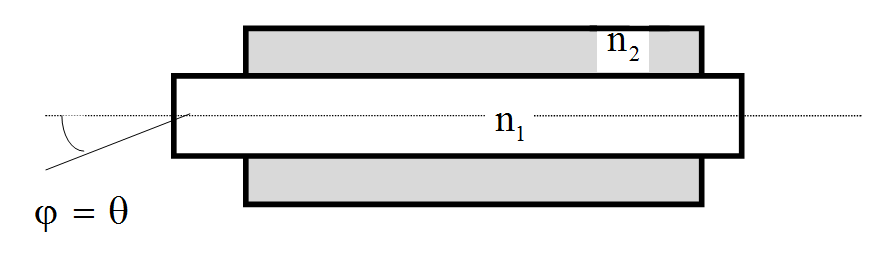
Рис. 5

Кроме этого часто используют понятие числовой апертуры (NA), которую определяют по формуле

,

где n_0, n₁ n₂ - показатели преломления наружной среды, сердцевины и оболочки. (если наружная среда - воздух n₀=1).

6.3. Типы волоконных световодов

Оптические волокна классифицируются на две группы: одномодовые и многомодовые, причем последние подразделяются на ступенчатые и градиентные.

В одномодовых оптических волокнах диаметр сердцевины соизмерим с длиной волны, и по нему передается всего один луч - тип волны (мода). В многомодовых оптических волокнах диаметр сердцевины больше, чем длина волны, и по нему распространяется большое число лучей (мод). Практически у одномодовых волокон диаметр сердцевины составляет мкм, а у многомодового - 50мкм.

Как видно из рис.6:а,б,в ход лучей у различных оптических волокон различен.

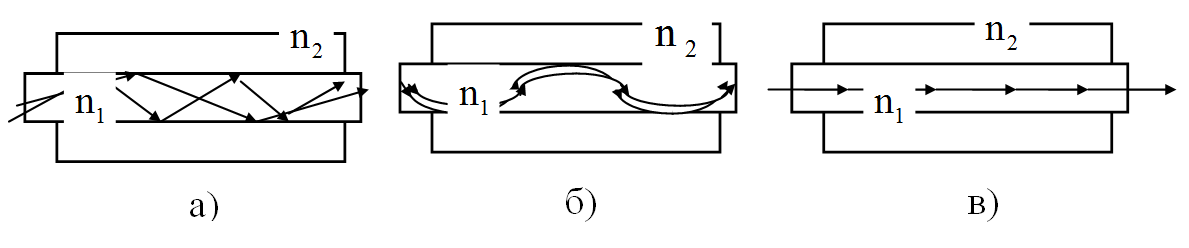
Рис. 6

В ступенчатом многомодовом волокне (а) лучи резко отражаются от от границы сердцевина - оболочка. Причем пути следования различных лучей различны и потому они приходят к концу линии со сдвигом во времени. Это приводит к искажению передаваемого сигнала (дисперсии).

В градиентном многомодовом волокне лучи распространяются по волнообразным траекториям и потому они с меньшим разбросом приходит к концу линии.

Наилучшими характеристиками в этом смысле обладает одномодовое волокно, т.к. здесь распространяется всего один луч.

Характер распространения лучей в многомодовом волокне определяется характером изменения коэффициента преломления по сечению волокна. В варианте (а) он резкий (ступенчатый). В варианте (б) плавный, например, по параболическому закону.

6.4. Критическая частота и длина волны волоконного световода

При фиксированном диаметре d световода и различных длинах волн характеристикой условий распространения излучения может быть некоторый угол , связанный соотношением:

. (6.2)

Как видно из рис.7, чем ближе длина волны к диаметру световода, тем меньше продольная составляющая распространения волны. Предельный случай . В соответствии с лучевой теорией при этом вдоль световода нет передачи энергии.

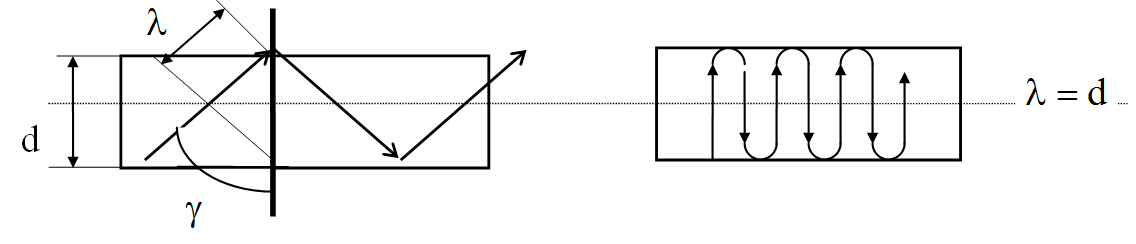
Рис. 7

Имея в виду, что и предполагая, что выполняется условие полного внутреннего отражения, т.е. можно записать

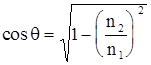. (6.3)

Прировняв правые части выражений (6.2) и (6.3) для косинусов получим:

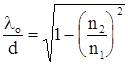. (6.4)

Критическая длина волны волоконного световода, в таком случае

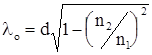. (6.5)

Соответственно критическая частота

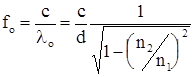, (6.6)

где - скорость распространения волны в сердечнике световода (сорость света).

Анализируя полученные соотношения, отметим, что чем толще сердечник световода и чем больше различаются и , тем больше критическая длина волны и соответственно ниже критическая частота. (Следует иметь в виду, что соотношения (6.5) и (6.6) получены из упрощенных выражений геометрической оптики и не учитывают возможность передачи по световоду большого числа различных типов волн. Более строгое решение может быть получено только на основе уравнений электродинамики.)

Ещё одной характеристикой световодов служит, так называемая, нормированная частота

, (6.7)

которая является обобщенной характеристикой световода.

Выбирая параметры световода таким образом, чтобы передаваемая частота была близка к критической, можно реализовать одномодовый режим распространения волны . Относительно нормированной частоты это условие может быть реализовано при V<2.405.

С увеличением диаметра сердцевины и уменьшением длины волны число мод резко возрастает. Число мод может быть приближенно определено как .

Достоинство одномодовой передачи является широкая полоса передаваемых частот (несколько гигагерц). С увеличением числа мод полоса передаваемых частот сужается. Однако одномодовый режим требует применение когерентных источников излучения (лазеров). Для многомодовых систем можно использовать простейшие источники излучения - светодиоды.

6.5. Затухание сигнала в волоконных световодах

Важнейшим параметром волоконного световода являются затухание. Затухание в волоконых световодах обусловлено потерями поглощения , рассеяния , и дополнительными кабельными потерями :

. (6.8)

Затухание в результате поглощения связано с потерями на диэлектрическую поляризацию, линейно растет с частотой, существенно зависит от свойств материала световода () и определяется по формуле (размерность Нп/км)

, (6.9)

- показатель преломления сердцевины;

- длина волны;

- тангенс угла диэлектрических потерь.

Потери рассеяния обусловлены неоднородностью материала волоконного световода и тепловой флюктуацией показателя преломления. В природе различают два механизма рассеяния Ми - рассеяние на неоднородностях значительно превышающих длину волны излучения и релеевское рассеяние - на неоднородностя соизмеримых с длиной волны излучения. В световдах основным является релеевское рассеяние, потери за счет которого определяются по формуле

, (6.10)

где - коэффициент рассеяния, для кварца равный 0.8 (мкм⁴дБ/км).

Потери на рэлеевское рассеяние определяют нижний предел потерь присущих волоконным световодам.

Реальные световоды на основе кварцевого стекла имеют ярко выраженую волновую зависимость потерь. Наименьшие потери соответствуют диапазонам волн 0.83мкм, 1.3мкм и 1.5мкм, которые получили названия окон прозрачности. Потери в окнах прозрачности ориентировочно составляют: 0.83мкм - 3 дБ/км; 1.3мкм - 1дБ/км; 1.5мкм - 0.3дБ/км.

Дополнительные кабельные потери обусловлены прежде всего причинами, связанными с технологией производства и эксплуатации волокна. Потери растут за счет скрутки, изгиба, отклонения от прямолинейности, из-за термомеханических воздействий при наложении оболочек и покрытий и др. факторами. Установлено, что дополнительные кабельные потери могут привести к увеличению затухания в два три раза.

Эффективное использование оптического волокна на основе кварцевого стекла ограничивается диапазоном 1.5мкм. Для более длинных волн кварц становится не прозрачным т.к. резко возрастают потери на поглощение. Поэтому для этого диапазона волн необходимо использовать новые материалы. Перспективными считаются фториды, галоиды и халькогениды. Например, в дальнем ИК диапазоне (10.6мкм) использование халькогенидов позволит достичь затухания порядка дБ/км, что даст возможность отказаться от ретрансляционных пунктов для линий практически любой длины в земных измерениях.