Пример аналоговой цепи дан на рис. 6. Сигнал на ее выходе находят из интеграла свертки (наложения) по входному сигналу и импульсной характеристике. Формула интеграла свертки описывается выражением (1). Это выражение можно назвать математической моделью аналоговой цепи.
При переходе к дискретным сигналам используют выражение дискретной свертки (2). Обозначим в этом выражении
![]() .
.
Тогда оно запишется в виде
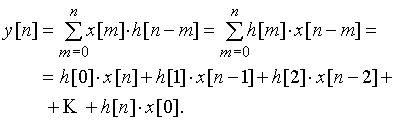 (17)
(17)
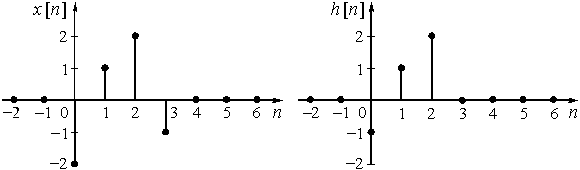
Рис. 28
Пример 12.1. Рассчитаем значения выходной последовательности ![]() цепи, имеющей дискретную импульсную характеристику
цепи, имеющей дискретную импульсную характеристику ![]() = {-1; 1; 2}, если входная последовательность имеет вид
= {-1; 1; 2}, если входная последовательность имеет вид ![]() = {-2; 1; 2: -1}. Графики
= {-2; 1; 2: -1}. Графики ![]() и
и ![]() приведены на рис. 28.
приведены на рис. 28.
Пользуясь формулой (17), рассчитаем значения выходной последовательности ![]()
![]()
![]()
![]()
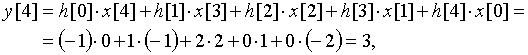
![]()
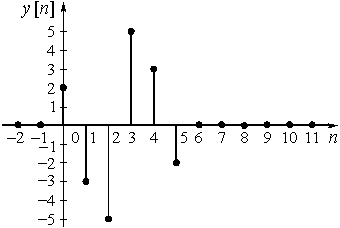
Рис. 29
График дискретного сигнала ![]() приведен на рис. 29.
приведен на рис. 29.
Вычисления по формуле (17) можно выполнить также с помощью простого устройства. Запишем последовательности чисел ![]() и
и ![]() на отдельных полосках бумаги, как показано на рис. 30. На обеих полосках пометим маленькими стрелочками точки n = 0. Обратим внимание на то, что
на отдельных полосках бумаги, как показано на рис. 30. На обеих полосках пометим маленькими стрелочками точки n = 0. Обратим внимание на то, что ![]() является обратной последовательностью относительно
является обратной последовательностью относительно ![]() , так что она строится в обратном направлении от n = 0. Будем сдвигать нижнюю полоску относительно верхней в направлении стрелки. Вычисление суммы произведений стоящих друг против друга чисел при каждом сдвиге дает последовательность
, так что она строится в обратном направлении от n = 0. Будем сдвигать нижнюю полоску относительно верхней в направлении стрелки. Вычисление суммы произведений стоящих друг против друга чисел при каждом сдвиге дает последовательность ![]() .
.
Если в качестве чисел ![]() взять дискретные значения
взять дискретные значения ![]()
![]() , то выражение (17) будет являться дискретной математической моделью аналоговой RC-цепи, изображенной на рис. 6. Выбирая те или иные значения
, то выражение (17) будет являться дискретной математической моделью аналоговой RC-цепи, изображенной на рис. 6. Выбирая те или иные значения ![]() , получим дискретные модели различных цепей. Таким образом, формула дискретной свертки является универсальной, пригодной для описания любых цепей.
, получим дискретные модели различных цепей. Таким образом, формула дискретной свертки является универсальной, пригодной для описания любых цепей.

Рис. 30
Пример 12.2. На вход цепи поступает сигнал в виде дискретной d-функции. Рассчитаем выходные последовательности ![]() цепей, имеющих дискретные импульсные характеристики
цепей, имеющих дискретные импульсные характеристики
а) ![]() = {1; 1; 0; 0; ...};
= {1; 1; 0; 0; ...};
б) ![]() = {1; -1; 0; 0; ...};
= {1; -1; 0; 0; ...};
в) ![]() .
.
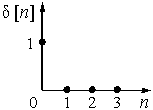
Рис. 31
Графики дискретной d-функции ![]() и импульсных характеристик а), б), в) приведены на рис. 31 и рис. 32 соответственно.
и импульсных характеристик а), б), в) приведены на рис. 31 и рис. 32 соответственно.
Рассчитываем значения ![]() , используя формулу (17)
, используя формулу (17) ![]()
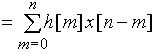 , в которой
, в которой ![]() =
= ![]() = {1; 1; 0; 0; ...}.
= {1; 1; 0; 0; ...}.
Для цепи, имеющей дискретную импульсную характеристику
а) ![]() = {1; 1; 0; 0; ...}, получаем
= {1; 1; 0; 0; ...}, получаем
![]()
![]()
![]()
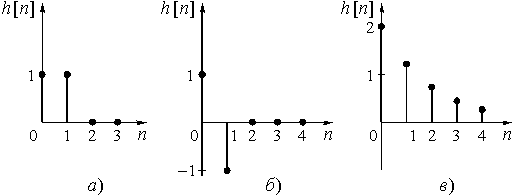
Рис. 32
![]()
Все остальные значения ![]() будут также нулевыми.
будут также нулевыми.
Для цепи с импульсной характеристикой
б) ![]() = {1; -1; 0; 0; ...} получаем
= {1; -1; 0; 0; ...} получаем
![]()
![]()
![]()
Остальные значения ![]() равны нулю.
равны нулю.
Для цепи с импульсной характеристикой
в) ![]() = {2; 1,22; 0, 74; 0,45; 0,27; ...} получаем
= {2; 1,22; 0, 74; 0,45; 0,27; ...} получаем
![]()
![]()
![]()
Все остальные отсчеты выходной последовательности ![]() повторяют соответствующие отсчеты дискретной импульсной характеристики
повторяют соответствующие отсчеты дискретной импульсной характеристики ![]() , также как и в двух предыдущих случаях а) и б). Этот вывод очевиден, т.к. импульсная характеристика - это реакция цепи на d-импульс.
, также как и в двух предыдущих случаях а) и б). Этот вывод очевиден, т.к. импульсная характеристика - это реакция цепи на d-импульс.
Графики ![]() будут такими же, как графики
будут такими же, как графики ![]() на рис. 32.
на рис. 32.
Анализ формулы (17) показывает, что в ней выполняется всего три действия: умножение, сложение и задержка. На рис. 33 эти действия представлены в виде элементов структурной схемы. Операцию умножения дискретного сигнала ![]() на число К можно представить в виде усилителя с коэффициентом усиления К. На его выходе получаем сигнал
на число К можно представить в виде усилителя с коэффициентом усиления К. На его выходе получаем сигнал ![]() . Сложение чисел естественно отобразить на схеме в виде сумматора. Получение отсчета
. Сложение чисел естественно отобразить на схеме в виде сумматора. Получение отсчета ![]() из
из ![]() можно связать с задержкой последнего на время Т, т.е. на один «такт».
можно связать с задержкой последнего на время Т, т.е. на один «такт».
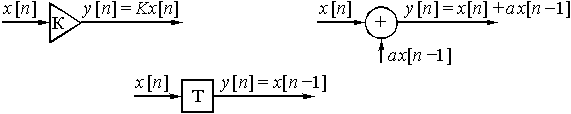
Рис. 33
Действие элемента задержки поясняется на рис. 34.
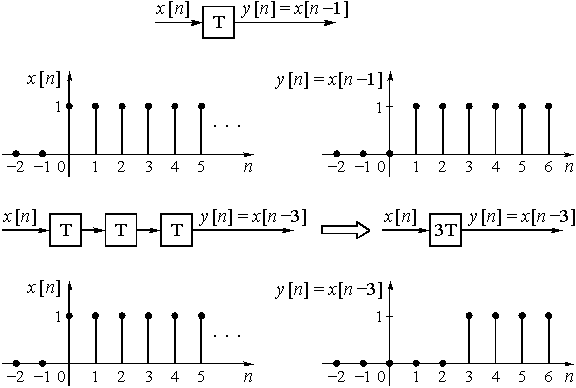
Рис. 34
Алгоритм вычислений дискретного сигнала ![]() , описываемый выражением (17), можно представить в виде структурной схемы. Подобные структурные схемы называют дискретными цепями.
, описываемый выражением (17), можно представить в виде структурной схемы. Подобные структурные схемы называют дискретными цепями.
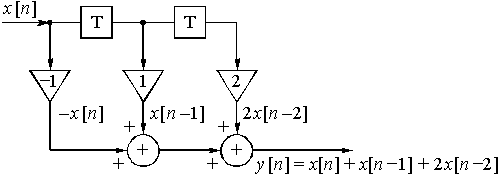
Рис. 35
Пример 12.3. Составим структурную схему цепи, дискретная импульсная характеристика которой дана в задаче 12.1, т.е. ![]() = {-1; 1; 2} (рис. 28).
= {-1; 1; 2} (рис. 28).
В соответствии с алгоритмом (17) и с учетом заданных значений характеристики ![]() структурная схема цепи приведена на рис. 35. По этой схеме несложно определить выражение для выходной последовательности
структурная схема цепи приведена на рис. 35. По этой схеме несложно определить выражение для выходной последовательности ![]()
![]() .
.
Вывод: в отличие от аналоговых цепей, которые представляют собой соединение элементов, например, R, L и С, дискретная цепь - это структурная схема алгоритма вычислений выходной последовательности по входной. Она состоит из элементов задержки, сумматоров и усилителей (умножителей).
Самоконтроль
1. В чем отличие импульсных характеристик дискретных и аналоговых цепей?
2. Как вычисляются значения выходной последовательности дискретной цепи?
3. Какие дискретные элементы используются для реализации алгоритма дискретной свертки?
4. Как работает элемент задержки? Приведите структурную схему цепи, на вход которой подается дискретный сигнал ![]() , а на выходе сигнал
, а на выходе сигнал ![]() .
.
5. Составьте структурные схемы дискретных цепей, имеющих дискретные импульсные характеристики, приведенные в примере 12.2, а и 12.2, б.
6. Запишите общие выражения выходных последовательностей ![]() для каждой из дискретных цепей, полученных в предыдущем пункте 5.
для каждой из дискретных цепей, полученных в предыдущем пункте 5.

