В цифровой системе коммутации каждый сигнал X_iI передается по ифровому каналу k_i , принадлежащему определенному тракту R , т.е.

X_i ® k_i , k_i Î R , i = . (1)

Число каналов n в тракте определяется мощностью используемой системы передачи. В общем случае мощность входящих и исходящих цифровых трактов n_пер не равна мощности внутристанционных цифровых трактов системы коммутации n_комм , причем возможны различные соотношения:

n_пер < n_ком , n_пр > n_ком , n_nep = n_ком , (2)

которые определяются рядом факторов, в том числе обеспечением необходимых коммутационных возможностей системы.

Координаты каждого цифрового канала k_i как объекта коммутации определяются двумя координатами:

• временной, определяемой номером временного интервала t_i , отводимого каналу k_i - в общем, цикле передачи системы Т;
• пространственной , определяемой номером S_i цифрового тракта, которому принадлежит данный канал.

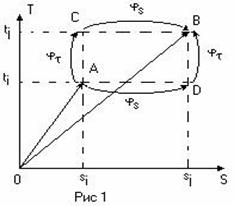
Таким образом, имеем векторное представление канала: k_i - { S_i,, t_i } в двухкоординаторном пространстве S и Т (рис. I). Коммутация цифровых каналов - это процесс образования соединительного тракта в простейшем случае двух цифровых каналов:

k_i(S_i,, t_i) « k_j(S_j,, t_j) (3)

Поскольку координаты S и Т, определяющие цифровые каналы, - ортогональны, то, следовательно, процесс коммутации Æ разбивается на 2 класса процессов:

j_s - преобразование пространственной координаты канала, т.е. пространственная коммутация;

j_r - преобразование временной координаты канала, т.е. временная коммутация.

Последовательность процессов преобразования каждой координаты, а также число этапов преобразования каждого вида может быть различной, но каждой из них соответствует определенный класс структур коммутационных полей. В табл. I приведены некоторые из них.

Таблица I