В однородном канале связи условные(переходные) вероятности p(y1/x1) не зависят от времени. Граф состояний и переходов однородного двоичного канала связи приведен на рис. 8.

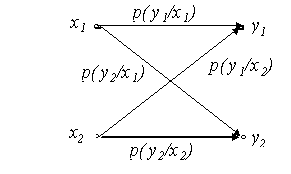
Рис.8

На этом рисунке x1 и x2 – сигналы на входе канала связи, y1 и y2 – сигналы на выходе. Если передавался сигнал x1 и принят сигнал y1, это означает, что первый сигнал (индекс 1) не исказился. Если передавался первый сигнал (x1), а принят второй сигнал (y2), это означает, что произошло искажение первого сигнала. Вероятности переходов указаны на рис. 7. Если канал симметричный, то вероятности переходов попарно равны.

Обозначим :

p(y2/x1)= p(y1/x2)=pэ – вероятности искажения элемента сигнала,

p(y1/x1)= p(y2/x2)=1-pэ – вероятности правильного приёма элемента сигнала.

В соответствии с формулами (21) и (23)

.

Если сигналы x1 и x2 имеют одинаковую длительность tэ, то . Тогда пропускная способность канала будет равна

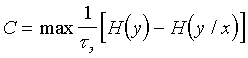. (27)

В этой формуле maxH(y)=logk. Для двоичного канала (k=2) maxH(y)=1 и формула (24) примет вид

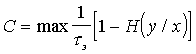. (28)

Остаётся определить условную энтропию H(y/x). В соответствии с (19) для двоичного источника имеем

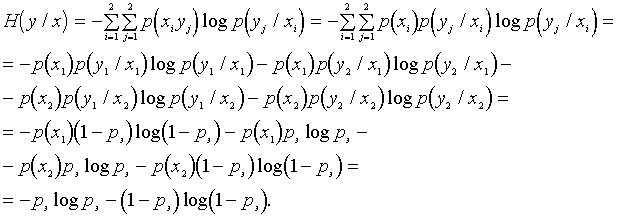
Подставив это значение условной энтропии в (28), получим окончательно

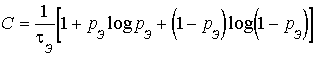. (29)

C, бит/с

Для канала связи с k>2 пропускная способность определяется почти аналогичной формулой:

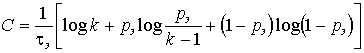. (30)

В заключении рассмотрим один пример. Пусть имеется двоичный источник с производительностью 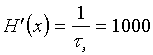бит/c.

Если вероятность искажения pэ=0,01, то из этого следует, что из 1000 элементов сигнала, переданных за одну секунду, в среднем 990 элементов будут приняты без искажений и только 10 элементов будут искажены. Казалось бы, пропускная способность в этом случае будет составлять 990 бит в секунду. Однако вычисление по формуле (29) даёт нам величину, значительно меньшую (C=919 бит/с). В чём здесь дело? А дело в том, что мы получили бы C=990 бит/с, если бы точно знали, какие именно элементы сообщения искажены. Незнание этого факта (а это практически знать невозможно) приводит к тому, что 10 искажённых элементов настолько сильно снижают ценность принимаемого сообщения, что пропускная способность резко уменьшается.

Другой пример. Если pэ=0,5, то из 1000 переданных элементов 500 не будут искажены. Однако теперь уже пропускная способность будет составлять не 500 бит/с, как можно было бы предполагать, а формула (29) даст нам величину C=0. Действительно при pэ=0,5 сигнал по каналу связи фактически уже не проходит и канал связи просто эквивалентен генератору шума.

При pэ>1 пропускная способность приближается к максимальной величине. Однако в этом случае сигналы на выходе системы связи необходимо инвертировать.

Вопросы

1. От чего зависит пропускная способность дискретного канала связи с помехами?
2. Как определяется пропускная способность дискретного канала связи с помехами?
3. Как влияют помехи на величину пропускной способности канала связи?
4. Чему равна пропускная способность двоичного канала связи при вероятности искажения элемента сообщения, равной 0,5?