Модуляция – это процесс изменения во времени значений одного или нескольких параметров несущего ВЧ колебания – амплитуды, частоты или фазы - в соответствии с изменениями передаваемого сигнала (сообщения). При простых видах модуляции модулирующее сообщение изменяет только один параметр – как правило, фазу. При комбинированных видах модуляции (или при плохой схемотехнической реализации простых схем) одновременно могут изменяться амплитуда и фаза несущей. Высокая помехоустойчивость, энергетическая эффективность и экономное расходование полосы частот современных СПРС достигаются в значительной степени благодаря рациональному выбору параметров модуляции.

Общая модель процессов, происходящих в модуляторе, характеризует все типы модуляций и описывается формулой

где Re{∙} - действительная часть комплексного аргумента, а функция x(t) = х^I(t) + jx^Q (t); при этом х^I(t) и x^Q(t) - сигналы, модулирующие косинусоидальную и синусоидальную составляющие несущей с частотой f_c. При соответствующем выборе этих сигналов можно описать любую цифровую модуляцию. В широко распространенной квадратурной модуляции выходной сигнал образуется суммированием двух различных модулированных сигналов, несущие которых имеют между собой фазовый сдвиг 90°. Модулирующие сигналы называются соответственно синфазной (I) и квадратурной (Q) составляющими.

В СПРС предъявляются весьма жесткие требования к типу используемой модуляции. Прежде всего речь идет о спектральной эффективности сигналов, которая зависит, в конечном счете, от компактности их спектра - относительной величины мощности, сосредоточенной в главном лепестке спектра, то есть в полосе частот по первым "нулям" спектра, равной 2/t_с, где t_с – длительность сигнала (время, затрачиваемое на передачу одного бита информации). В главном лепестке спектра сигнала после модуляции должно находиться не менее 94…97% всей энергии сигнала. Часто предъявляют высокие требования к скорости убывания составляющих спектра при больших расстройках за пределами главного лепестка спектра. Увеличение скорости спадания внеполосного излучения (ВПИ) обеспечивает непрерывность фазы сигнала в моменты перехода от символа к символу, поскольку скорость спадания ВПИ зависит от числа непрерывных производных текущей фазы сигнала.

Другое требование связано с необходимостью обеспечения постоянной огибающей сигнала и относится к возможности использования в подвижной станции нелинейного усилителя радиодиапазона, что особенно важно для энергетического бюджета подвижной станции.

Обратимся к схеме линейного модулятора для двукратной модуляции (рис. 16.1). Двоичный поток данных (приходящий, как правило, с выхода перемежителя) направляется на вход преобразователя, который преобразует блоки двоичной информации в пары (дибиты) информационных символов - d^I и d^Q. Эти информационные символы направляются на фильтры модулирующего сигнала с импульсной характеристикой р(t) и q(t). Сигналы, модулирующие синфазную и квадратурную составляющие, описываются формулами

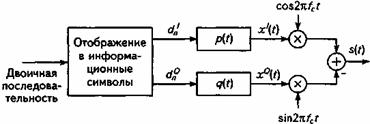
Рис. 16.1. Линейный модулятор для двукратной модуляции

При помощи этих формул можно описать различные типы линейных модуляций. Так, выбор значений q(t) = 0, d^I = ±1 и p(t) = rect (t/T) соответствует двухпозиционной ФМ-2, часто называемой двоичной фазовой манипуляцией (BPSK). При выборе значений — d^I = d^Q = ±1, a p(t) = q(t) = rесt(t/T) получим четырехпозиционную ФМ-4, называемую квадратурной фазовой манипуляцией (QPSK). Обычно число возможных состояний (позиций, уровней) модулируемого параметра обозначают через М. Число сигналов обычно кратно 2, т.е. М = 2 ^В и В = log₂ M ; здесь В - кратность модуляции (В = 2,…8).

Такие виды модуляции, как квадратурная амплитудная модуляция (QAM), у которых В ≥ 2, получаются путем выбора многоуровневых информационных символов d^I и d^Q. При М = 4 КАМ (4-QAM) совпадает с ФМ-4, однако при М > 8 эффективность квадратурной амплитудной модуляции выше. Стоит упомянуть, что КАМ до сих пор напрямую не применялась в системах подвижной связи, прежде всего, из-за непостоянства огибающей.

Благодаря использованию комплексного сигнала x(t) каждая модуляция представляется в виде набора характеристических точек на комплексной плоскости (так называемого созвездия), траектория которых характеризует движение во времени по комплексной плоскости сигнальной точки с координатами х^I(t), x^Q(t). Форма сигнального созвездия соответствует виду модуляции. Для адекватного отображения пространства сигналов на выходе квадратурного модулятора обычно используют прямоугольную систему координат, в которой по горизонтальной оси /, которая символизирует нулевой фазовый сдвиг, откладывают уровень сигнала в синфазном канале, а по вертикальной оси Q, символизирующей сдвиг на 90°, уровень сигнала в квадратурном канале. Сигналы отображаются точками, которые являются концами двумерных векторов на квадратурной (иначе - векторной) диаграмме.

На рис. 16.2 изображены созвездия нескольких наиболее важных цифровых модуляций. В случае М-позиционной ФМ М сигнальных точек располагаются на окружности с радиусом R =Ö E (Е - энергия посылки сигнала), на равных расстояниях d_M между точками созвездия с угловым интервалом 2п/М радиан. Расстояния d_M характеризуют помехоустойчивость при приеме сигнала. Так, максимально возможное значение d₂ =2Ö E соответствует максимальной (потенциальной) помехоустойчивости (т.е. наименьшей вероятности ошибочного приема), которой характеризуются т.н. противоположные (манипулированные по фазе на 180^о) сигналы ФМ-2 (рис. 16.2а). У двукратной ФМ-4 (рис. 16.2б) минимальное расстояние d₄ = Ö2E, что соответствует расстоянию между ортогональными сигналами. Эти сигналы являются наилучшими по помехоустойчивости из всех двумерных четырехпозиционных сигналов.

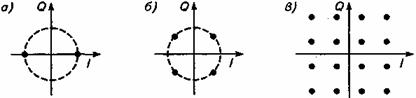
Рис. 16.2. Примеры сигнальных созвездий: а - BPSK, б - QPSK, в - 16-QAM

Сигналы с фазовой модуляцией обладают высокой помехоустойчивостью, однако у них невелика спектральная эффективность, да и с точки зрения систем подвижной связи такие сигналы обладают существенным недостатком - огибающая имеет переменный характер и может принимать мгновенные значения, близкие к нулю. Чтобы проиллюстрировать это, можно воспользоваться графиком траектории сигнала на I(Q) - диаграмме для всех возможных комбинаций дибитов (пар) входных символов (рис. 16.3). Такая траектория отображает всевозможные линии перехода между символами передаваемого потока, зависящие от его статистических свойств.

Главный лепесток спектра ФМ-4 (QPSK) содержит порядка 90% всей мощности сигнала, в результате чего эффективность использования спектра, показывающая, сколько бит в секунду информации можно передать в одном герце полосы, не превосходит 1,5 бит/с/Гц. При использовании ФМ-2 (или ФМ-4) определение фазы любой принятой посылки производится по отношению к некоторой фиксированной опорной фазе j_оп, вследствие чего реализация демодулятора таких сигналов сопровождается известными трудностями. С целью устранения этого недостатка используют относительное кодирование передаваемого сообщения на стороне передачи и относительное декодирование - на приемной стороне. Перекодирование исходной цифровой последовательности осуществляется по правилу: b_i = a_i Å b_i-1, где a_i - символ на входе относительного кодера; b_i - символ на его выходе; b_i-1 - символ с выхода кодера, задержанный на такт, т.е. на длительность t_с ; Å - процедура сложения по модулю 2.

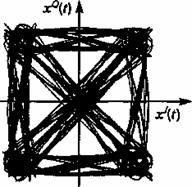
Рис. 16.3. Огибающая модуляции ФМ-4 (QPSK) на квадратурной плоскости

Перекодирование исходных данных и как следствие этого переход к сигналам ОФМ, естественно, не повышает эффективность использования спектра при их передаче по каналам связи. Универсальным средством уменьшения полосы, требуемой для передачи модулированных сигналов, является перехода к многократной (В>2) (многопозиционной) модуляции. При этом исходная последовательность символов разбивается на блоки по В = 2,3,4,…соседних символов (соответственно при М = 4,8,16,...), а длительность сигнала оказывается равной Т_с = t_с ´ В, что приводит к сокращению в В раз полосы занимаемых частот (при сохранении скорости передачи) и возрастанию приблизительно в В раз эффективности использования спектра.

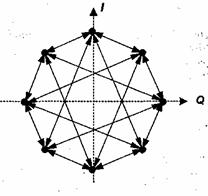
Рис. 16.4. Сигнальное созвездие модуляции p/4-ОФМ-4.

Для повышения спектральной эффективности широко применяется относительная квадратурная ОФМ-4 (DQPSK), а уменьшение изменений огибающей при манипуляции фазы у таких сигналов достигается добавлением фазового сдвига p/4 к дифференциальному сигналу в каждый период манипуляции (рис. 16.4). При реализации дифференциального кодирования в сочетании со сдвигом несущей на π/4 сигнальное созвездие формируется двумя четырехточечными созвездиями QPSK, наложенными со сдвигом 45°. В результате в сигнале присутствуют восемь фазовых сдвигов, причем фазы символов выбираются поочередно - то из одного созвездия QPSK, то из другого. Последовательные символы имеют относительные фазовые сдвиги (относительно предыдущего периода модуляции), соответствующие одному из четырех углов: ± π/4 и ±3 π/4. В результате огибающая не принимает мгновенные значения, равные нулю. Такая модуляция, обозначаемая p/4-ОФМ-4 (p/4-shift DQPSK), достаточно широко применяется в системах подвижной связи, например, в D-AMPS, PDC и ТЕТRА.

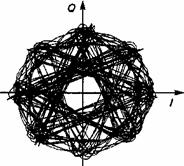
Рис. 16.5. Огибающая модуляции p/4-ОФМ-4 на квадратурной плоскости.

На рис. 16.5 изображены траектории сигнала p/4-ОФМ-4 для всех возможных комбинаций дибитов входных символов в случае, когда цифровые символы формируются модулирующим фильтром с характеристикой p(t) (см. рис.16.1) в виде корня квадратного из приподнятого косинуса и коэффициентом сглаживания, равным 0,35. Несмотря на то, что модуляция не обладает постоянной огибающей, ее колебания ограничены, и она никогда не достигает нуля. Это помогает бороться с нелинейными искажениями, вносимыми нелинейностью усилителей мощности подвижных станций.

Весьма эффективной является также частотная модуляция минимальным сдвигом ЧММС (MSK), которая способна обеспечить минимум помех в соседних по частоте каналах. Этот метод представляет собой частотную манипуляцию, при которой несущая частота дискретно – через интервалы времени, кратные периоду Т = t_с битовой модулирующей последовательности, принимает значения f_н = f₀ – F/4 или f_в = f₀ + F/4, где f₀ – центральная частота используемого частотного канала, а F = 1/T. Метод MSK иногда рассматривают как метод квадратурной фазовой манипуляции со смещением (офсетная OQPSK), но с заменой прямоугольных модулирующих импульсов длительности 2Т полуволновыми отрезками синусоид или косинусоид. Разнос частот Df = f_в - f_н = F/2 - минимально возможный, при котором обеспечивается ортогональность колебаний частот f_н и f_в на интервале Т длительности одного бита; при этом за время Т между колебаниями частот f_н и f_в набегает разность фаз, равная p. Таким образом, термин "минимальный сдвиг" в названии метода модуляции относится, в указанном выше смысле, к сдвигу частоты. Поскольку модулирующая частота в этом случае равна F/2, а девиация частоты F/4, индекс частотной модуляции составляет m = (F/4)/(F/2) = 0,5.

MSK реализуется в стандарте GSM как гауссовская манипуляция с минимальным сдвигом (GMSK). Термин «гауссовская» в названии метода модуляции соответствует дополнительной фильтрации модулирующей битовой последовательности относительно узкополосным гауссовским фильтром с импульсной характеристикой h(t); именно эта дополнительная фильтрация отличает метод GMSK от метода MSK. В качестве характеристического параметра GMSK используют произведение ВТ, где В - ширина спектра импульса h(t) по уровню З дБ, а Т- длительность одного бита. На рис. 16.6 изображена спектральная плотность мощности на выходе идеального GMSK-модулятора (ВТ = 0,3), нормализованного по отношению к периоду Т. Сравнение этого графика со спектральной плотностью мощности MSK и BPSK, указывает на серьезное преимущество этой модуляции, прежде всего - в части скорости спадания внеполосного излучения, т.е. скорости снижения уровня мощности боковых спектральных лепестков.

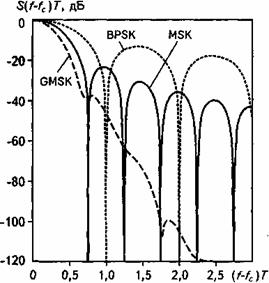
Рис. 16.6. Спектральная плотность мощности сигнала GMSK в сравнении с сигналами MSK и BPSK