6.7.1. Алгебраическая структура циклических кодов
6.7.2. Свойства двоичного циклического кода
6.7.3. Кодирование в систематической форме
6.7.4. Логическая схема для реализации полиномиального деления
6.7.5. Систематическое кодирование с (n-k)-разрядным регистром сдвига
6.7.6. Обнаружение ошибок с помощью (n-k)-разрядного регистра сдвига
Важным подклассом линейных блочных кодов являются двоичные циклические коды (cyclic codes). Код легко реализуется на регистре сдвига с обратной связью; на подобных регистрах сдвига с обратной связью вычисляется синдром; алгебраическая структура циклического кода естественным образом позволяет эффективно реализовать методы декодирования. Итак, линейный код (n, k) называется циклическим, если он обладает следующим свойством. Если n-кортеж ![]() является кодовым словом в подпространстве S, тогда
является кодовым словом в подпространстве S, тогда ![]() , полученный из U с помощью циклического сдвига, также является кодовым словом в S. Или, вообще,
, полученный из U с помощью циклического сдвига, также является кодовым словом в S. Или, вообще, ![]() , полученный i циклическими сдвигами, является кодовым словом в S.
, полученный i циклическими сдвигами, является кодовым словом в S.
Компоненты кодового слова ![]() можно рассматривать как коэффициенты полинома
можно рассматривать как коэффициенты полинома ![]() .
.
![]() (6.54)
(6.54)
Полиномиальную функцию U(X) можно рассматривать как "заполнитель" разрядов кодового слова U, т.е. вектор n-кортежа описывается полиномом степени ![]() или меньше. Наличие или отсутствие каких-либо членов в полиноме означает наличие 1 или 0 в соответствующем месте n-кортежа. Если
или меньше. Наличие или отсутствие каких-либо членов в полиноме означает наличие 1 или 0 в соответствующем месте n-кортежа. Если ![]() -й компонент отличен от нуля, порядок полинома равен
-й компонент отличен от нуля, порядок полинома равен ![]() . Удобство такого полиномиального представления кодового слова станет более понятным по мере дальнейшего обсуждения алгебраических свойств циклических кодов.
. Удобство такого полиномиального представления кодового слова станет более понятным по мере дальнейшего обсуждения алгебраических свойств циклических кодов.
6.7.1. Алгебраическая структура циклических кодов
В кодовых словах, выраженных в полиномиальной форме, циклическая природа кода проявляется следующим образом. Если U(X) является кодовым словом, представленным полиномом порядка ![]() , то
, то ![]() — остаток от деления
— остаток от деления ![]()
![]() на
на ![]() — также является кодовым словом. Иными словами,
— также является кодовым словом. Иными словами,
![]() (6.55,a)
(6.55,a)
или, умножая обе части уравнения на ![]() ,
,
![]() , (6.55,б)
, (6.55,б)
что в модульной арифметике можно описать следующим образом.
![]() по модулю
по модулю ![]() (6.56)
(6.56)
Здесь "х по модулю у" означает остаток от деления х на у. Ниже справедливость выражения (6.56) демонстрируется для случая i = 1.
![]()
![]()
К последнему выражению прибавим и вычтем ![]() или, поскольку мы пользуемся арифметическими операциями по модулю 2, можем прибавить
или, поскольку мы пользуемся арифметическими операциями по модулю 2, можем прибавить ![]() дважды.
дважды.
![]()
Поскольку порядок ![]() равен
равен ![]() , этот полином не делится на
, этот полином не делится на ![]() . Таким образом, используя уравнение (6.55,а), можно записать следующее.
. Таким образом, используя уравнение (6.55,а), можно записать следующее.
![]() по модулю
по модулю ![]()
Обобщая, приходим к уравнению (6.56).
![]() по модулю
по модулю ![]()
Пример 6.7. Циклический сдвиг вектора кода
Пусть U = 1 1 0 1 для n = 4. Выразите кодовое слово в полиномиальной форме и, используя уравнение (6.56), выполните третий циклический сдвиг кодового слова.
Решение
![]()
![]() полином записан в порядке возрастания степени
полином записан в порядке возрастания степени
![]() , где
, где ![]()
Разделим ![]() на
на ![]() и найдем остаток, используя полиномиальное деление.
и найдем остаток, используя полиномиальное деление.
| X6 + X4 + X3 | X4 + 1 | ||
| X2 + 1 остаток U(3)(X) | |||
| X6 + X2 | + 1 | ||
| X4 + X3 + X2 X4 | |||
| X3 + X2 + 1 | |||
Записываем остаток в порядке возрастания степеней: 1 + X2 + X3, кодовое слово U=1011 представляет собой три циклических сдвига U= 1 1 0 1. Напомним, что для двоичных кодов операция сложения выполняется по модулю 2, так что + 1 = -1, и, следовательно, в расчетах знаки "минус" не отражены.
6.7.2. Свойства двоичного циклического кода
С помощью полиномиального генератора можно создать циклический код, почти так же как создавались блочные коды с использованием матрицы генератора. Полиномиальный генератор g(X) для циклического кода (n, k) является единственным и имеет следующий вид.
![]() (6.57)
(6.57)
Здесь ![]() и gp должны быть равны 1. Каждый полином кодового слова в подпространстве имеет вид
и gp должны быть равны 1. Каждый полином кодового слова в подпространстве имеет вид ![]() , где U(X) — полином степени
, где U(X) — полином степени ![]() или меньше. Следовательно, полином сообщения т(Х) будет иметь следующий вид.
или меньше. Следовательно, полином сообщения т(Х) будет иметь следующий вид.
![]() (6.58)
(6.58)
Всего в коде (n, k) существует ![]() полинома кодовых слов и
полинома кодовых слов и ![]() вектора кода. Поэтому на каждый вектор кода должен приходиться один полином кодового слова.
вектора кода. Поэтому на каждый вектор кода должен приходиться один полином кодового слова.
![]()
или
![]()
Отсюда следует, что g(X), как показано в уравнении (6.57), должен иметь степень ![]() , и каждый полином кодового слова в коде (п, k) можно выразить следующим образом.
, и каждый полином кодового слова в коде (п, k) можно выразить следующим образом.
![]() (6.59)
(6.59)
U будет считаться действительным кодовым словом из подпространства S тогда и только тогда, когда U(Х) делится на g(X) без остатка.
Полиномиальный генератор g(X) циклического кода (n,k) является множителем ![]() , т.е.
, т.е. ![]() . Например,
. Например,
![]()
Используя ![]() как полиномиальный генератор степени
как полиномиальный генератор степени ![]() , можно получить циклический код (n, k) = (7,4). Или же с помощью
, можно получить циклический код (n, k) = (7,4). Или же с помощью ![]() , где
, где ![]() , можно получить циклический код (7,3). Итак, если g(X) является полиномом степени
, можно получить циклический код (7,3). Итак, если g(X) является полиномом степени ![]() и множителем
и множителем ![]() , то g(X) однозначным образом генерирует циклический код (n, k).
, то g(X) однозначным образом генерирует циклический код (n, k).
6.7.3. Кодирование в систематической форме
В разделе 6.4.5 мы ввели понятие систематическая форма и рассмотрели уменьшение сложности, которое делает эту форму кодирования более привлекательной. Теперь мы хотим использовать некоторые алгебраические свойства циклического кода для развития процедуры систематического кодирования. Итак, вектор сообщения можно записать в полиномиальной форме следующим образом.
![]() (6.60)
(6.60)
В систематической форме символы сообщения используются как часть кодового слова. Мы можем сдвинуть символы сообщения в k крайних правых разряда кодового слова, а затем прибавить биты четности, разместив их в крайние левые ![]() разряды. Таким образом, осуществляется алгебраическая манипуляция полиномом сообщения, и он оказывается сдвинутым вправо на
разряды. Таким образом, осуществляется алгебраическая манипуляция полиномом сообщения, и он оказывается сдвинутым вправо на ![]() позиций. Если теперь умножить т(Х) на
позиций. Если теперь умножить т(Х) на ![]() , мы получим сдвинутый вправо полином сообщения.
, мы получим сдвинутый вправо полином сообщения.
![]() (6.61)
(6.61)
Если далее разделить уравнение (6.61) на g(X), результат можно представить в следующем виде.
![]() (6.62)
(6.62)
Здесь остаток р(Х) записывается следующим образом.
![]()
Также можно записать следующее.
![]() по модулю
по модулю ![]() (6.63)
(6.63)
Прибавляя р(Х) к обеим частям уравнения (6.62) и используя сложение по модулю 2, получаем следующее.
![]() (6.64)
(6.64)
Левая часть уравнения (6.64) является действительным полиномом кодового слова, так как это полином степени ![]() или менее, который при делении на g(X) дает нулевой остаток. Это кодовое слово можно записать через все члены полинома.
или менее, который при делении на g(X) дает нулевой остаток. Это кодовое слово можно записать через все члены полинома.
![]()
Полином кодового слова соответствует вектору кода.
![]() (6.65)
(6.65)
бит четности бит сообщения
Пример 6.8. Циклический код в систематической форме
С помощью полиномиального генератора ![]() получите систематическое кодовое слово из набора кодовых слов (7,4) для вектора сообщения m = 1 0 0 1 1.
получите систематическое кодовое слово из набора кодовых слов (7,4) для вектора сообщения m = 1 0 0 1 1.
Решение
![]()
![]()
Разделив ![]() на g(X), можно записать следующее.
на g(X), можно записать следующее.
![]()
Используя уравнение (6.64), получаем следующее.
![]()
![]()
6.7.4. Логическая схема для реализации полиномиального деления
Выше показывалось, что при циклическом сдвиге полинома кодового слова и кодировании полинома сообщения применяется операция деления полиномов друг на друга. Такие операции легко реализуются в схеме деления (регистр сдвига с обратной связью). Итак, пусть даны два полинома V(Х) и g(X), где
![]()
и
![]() ,
,
причем ![]() . Схема деления, приведенная на рис. 6.16, выполняет полиномиальное деление V(X) на g(X), определяя, таким образом, частное и остаточное слагаемое.
. Схема деления, приведенная на рис. 6.16, выполняет полиномиальное деление V(X) на g(X), определяя, таким образом, частное и остаточное слагаемое.
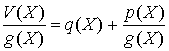
В исходном состоянии разряды регистра содержат нули. Коэффициенты V(X) поступают и продвигаются по регистру сдвига по одному за такт; начиная с коэффициентов более высокого порядка. После р-го сдвига частное на выходе равно ![]() ; это слагаемое наивысшего порядка в частном. Далее для каждого коэффициента частного
; это слагаемое наивысшего порядка в частном. Далее для каждого коэффициента частного ![]() , из делимого нужно вычитать полином
, из делимого нужно вычитать полином ![]() . Это вычитание обеспечивает обратная связь, отображенная на рис. 6.16. Разность крайних слева р слагаемых остается в делимом, а слагаемое обратной связи
. Это вычитание обеспечивает обратная связь, отображенная на рис. 6.16. Разность крайних слева р слагаемых остается в делимом, а слагаемое обратной связи ![]() формируется при каждом сдвиге схемы и отображается в виде содержимого регистра. При каждом сдвиге регистра разность смещается на один разряд; слагаемое наивысшего порядка (которое по построению схемы равно нулю) удаляется, в то время как следующий значащий коэффициент в V(Х) перемещается на его место. После всех
формируется при каждом сдвиге схемы и отображается в виде содержимого регистра. При каждом сдвиге регистра разность смещается на один разряд; слагаемое наивысшего порядка (которое по построению схемы равно нулю) удаляется, в то время как следующий значащий коэффициент в V(Х) перемещается на его место. После всех ![]() сдвигов регистра, на выход последовательно выдается частное, а остаток остается в регистре.
сдвигов регистра, на выход последовательно выдается частное, а остаток остается в регистре.
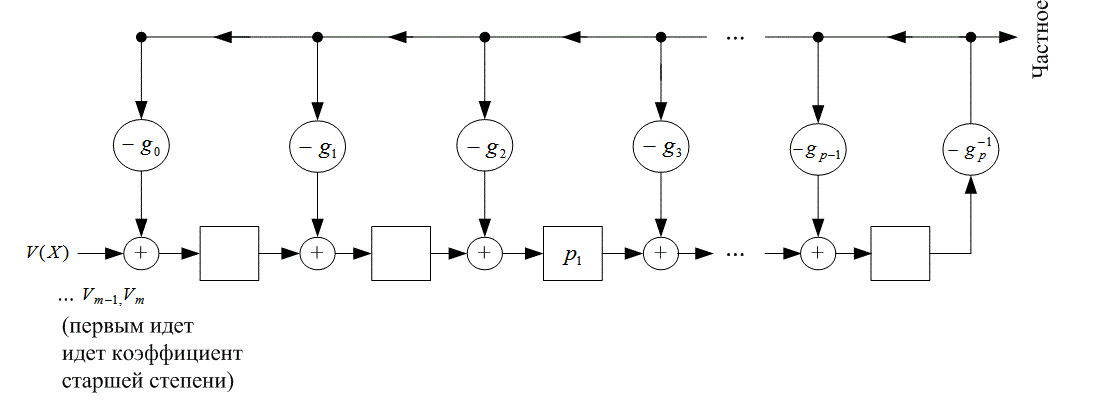
Рис.6.16. Логическая схема для реализации полиномиального деления
Пример 6.9. Схема полиномиального деления
Используя схему деления, показанную на рис. 6.16, разделите ![]()
![]() на
на ![]() ; Найдите частное и остаточное слагаемое. Сравните реализацию схемы и действия, происходящие при прямом делении полиномов.
; Найдите частное и остаточное слагаемое. Сравните реализацию схемы и действия, происходящие при прямом делении полиномов.
Решение
схема деления должна выполнить следующее действие.
![]()
необходимый регистр сдвига с обратной связью показан на рис. 6.17. Предположим, что первоначально регистр содержит нули. Схема выполнит следующие, шаги.
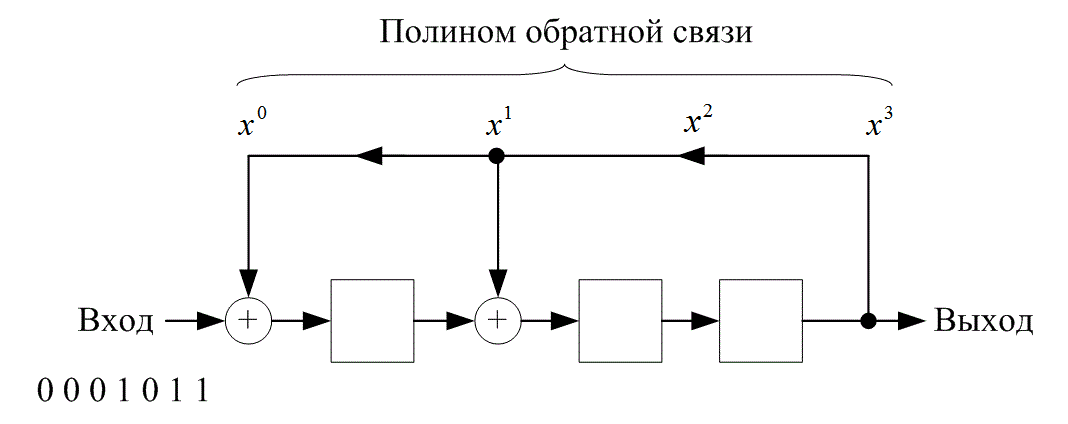
Рис. 6.17. Схема деления для примера 6.9.
Входная очередь Номер сдвига Содержимое регистра Выход и обратная связь
|
0001011 |
0 |
000 |
- |
|
000101 |
1 |
100 |
0 |
|
00010 |
2 |
110 |
0 |
|
0001 |
3 |
011 |
0 |
|
000 |
4 |
011 |
1 |
|
00 |
5 |
111 |
1 |
|
0 |
6 |
101 |
1 |
|
- |
7 |
100 |
1 |
После четвертого сдвига коэффициенты частного ![]() последовательно поступающие с выхода, выглядят как 1 1 1 1 или же полином частного имеет вид
последовательно поступающие с выхода, выглядят как 1 1 1 1 или же полином частного имеет вид ![]() . Коэффициенты остатка
. Коэффициенты остатка ![]() имеют вид 1 0 0 либо полином остатка имеет вид
имеют вид 1 0 0 либо полином остатка имеет вид ![]() . Таким образом, схема выполнила следующие вычисления.
. Таким образом, схема выполнила следующие вычисления.
![]()
Прямое деление полиномов дает результат, показанный ниже.
X6 + X5 + X3 |X3 + X + 1
обратная связь после 4-го сдвига → X6 + X4 + X3 X3+X2+X+1
обратная связь после 4-го сдвига → X5 + X4 ↑ ↑ ↑ ↑
обратная связь после 5-го сдвига → X5+ X3 + X2 4 5 6 7
регистр после 5-го сдвига → X4 + X3 + X2
обратная связь после 6-го сдвига→ X4 + X2 + X
регистр после 6-го сдвига → X3 + X
обратная связь после 7-го сдвига → X3 + X + 1
регистр после 7-го сдвига → 1
(остаток)
6.7.5. Систематическое кодирование с (n-k) - разрядным регистром сдвига
Как было показано в разделе 6.7.3, кодирование с помощью циклического кода в систематической форме включает в себя, как результат вычисления ![]() по модулю g(X), вычисление битов четности; иными словами, деление смещенного вверх (смешенного вправо) полиномиального сообщения на полиномиальный генератор g(X). Сдвиг вверх приводит к освобождению места для битов четности, которые прибавляются к разрядам сообщения, что в результате дает вектор кода в систематической форме. Сдвиг вверх на
по модулю g(X), вычисление битов четности; иными словами, деление смещенного вверх (смешенного вправо) полиномиального сообщения на полиномиальный генератор g(X). Сдвиг вверх приводит к освобождению места для битов четности, которые прибавляются к разрядам сообщения, что в результате дает вектор кода в систематической форме. Сдвиг вверх на ![]() разрядов сообщения является тривиальной операцией и в действительности не выполняется в схеме деления. На самом деле вычисляются только биты четности; затем они помещаются на соответствующие места рядом с битами сообщения. Полином четности — это остаток от деления на полиномиальный генератор; он находится в регистре n сдвигов (
разрядов сообщения является тривиальной операцией и в действительности не выполняется в схеме деления. На самом деле вычисляются только биты четности; затем они помещаются на соответствующие места рядом с битами сообщения. Полином четности — это остаток от деления на полиномиальный генератор; он находится в регистре n сдвигов (![]() )-разрядного регистра сдвига с обратной связью, показанного на рис. 6.17. Отметим, что первые n-k сдвигов по разрядам — это просто заполнение регистра. У нас не может появиться никакой обратной связи, пока не будет заполнен крайний справа разряд; следовательно, мы можем сократить цикл деления, загружая входящие данные с выхода последнего разряда, как показано на рис. 6.18. Слагаемое обратной связи в крайнем левом разряде является суммой входящих данных и крайнего правого разряда. Гарантия создания этой суммы — обеспечение
)-разрядного регистра сдвига с обратной связью, показанного на рис. 6.17. Отметим, что первые n-k сдвигов по разрядам — это просто заполнение регистра. У нас не может появиться никакой обратной связи, пока не будет заполнен крайний справа разряд; следовательно, мы можем сократить цикл деления, загружая входящие данные с выхода последнего разряда, как показано на рис. 6.18. Слагаемое обратной связи в крайнем левом разряде является суммой входящих данных и крайнего правого разряда. Гарантия создания этой суммы — обеспечение ![]() для произвольного полиномиального генератора g(X). Соединения схемы обратной связи соответствуют коэффициентам полиномиального генератора, которые записываются в следующем виде.
для произвольного полиномиального генератора g(X). Соединения схемы обратной связи соответствуют коэффициентам полиномиального генератора, которые записываются в следующем виде.
![]() (6.66)
(6.66)
Следующие шаги описывают, процедуру кодирования, использующую устройство, изображенное на рис. 6.18.
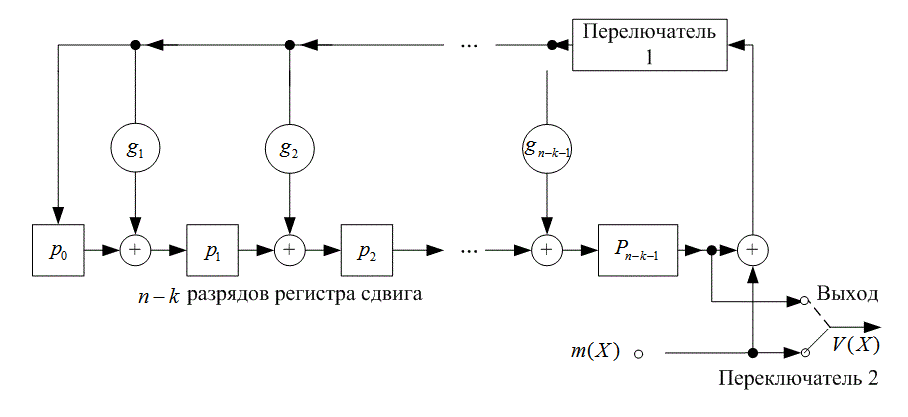
Рис. 6.18. Кодирование с помощью (п - k-разрядного регистра сдвига)
1. При первых k сдвигах ключ 1 закрыт для передачи битов сообщения в (n-k)разрядный регистр сдвига.
2. Ключ 2 установлен в нижнее положение для передачи битов сообщения на выходной регистр в течение первых k сдвигов.
3. После передачи k-го бита сообщения ключ 1 открывается, а ключ 2 переходит вверхнее положение.
4. При остальных n-k сдвигах происходит очищение кодирующих регистров, биты четности перемещаются на выходной регистр.
5. Общее число сдвигов равно n, и содержимое выходного регистра представляет собой полином кодового слова ![]() .
.
Пример 6.10. Систематическое кодирование циклического кода
Используя регистр сдвига с обратной связью, показанный на рис. 6.18, кодируйте вектор сообщения m = 1 0 1 1 в кодовое слово (7,4). Полиномиальный генератор g(X) = 1 + X + X3.
Решение
![]()
![]()
![]()
![]()
![]() по модулю
по модулю ![]()
Для ![]() -разрядного регистра сдвига, показанного на рис. 6.19, действия будут следующими.
-разрядного регистра сдвига, показанного на рис. 6.19, действия будут следующими.
Входная очередь Номер сдвига Содержание регистра Выход и обратная связь
|
1011 |
0 |
000 |
- |
|
101 |
1 |
110 |
1 |
|
10 |
2 |
101 |
1 |
|
1 |
3 |
100 |
0 |
|
- |
4 |
100 |
1 |
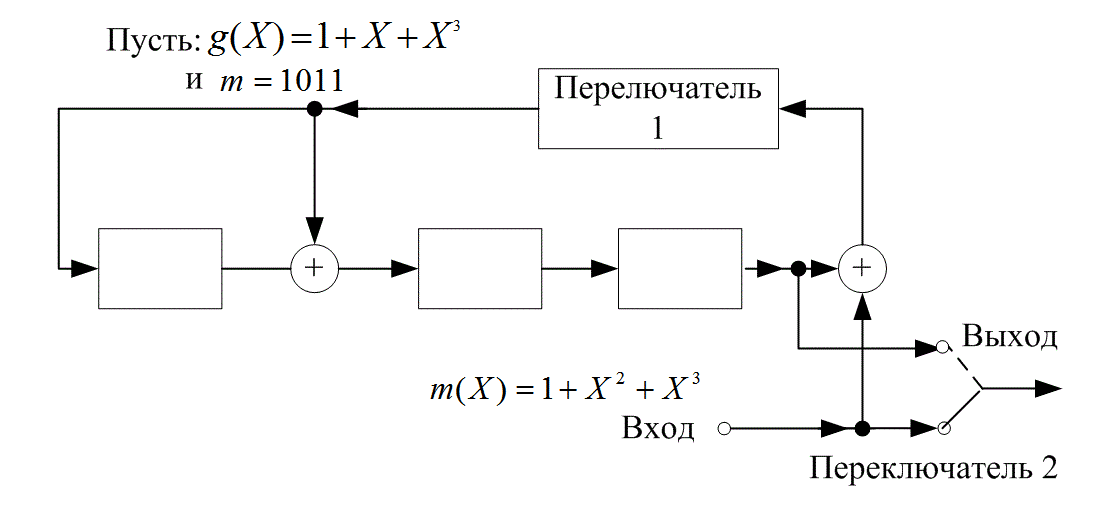
Рис. 6.19. Пример кодирования циклического кода (7, 4) с помощью (п – k)-разрядного регистра сдвига
После четвертого сдвига ключ 1 открывается, ключ 2 переходит в верхнее положение, а биты четности переходят в выходной регистр. Выходное кодовое слово U=1 0 0 1 0 1 1 или, в полиномиальной форме, U(X) = 1 + X3 + X5 + X6.
6.7.6. Обнаружение ошибок с помощью (n-k)-разрядного регистра сдвига
Передаваемое кодовое слово может быть искажено помехами, и, следовательно, принятый вектор будет искаженным вариантом переданного кодового слова. Допустим, что передается кодовое слово, имеющее в полиномиальном представлении вид U(X), a принимается вектор, в полиномиальном представлении имеющий вид Z(X). Поскольку U(X) — это полином кодового слова, он должен без остатка делиться на полиномиальный генератор g(X).
![]() (6.67)
(6.67)
Z(X), искаженную версию U(X), можно представить следующим образом.
![]() (6:68)
(6:68)
Здесь e(Х) — полином ошибочной комбинации. Декодер проверяет, является ли Z(X) полиномом кодового слова, т.е. делится ли он на g(X) без остатка. Это осуществляется путем вычисления синдрома принятого полинома. Синдром S(X) равен остатку от деления Z(X) на g(X).
![]() (6.69)
(6.69)
Здесь S(X) — полином степени ![]() или меньше. Соответственно, синдром — это
или меньше. Соответственно, синдром — это ![]() -кортеж. Используя уравнения (6.67) и (6.69), получаем следующее.
-кортеж. Используя уравнения (6.67) и (6.69), получаем следующее.
![]() (6.70)
(6.70)
Сравнивая уравнения (6.69) и (6.70), видим, что синдром S(X), полученный как Z(X) по модулю g(X), аналогичен остатку деления e(Х) на g(X). Таким образом, синдром принятого полинома Z(X) содержит информацию, необходимую для исправления ошибочной комбинации. Расчет синдрома выполняется с помощью схемы деления, почти аналогичной схеме кодирования, используемой в передатчике. Пример вычисления синдрома со сдвигом на ![]() разрядов регистра приведен на рис. 6.20 с использованием вектора кода, полученного в примере 6.10. В исходном состоянии ключ 1 закрыт, а ключ 2 открыт. Принятый вектор подается во входной регистров в котором в исходном состоянии все разряды имеют нулевое значение. После того как весь принятый вектор будет занесен в регистр сдвига, содержимое регистра — это и есть синдром. Теперь ключ 1 открывается, а ключ 2 закрывается, так что вектор синдрома теперь можно извлечь из регистра. Описанная последовательность действий имеет следующий вид.
разрядов регистра приведен на рис. 6.20 с использованием вектора кода, полученного в примере 6.10. В исходном состоянии ключ 1 закрыт, а ключ 2 открыт. Принятый вектор подается во входной регистров в котором в исходном состоянии все разряды имеют нулевое значение. После того как весь принятый вектор будет занесен в регистр сдвига, содержимое регистра — это и есть синдром. Теперь ключ 1 открывается, а ключ 2 закрывается, так что вектор синдрома теперь можно извлечь из регистра. Описанная последовательность действий имеет следующий вид.
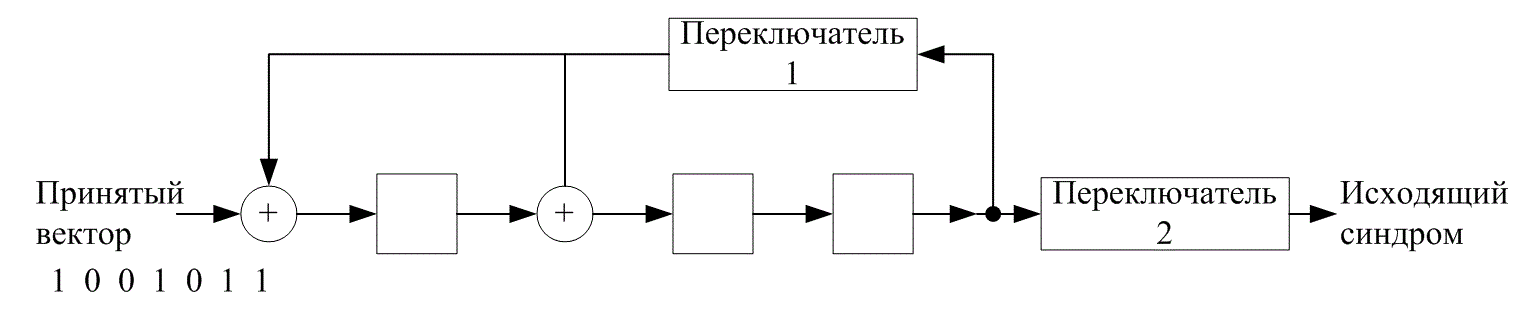
Рис. 6.20. Пример вычисления синдрома с помощью (п–k) -разрядного регистра сдвига
Входная очередь Номер сдвига Содержимое регистра
|
1001011 |
0 |
00 |
|
100101 |
1 |
100 |
|
10010 |
2 |
110 |
|
1001 |
3 |
011 |
|
100 |
4 |
011 |
|
10 |
5 |
111 |
|
1 |
6 |
101 |
|
- |
7 |
000 Синдром |
Если вектор синдрома нулевой, считается, что принятый вектор является правильным кодовым словом. Если синдром отличен от нуля, значит, обнаружена ошибка и принятый вектор — это искаженное кодовое слово; данная ошибка исправляется путем прибавления к принятому вектору вектора ошибки (указанной синдромом), т.е. аналогично процедуре, описанной в разделе 6.4.8. Этот метод декодирования хорош для простых кодов. Более сложные коды для практического использования требуют применения алгебраических методик.

