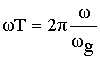Изображение по Лапласу дискретных сигналов X(p) является функцией трансцендентной, что значительно затрудняет частотный анализ дискретных сигналов. Переменную p, находящуюся в показателе экспоненты, заменяют:
X(p) заменяется на рациональную функцию, что упрощает частотный анализ.
X(Z) – Z-изображение дискретного сигнала x(nT).
Если в формулах Лапласа сделать замену:
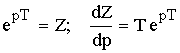
В результате получаем формулы Z-преобразования:
– прямое Z-преобразование.
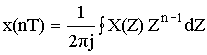– обратное Z-преобразование.
Рассмотрим особенности перехода от плоскости комплексного переменного p=σ+jω к плоскости комплексного переменного Z=x+jy.
, пусть σ=0, т.е. p=jω тогда:
где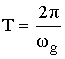 
Если ω=0, то Z=1.
Если ω=0.5ωg, то 
.
Если ω=ωg, то 
.
При увеличении переменной ω, переменная Z осуществляет многократное перемещение по единичной окружности.
По изображению X(Z) можно получить спектр дискретного сигнала, для этого вместо Z надо подставить:
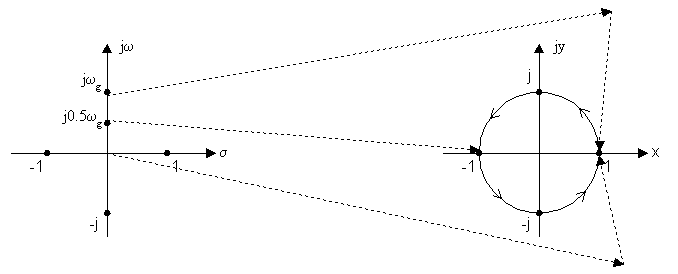
Точкам в левой полуплоскости комплексного переменного p соответствуют значения переменной внутри единичного круга на плоскости Z.
Пример 1:
Определить Z-изображение сигнала.
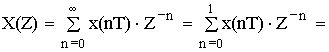
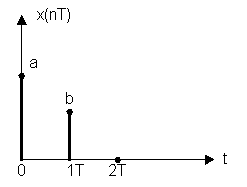
Пример 2:
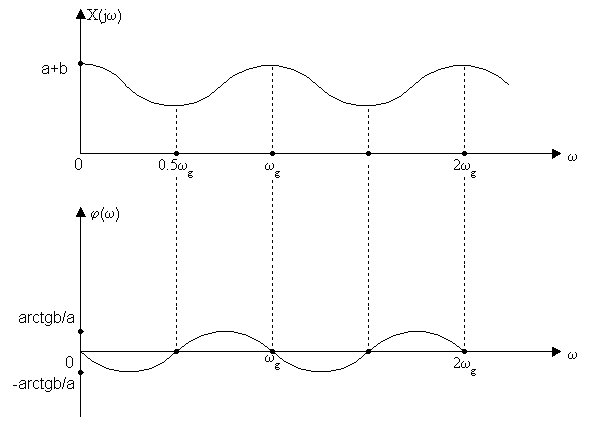
Определить спектр сигнала (пример 1).
|
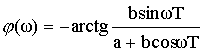
ω |
0 |
0.5ωg |
ωg |
|
|
0 |
π |
2π |
|
sinωT |
0 |
0 |
0 |
|
cosωT |
+1 |
-1 |
+1 |
|
|
a+b |
a-b |
a+b |
|
φ(ω) |
0 |
0 |
0 |
