4.5.1. Сигналы с дискретной амплитудной модуляцией

4.5.2. Сигналы с дискретной частотной модуляцией

4.5.3. Сигналы с дискретной фазовой модуляцией

Рассмотренные выше сигналы с непрерывной модуляцией, в основном используются в системах радиовещания, радиотелефонии, телевидения и других. Вместе с тем, переход на цифровые технологии в радиотехнике, в том числе и в перечисленных областях, обусловил широкое использование сигналов с дискретной модуляцией или манипуляцией. Так как исторически сигналы дискретной модуляции впервые были использованы для передачи телеграфных сообщений, такие сигналы ещё называют сигналами амплитудной (АТ), частотной (ЧТ), и фазовой (ФТ) телеграфии. Ниже при описании соответствующих сигналов будет использована эта аббревиатура, что позволит отличать их от сигналов с непрерывной модуляцией.

4.5.1. Сигналы с дискретной амплитудной модуляцией

Сигналы дискретной амплитудной модуляции характеризуются тем, что амплитуда несущего колебания изменяется в соответствии с управляющим сигналом, который представляет собой последовательности импульсов, обычно прямоугольной формы. При исследовании характеристик сигналов с непрерывной модуляцией в качестве управляющего сигнала рассматривался гармонический сигнал. По аналогии с этим для сигналов с дискретной модуляцией в качестве управляющего сигнала используем периодическую последовательность прямоугольных импульсов

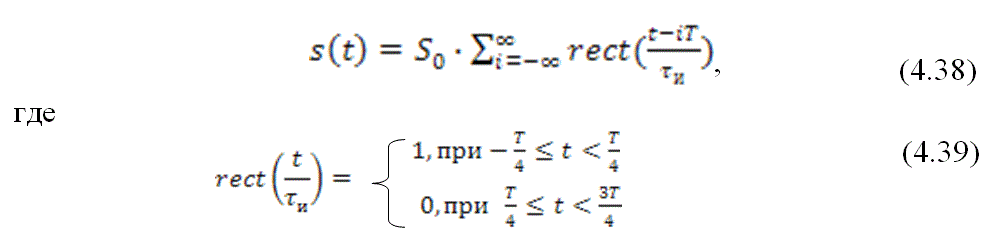
Очевидно, как следует из (4.39), длительность импульса составляет , а скважность .

На рис. 4.10 представлены эпюры управляющего сигнала , несущего колебания и амплитудно-манипулированного сигнала . Здесь и далее будем полагать амплитуду импульсов управляющего сигнала равной , а начальную фазу несущего колебания . Тогда сигнал с дискретной амплитудной модуляцией можно записать следующим образом

(4.40)

Ранее было получено разложение последовательности прямоугольных импульсов в ряд Фурье (2.13). Для рассматриваемого случая и выражение (2.13) принимает вид

, (4.41)

где .

Подставляя (4.41) в (4.40) и используя формулу произведения косинусов, получим:

. (4.42)

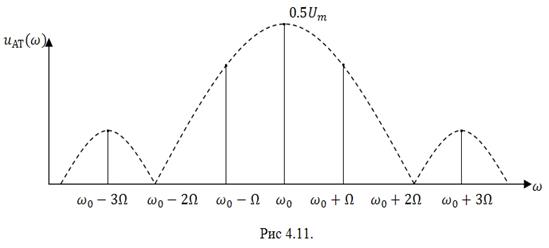
На рис. 4.11 изображён амплитудный спектр сигнала, модулированного по амплитуде последовательностью прямоугольных импульсов. Спектр содержит составляющую несущей частоты с амплитудой и две боковые полосы каждая из которых состоит из бесконечного числа гармонических составляющих, располагающихся на частотах , амплитуды которых изменяются по закону . Боковые полосы, так же как и при непрерывной АМ, расположены зеркально по отношению к спектральной составляющей несущей частоты. Нули амплитудного спектра сигнала АТ соответствуют нулям амплитудного спектра сигнала , но сдвинуты влево и вправо на величину .

Ввиду того, что основная часть энергии управляющего сигнала сосредоточена в пределах первого лепестка спектра, практическую ширину спектра в рассматриваемом случае, исходя из рис. 4.11, можно определить как

. (4.43)

Этот результат согласуется с расчётами спектра, приведёнными в [Л.4], где показано, что большая часть мощности сосредоточена в боковых составляющих с частотами и .

4.5.2. Сигналы с дискретной частотной модуляцией

При анализе сигналов с дискретной угловой модуляцией удобно в качестве модулирующего сигнала использовать периодическую последовательность прямоугольных импульсов вида “меандр”. Тогда управляющий сигнал на интервале времени принимает значение , а на интервале времени - значение . Снова, как и при анализе сигналов АТ будем полагать .

Как следует из подраздела 4.3.1 сигнал с частотной модуляцией описывается выражением (4.24). Тогда с учётом того, что на интервале управляющий сигнал , а на интервале управляющий сигнал , проведя операцию интегрирования, получим выражение сигнала ЧТ

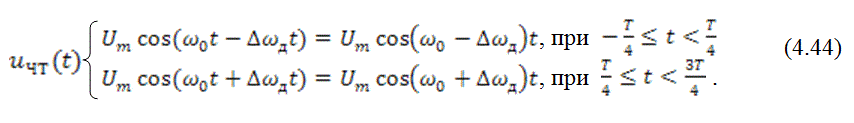
На рис 4.12 приведены временные диаграммы управляющего сигнала , несущего колебания и сигнала дискретной частотной модуляции .

С другой стороны сигнал ЧТ, как это следует из рис. 4.12, может быть представлен суммой двух сигналов дискретной амплитудной модуляции и , частоты несущих колебаний которых соответственно равны

, ,

(4.45)

а

s₁(t) = -1, при ,

s₂(t) = 1, при . (4.46)

Тогда сигнал с дискретной частотной модуляцией можно представить следующим образом

,

или с учётом (4.40)

(4.47)

Управляющие сигналы и представляют собой периодические последовательности прямоугольных импульсов одинаковой амплитуды, длительности и периода следования, но разной полярности. Тогда, в соответствии с (4.46) можно записать

;

и выражение (4.47) принимает вид:

или

, (4.48)

где описывается выражением (4.41).

Подстановка (4.41) в (4.48) после преобразований с использованием формулы произведения косинусов даёт

.

(4.49)

На рис. 4.13 изображён амплитудный спектр сигнала дискретной частотной модуляции.

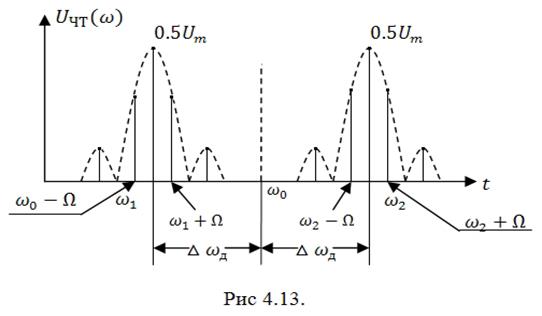
Спектр содержит две боковые полосы, расположенные симметрично относительно частоты несущего колебания. В свою очередь, каждая из боковых полос состоит из двух боковых подполос, расположенных симметрично относительно частот и . В каждой боковой подполосе располагаются спектральные составляющие на частотах и .

Очевидно, как и при непрерывной ЧМ спектр сигналов с дискретной частотной модуляцией гораздо шире спектра сигналов с дискретной амплитудной модуляцией.

Если принять во внимание, что большая часть мощности сосредоточена в боковых составляющих на частотах и , как указывалось в подразделе 4.41, то практическая ширина спектра в рассматриваемом случае равна

.

Если к тому же учесть (4.45), то можно получить

.

При практическая ширина спектра составит

,

или

.

Несмотря на значительную ширину спектра сигналы с дискретной частотной модуляцией нашли широкое применение в практической радиотехнике.

4.5.3. Сигналы с дискретной фазовой модуляцией

Выше (подраздел 4.3.1) было установлено, что сигнал с фазовой модуляцией описывается выражением

,

где - девиация фазы,

- начальная фаза колебания несущей частоты.

Если при формировании сигнала дискретной фазовой модуляции используется периодическая последовательность униполярных прямоугольных импульсов вида (4.38) и (4.39), то выражение для сигнала дискретной фазовой модуляции принимает вид

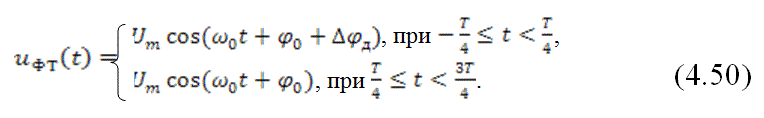
При использовании “меандра” в качестве управляющего сигнала сигнал дискретной частотной модуляции записывается следующим образом

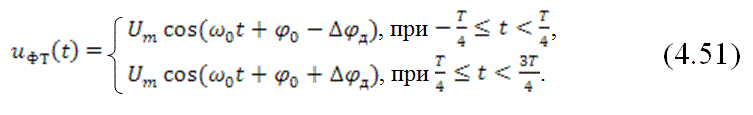
Очевидно и в том и в другом случае управляющий сигнал принимает два значения на интервале периода следования импульсов. Это означает что в сигнале дискретной фазовой модуляции на этом же интервале начальная фаза принимает два значения, которые определяются величиной . Обычно, для рассматриваемого случая эти значения отличаются на угол . Тогда для сигнала (4.50) величина , а для сигнала (4.51) величина девиации фазы составит , и выражения (4.50) и (4.51) принимают соответственно следующий вид

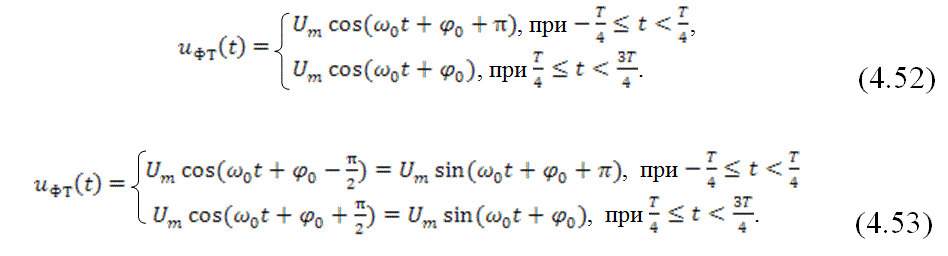
С точки зрения анализа и определения характеристик сигналов с дискретной ФМ представления (4.52) и (4.53) равноценны. Поэтому в дальнейшем мы воспользуемся представлением (4.53).

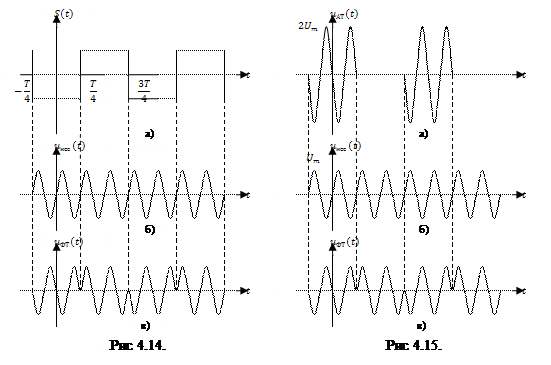
На рис. 4.14 изображены временные диаграммы управляющего сигнала , несущего колебания и сигнала с дискретной фазовой модуляцией. Здесь в соответствии с (4.53) в качестве несущего колебания выступает

. (4.54)

Найдём амплитудный спектр сигналов дискретной ФМ. Для этого представим сигнал дискретной ФМ в виде суммы несущего колебания (4.54) и сигнала дискретной амплитудной модуляции с удвоенной амплитудой и противоположной начальной фазой несущего колебания (рис. 4.15)

. (4.55)

Тогда сигнал дискретной ФМ можно записать

.

Перепишем это выражение в виде

.

Здесь использовано известное тригонометрическое соотношение

sin x = - sin (x+π).

Подставляя в это выражение разложение (4.41) управляющего сигнала, после преобразований и перестановки местами и , получим

.

C учётом того, что

,

это выражение можно привести к виду

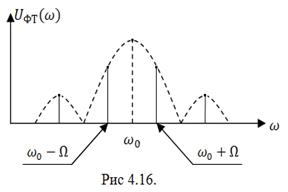
. (4.56) Соотношение (4.56) позволяет построить диаграмму амплитудного спектра сигнала дискретной ФМ, изображённую на рис. 4.16.

Из выражения (4.56) и рис. 4.16 следует, что амплитудный спектр сигналов дискретной фазовой модуляции не содержит составляющей несущего колебания, а содержит только две боковые полосы, расположенные зеркально относительно частоты . Очевидно, что в случае модуляции несущего колебания управляющим сигналом в виде периодической последовательности прямоугольных импульсов ширина спектра сигнала дискретной ФМ составляет

Δω_{фт = 2Ω .}

Сравнение (4.42) дискретной АМ с (4.56) дискретной ФМ без учёта фазовых соотношений показывает, что огибающие спектров и боковые полосы совпадают при одном и том же . Различие состоит лишь в том, что в спектре дискретной АМ составляющая несущего колебания присутствует, а в спектре дискретной ФМ нет.

Для демодуляции сигналов дискретной ФМ необходимо иметь колебание, относительно фазы которого будет измеряться фаза принимаемого сигнала дискретной ФМ. Это колебание называется опорным. В качестве опорного сигнала выступает колебание той же частоты, что и несущее колебание с амплитудой и начальной фазой

. (4.57)

Перемножим сигнал дискретной ФМ и опорный сигнал

. (4.58)

Подставляя (4.53) и (4.57) в (4.56) и используя формулу произведения синусов

,

после преобразований получим

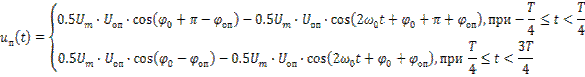
(4.57)

Результирующий сигнал содержит низкочастотную составляющую и составляющую удвоенной частоты .

Колебание удвоенной частоты может быть подавлено фильтром нижних частот. Тогда сигнал на выходе ФНЧ имеет следующий вид:

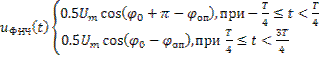
Если установить начальную фазу опорного сигнала , на выходе ФНЧ будет иметь место демодулированный сигнал

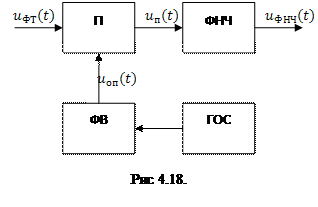
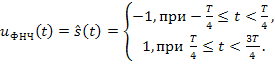
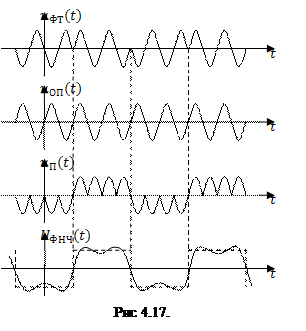
Из сказанного выше следует, что функциональная схема демодулятора сигналов дискретной ФМ должна содержать перемножитель П, генератор опорного сигнала ГОС фазовращатель ФВ и фильтр нижних частот ФНЧ. Эпюры напряжений на выходах элементов демодулятора приведены на рис. 4.17, а функциональная схема – на рис. 4.18.

В реальных радиотехнических системах опорный сигнал формируется устройством синхронизации. При этом возможны два варианта построения демодуляторов.

В первом варианте опорный сигнал формируется на передающей стороне и передаётся приёмную сторону по отдельному каналу. При этом для передачи опорного сигнала необходимы дополнительные энергетические и частотные затраты. При втором варианте опорный сигнал выделяется из информационного сигнала . В этом случае указанных дополнительных затрат не требуется, однако, техническая реализация демодулятора сложнее, чем в первом.

И в заключение отметим следующее. В подразделе 1.2 указывает что в радиотехнических системах, предназначенных для передачи цифровых сообщений, совокупность сигналов образуют ансамбль, важнейшей характеристикой которого является его объём М. Рассмотренные выше сигналы дискретной АМ, дискретной ЧМ и дискретной ФМ образуют ансамбли с М=2, т.к. управляющий сигнал может принимать только два значения. Вместе с тем, рассмотренными сигналами не ограничивается обширный класс сигналов дискретной модуляции. Дело в том, в качестве управляющих сигналов могут выступать сигналы с числом значений 4,8,…2ⁿ . Это приводит к тому, что для передачи информации используются ансамбли сигналов соответствующих объёмов. Для того чтобы отличить один ансамбль от другого не только по управляемому параметру (амплитуда, частота, начальная фаза), но и по объёму, вводится понятие кратности модуляции которая определяется как n = log₂M. Тогда рассмотренные выше сигналы являются сигналами однократной дискретной модуляции. Если М=4, то сигналы являются сигналами двукратной модуляции, при М=8 – сигналами трёхкратной модуляции и т.д. На практике широкое распространение получили сигналы многократной фазовой модуляции: двукратной (ДФТ), трёхкратной (ТФТ) и большей кратности. С вопросами формирования демодуляции таких сигналов и оценки их эффективности можно познакомиться в специальной литературе.