3.2.1. Критерий максимального правдоподобия приема сигналов
3.2.3. Реализация корреляции в согласованном фильтре
3.2.3.1. Сравнение свертки и корреляции
3.2.3.2. Дилемма в представлении упорядоченных во времени событий
3.2.4. Оптимизация вероятности ошибки
3.2.5. Вероятность возникновения ошибки при двоичной передаче сигналов
3.2.5.1. Униполярная передача сигналов
3.2.5.2. Биполярная передача сигналов
3.2.5.3. Использование базисных функций для описания передачи сигналов
3.2.1. Критерий максимального правдоподобия приема сигналов
Критерий принятия решения, используемый в этапе 2 (рис. 3.1), описывался формулой (3.7) следующим образом.
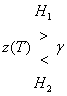
Популярный критерий выбора порога ![]() для принятия двоичного решения в выражении (3.7) основан на минимизации вероятности ошибки. Вычисление этого минимального значения ошибки
для принятия двоичного решения в выражении (3.7) основан на минимизации вероятности ошибки. Вычисление этого минимального значения ошибки ![]() начинается с записи связи отношения плотностей условных вероятностей и отношения априорных вероятностей появления сигнала. Поскольку плотность условной вероятности
начинается с записи связи отношения плотностей условных вероятностей и отношения априорных вероятностей появления сигнала. Поскольку плотность условной вероятности ![]() также называется правдоподобием
также называется правдоподобием ![]() , формулировка
, формулировка
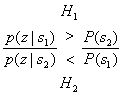 (3.31)
(3.31)
есть критерием отношения правдоподобий (см. приложение Б). В этом неравенстве ![]() и
и ![]() являются априорными вероятностями передачи сигналов
являются априорными вероятностями передачи сигналов ![]() и
и ![]() , a
, a ![]() и
и ![]() - две возможные гипотезы. Правило минимизации вероятности ошибки (формула (3.31)) гласит, что если отношение правдоподобий больше отношения априорных вероятностей, то следует выбирать гипотезу
- две возможные гипотезы. Правило минимизации вероятности ошибки (формула (3.31)) гласит, что если отношение правдоподобий больше отношения априорных вероятностей, то следует выбирать гипотезу ![]() .
.
В разделе Б.3.1 показано, что при ![]() и симметричных
и симметричных ![]()
![]() правдоподобиях подстановка формул (3.5) и (3.6) в формулу (3.31) дает
правдоподобиях подстановка формул (3.5) и (3.6) в формулу (3.31) дает
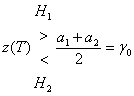 , (3.32)
, (3.32)
где ![]() - сигнальный компонент
- сигнальный компонент ![]() при передаче
при передаче ![]() , a
, a ![]() - сигнальный компонент при передаче
- сигнальный компонент при передаче ![]() . Порог
. Порог ![]() , представленный выражением
, представленный выражением ![]() , - это оптимальный порог для минимизации вероятности принятия неверного решения в этом важном частном случае. Описанный подход называется критерием минимальной ошибки.
, - это оптимальный порог для минимизации вероятности принятия неверного решения в этом важном частном случае. Описанный подход называется критерием минимальной ошибки.
Для равновероятных сигналов оптимальный порог ![]() , как показано на рис. 3.2, проходит через пересечение функций правдоподобия. Следовательно, используя формулу (3.32), видим, что этап принятия решения заключается в эффективном выборе гипотезы, соответствующей сигналу с максимальным правдоподобием. Пусть, например, значение выборки принятого сигнала равно
, как показано на рис. 3.2, проходит через пересечение функций правдоподобия. Следовательно, используя формулу (3.32), видим, что этап принятия решения заключается в эффективном выборе гипотезы, соответствующей сигналу с максимальным правдоподобием. Пусть, например, значение выборки принятого сигнала равно ![]() , а правдоподобия того, что
, а правдоподобия того, что ![]() принадлежит к одному из двух классов
принадлежит к одному из двух классов ![]() или
или ![]() , отличны от нуля. В этом случае критерий принятия решения можно рассматривать как сравнение правдоподобий
, отличны от нуля. В этом случае критерий принятия решения можно рассматривать как сравнение правдоподобий ![]() и
и ![]() . Более вероятное значение переданного сигнала соответствует наибольшей плотности вероятности. Другими словами, детектор выбирает
. Более вероятное значение переданного сигнала соответствует наибольшей плотности вероятности. Другими словами, детектор выбирает ![]() , если
, если
![]() (3.33)
(3.33)
В противном случае детектор выбирает ![]() . Детектор, минимизирующий вероятность ошибки (для классов равновероятных сигналов), называется детектором максимального правдоподобия.
. Детектор, минимизирующий вероятность ошибки (для классов равновероятных сигналов), называется детектором максимального правдоподобия.
Из рис. 3.2 можно видеть, что выражение (3.32) - это «метод здравого смысла» принятия решения при наличии статистических знаний о классах. Имея на выходе детектора значение ![]() , видим (рис. 3.2), что
, видим (рис. 3.2), что ![]() пересекается с графиком правдоподобия
пересекается с графиком правдоподобия ![]() в точке
в точке ![]() и с графиком правдоподобия
и с графиком правдоподобия ![]() в точке
в точке ![]() . Какое наиболее разумное решение должен принять детектор? В описанном случае наиболее здравым является выбор класса
. Какое наиболее разумное решение должен принять детектор? В описанном случае наиболее здравым является выбор класса ![]() , имеющего большее правдоподобие. Если бы пример был М-мерным, а не бинарным, всего существовало бы М функций правдоподобия, представляющих М классов сигналов, к которым может принадлежать принятый сигнал. Решение по принципу максимального правдоподобия в этом случае представляло бы выбор класса, имеющего самое большое правдоподобие из М возможных. (Основы теории принятия решений даются в приложении Б.)
, имеющего большее правдоподобие. Если бы пример был М-мерным, а не бинарным, всего существовало бы М функций правдоподобия, представляющих М классов сигналов, к которым может принадлежать принятый сигнал. Решение по принципу максимального правдоподобия в этом случае представляло бы выбор класса, имеющего самое большое правдоподобие из М возможных. (Основы теории принятия решений даются в приложении Б.)
3.2.1.1. Вероятность ошибки
В процессе принятия бинарного решения, показанном на рис. 3.2, существует две возможности возникновения ошибки. Ошибка ![]() появится при передаче
появится при передаче ![]() , если вследствие шума канала уровень переданного сигнала
, если вследствие шума канала уровень переданного сигнала ![]() упадет ниже
упадет ниже ![]() . Вероятность этого равна следующему.
. Вероятность этого равна следующему.
![]() (3.34)
(3.34)
Эта возможность показана заштрихованной областью слева от ![]() (рис. 3.2). Подобным образом ошибка появляется при передаче
(рис. 3.2). Подобным образом ошибка появляется при передаче ![]() , если вследствие шума канала уровень переданного сигнала
, если вследствие шума канала уровень переданного сигнала ![]() поднимется выше
поднимется выше ![]() . Вероятность этого равна следующему.
. Вероятность этого равна следующему.
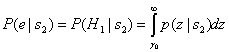 (3.35)
(3.35)
Суммарная вероятность ошибки равна сумме вероятностей всех возможностей ее появления. Для бинарного случая вероятность возникновения ошибочного бита можно выразить следующим образом.
![]() (3.36)
(3.36)
Объединяя формулы (3.34)-(3.36), получаем
![]() (3.37,а)
(3.37,а)
или, что равносильно,
![]() (3.37,б)
(3.37,б)
Иными словами, при передаче сигнала ![]() ошибка происходит при выборе гипотезы
ошибка происходит при выборе гипотезы ![]() ; или при передаче сигнала
; или при передаче сигнала ![]() ошибка происходит при выборе гипотезы
ошибка происходит при выборе гипотезы ![]() . Для равных априорных вероятностей (т.е.
. Для равных априорных вероятностей (т.е. ![]() ) имеем следующее.
) имеем следующее.
![]() (3.38)
(3.38)
Используя симметричность плотностей вероятности, получаем следующее.
![]() (3.39)
(3.39)
Вероятность появления ошибочного бита, ![]() , численно равна площади под «хвостом» любой функции правдоподобия,
, численно равна площади под «хвостом» любой функции правдоподобия, ![]() или
или ![]() , «заползающим» на «неправильную» сторону порога. Таким образом, для вычисления
, «заползающим» на «неправильную» сторону порога. Таким образом, для вычисления ![]() мы можем проинтегрировать
мы можем проинтегрировать
![]() от
от ![]() до
до ![]() или
или ![]() - от
- от ![]() до
до ![]() .
.
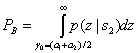 (3.40)
(3.40)
Здесь ![]() - оптимальный порог из уравнения (3.32). Заменяя правдоподобие
- оптимальный порог из уравнения (3.32). Заменяя правдоподобие ![]() его гауссовым эквивалентом из формулы (3.6), имеем
его гауссовым эквивалентом из формулы (3.6), имеем
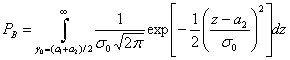 (3.41)
(3.41)
где ![]() - дисперсия шума вне коррелятора.
- дисперсия шума вне коррелятора.
Сделаем замену ![]() . Тогда
. Тогда ![]() и
и
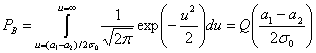 (3.42)
(3.42)
Здесь ![]() называется гауссовым интегралом ошибок и часто используется при описании вероятности с гауссовой плотностью распределения. Определяется эта функция следующим образом.
называется гауссовым интегралом ошибок и часто используется при описании вероятности с гауссовой плотностью распределения. Определяется эта функция следующим образом.
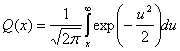 (3.43)
(3.43)
Отметим, что гауссов интеграл ошибок может определяться несколькими способами (см. приложение Б); впрочем, все определения одинаково пригодны для описания вероятности ошибки при гауссовом шуме. ![]() нельзя вычислить в аналитическом виде. В табл. Б.1 она представлена в форме таблицы. Хорошие аппроксимации функции
нельзя вычислить в аналитическом виде. В табл. Б.1 она представлена в форме таблицы. Хорошие аппроксимации функции ![]() через более простые функции можно найти в работе [5]. Вот одна из таких аппроксимаций, справедливая для
через более простые функции можно найти в работе [5]. Вот одна из таких аппроксимаций, справедливая для ![]() .
.
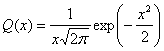 (3.44)
(3.44)
Итак, мы оптимизировали (в смысле минимизации ![]() ) порог
) порог ![]() , но не оптимизировали принимающий фильтр в блоке 1 (рис. 3.1). Далее нашей целью является оптимизация этого фильтра путем максимизации аргумента
, но не оптимизировали принимающий фильтр в блоке 1 (рис. 3.1). Далее нашей целью является оптимизация этого фильтра путем максимизации аргумента ![]() в формуле (3.42).
в формуле (3.42).
3.2.2. Согласованный фильтр
Согласованный фильтр (matched filter) - это линейное устройство, спроектированное, чтобы давать на выходе максимально возможное для данного передаваемого сигнала отношение сигнал/шум. Предположим, что на вход линейного, инвариантного относительно времени (принимающего) фильтра, за которым следует устройство дискретизации (рис. 3.1), подается известный сигнал ![]() плюс шум AWGN
плюс шум AWGN ![]() . В момент времени
. В момент времени ![]() сигнал на выходе устройства дискретизации
сигнал на выходе устройства дискретизации ![]() состоит из компонента сигнала
состоит из компонента сигнала ![]() , и компонента шума
, и компонента шума ![]() . Дисперсия шума на выходе (средняя мощность шума) записывается как
. Дисперсия шума на выходе (средняя мощность шума) записывается как ![]() , так что отношение мгновенной мощности шума к средней мощности шума,
, так что отношение мгновенной мощности шума к средней мощности шума, ![]() , в момент
, в момент ![]() вне устройства дискретизации на этапе 1 равно следующему.
вне устройства дискретизации на этапе 1 равно следующему.
![]() (3.45)
(3.45)
Нам нужно найти передаточную функцию фильтра ![]() с максимальным отношением
с максимальным отношением ![]() . Сигнал
. Сигнал ![]() на выходе фильтра можно выразить через передаточную функцию фильтра
на выходе фильтра можно выразить через передаточную функцию фильтра ![]() (до оптимизации) и Фурье-образ сигнала на входе
(до оптимизации) и Фурье-образ сигнала на входе
![]() , (3.46)
, (3.46)
где ![]() - Фурье-образ сигнала на входе,
- Фурье-образ сигнала на входе, ![]() . Если двусторонняя спектральная плотность мощности шума на входе равна
. Если двусторонняя спектральная плотность мощности шума на входе равна ![]() Вт/Гц, то с помощью формул (1.19) и (1.53) мощность шума на выходе можно записать следующим образом.
Вт/Гц, то с помощью формул (1.19) и (1.53) мощность шума на выходе можно записать следующим образом.
![]() (3.47)
(3.47)
Объединяя формулы (3.45) и (3.47), получаем выражение для ![]() .
.
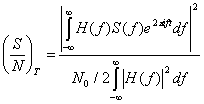 (3.48)
(3.48)
Найдем теперь значение ![]() , при котором
, при котором ![]() достигает максимума. Для этого нам понадобится неравенство Шварца, одна из форм записи которого представлена ниже.
достигает максимума. Для этого нам понадобится неравенство Шварца, одна из форм записи которого представлена ниже.
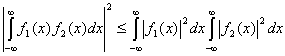 (3.49)
(3.49)
Равенство достигается при ![]() , где
, где ![]() - произвольная константа, а знак «*» обозначает комплексно сопряженное значение. Если отождествить
- произвольная константа, а знак «*» обозначает комплексно сопряженное значение. Если отождествить ![]() с
с ![]() и
и ![]() с
с ![]() , можем записать следующее.
, можем записать следующее.
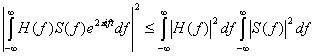 (3.50)
(3.50)
Подстановка в выражение (3.48) дает
![]() (3.51)
(3.51)
или
![]() , (3.52)
, (3.52)
где энергия Е входящего сигнала ![]() равна следующему.
равна следующему.
![]() (3.53)
(3.53)
Следовательно, максимальный выход ![]() зависит от энергии входящего сигнала и спектральной плотности мощности шума, но не от конкретной формы сигнала.
зависит от энергии входящего сигнала и спектральной плотности мощности шума, но не от конкретной формы сигнала.
Равенство в выражении (3.52) получается только при использовании оптимальной передаточной функции фильтра ![]() .
.
![]() (3.54)
(3.54)
или
![]() (3.55)
(3.55)
Поскольку ![]() - вещественный сигнал, с помощью формул (А.29) и (А.31) можно записать следующее.
- вещественный сигнал, с помощью формул (А.29) и (А.31) можно записать следующее.
![]()
![]()
![]()
![]() (3.56)
(3.56)
Итак, импульсная характеристика фильтра, дающего максимальное отношение сигнал/шум на выходе, является зеркальным отображением сигнала сообщения ![]() , запаздывающим на время передачи символа Т. Отметим, что задержка в Т секунд делает уравнение (3.56) причинным, т.е. запаздывание на Т секунд делает
, запаздывающим на время передачи символа Т. Отметим, что задержка в Т секунд делает уравнение (3.56) причинным, т.е. запаздывание на Т секунд делает ![]() функцией положительного времени в промежутке
функцией положительного времени в промежутке ![]() , Без задержки в Т секунд отклик
, Без задержки в Т секунд отклик ![]() нереализуем, поскольку в этом случае он является функцией отрицательного времени.
нереализуем, поскольку в этом случае он является функцией отрицательного времени.
3.2.3. Реализация корреляции в согласованном фильтре
В формуле (3.56) и на рис. 3.7, а отражено основное свойство согласованного фильтра: импульсная характеристика такого фильтра - это зеркальное отображение сигнала с некоторой задержкой (относительно оси ![]() ). Следовательно, если сигнал равен
). Следовательно, если сигнал равен ![]() , его зеркальное отображение равно
, его зеркальное отображение равно ![]() , а зеркальное отображение, запаздывающее на Т секунд, - это
, а зеркальное отображение, запаздывающее на Т секунд, - это ![]() . Выход
. Выход ![]() причинного фильтра во временной области можно описать как свертку принятого входного сигнала
причинного фильтра во временной области можно описать как свертку принятого входного сигнала ![]() с импульсной характеристикой фильтра (см. раздел А.5).
с импульсной характеристикой фильтра (см. раздел А.5).
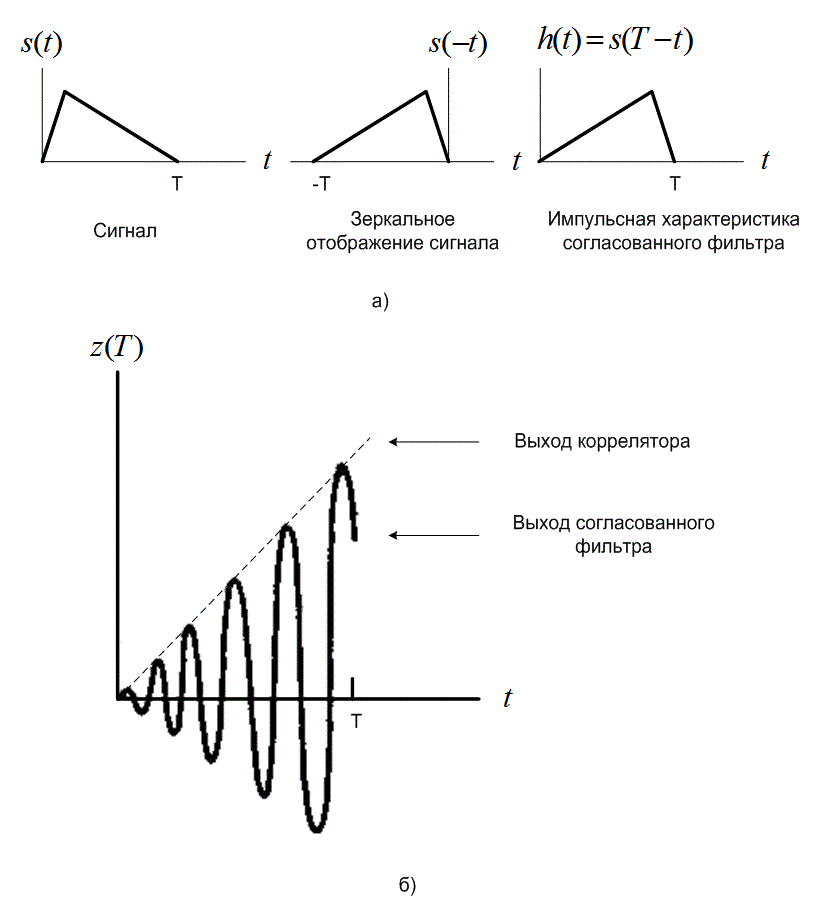
Рис.3.7. Коррелятор и согласованный фильтр: а) характеристика согласованного фильтра; б) сравнение выходов коррелятора и согласованного фильтра
Подставляя ![]() из формулы (3.56) в
из формулы (3.56) в ![]() в формуле (3.57) и выбирая произвольную константу
в формуле (3.57) и выбирая произвольную константу ![]() равной единице, получаем следующее.
равной единице, получаем следующее.
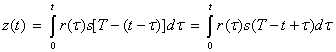 (3.58)
(3.58)
Для момента времени ![]() формулу (3.58) можно переписать следующим образом.
формулу (3.58) можно переписать следующим образом.
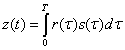 (3.59)
(3.59)
Из последнего выражения видно, что интеграл от произведения принятого сигнала ![]() на копию переданного сигнала
на копию переданного сигнала ![]() на интервале передачи символа представляет собой корреляцию
на интервале передачи символа представляет собой корреляцию ![]() с
с ![]() . Предположим, что принятый сигнал
. Предположим, что принятый сигнал ![]() коррелирует со всеми Сигналами-прототипами
коррелирует со всеми Сигналами-прототипами ![]()
![]() и для этого используется набор из М корреляторов. Сигнал
и для этого используется набор из М корреляторов. Сигнал ![]() , корреляция которого (или интеграл от произведения) с
, корреляция которого (или интеграл от произведения) с ![]() дает максимальное значение
дает максимальное значение ![]() , - и есть сигнал, который согласуется с
, - и есть сигнал, который согласуется с ![]() лучше остальных. Далее это свойство корреляции мы будем использовать для оптимального обнаружения сигналов.
лучше остальных. Далее это свойство корреляции мы будем использовать для оптимального обнаружения сигналов.
3.2.3.1. Сравнение свертки и корреляции
Работа согласованного фильтра описывается математической операцией свертки; сигнал сворачивается с импульсной характеристикой фильтра. Работа коррелятора описывается математической операцией корреляции; сигнал коррелирует с копией самого себя. Довольно часто термин «согласованный фильтр» используется как синоним термина «коррелятор». Как такое возможно, если математические операции различны? Напомним, что процесс свертки двух сигналов использует один из сигналов, обращенный во времени. Кроме того, импульсная характеристика согласованного фильтра определяется именно через сигнал, обращенный во времени. Следовательно, свертка в согласованном фильтре с обращенной во времени функцией дает еще одно обращение во времени, подавая на выход (в конце интервала передачи символа) то, что является корреляцией сигнала с собственной копией. Значит, принимающий фильтр, изображенный на рис. 3.1, можно реализовать либо как согласованный фильтр, либо как коррелятор. Важно отметить, что выходы коррелятора и согласованного фильтра одинаковы только в момент времени ![]() . Для синусоидального входа выход коррелятора,
. Для синусоидального входа выход коррелятора, ![]() , на промежутке
, на промежутке ![]() приблизительно описывается линейной функцией. В то же время выход согласованного фильтра приблизительно описывается синусоидой, амплитуда которой в том же промежутке времени модулирована линейной функцией (см. рис. 3.7, б). Поскольку при соизмеримых входах выходы согласованного фильтра и коррелятора идентичны в момент взятия выборки
приблизительно описывается линейной функцией. В то же время выход согласованного фильтра приблизительно описывается синусоидой, амплитуда которой в том же промежутке времени модулирована линейной функцией (см. рис. 3.7, б). Поскольку при соизмеримых входах выходы согласованного фильтра и коррелятора идентичны в момент взятия выборки ![]() , функции согласованного фильтра и коррелятора, изображенные на рис. 3.8, часто используются как взаимозаменяемые.
, функции согласованного фильтра и коррелятора, изображенные на рис. 3.8, часто используются как взаимозаменяемые.
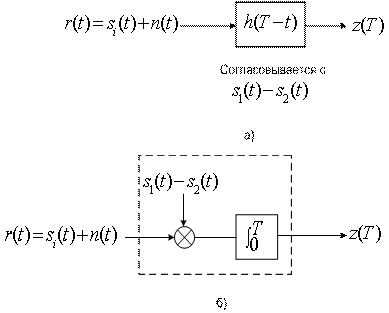
Рис.3.8. Эквивалентность согласованного фильтра и коррелятора:
а) согласованный фильтр; б) коррелятор
3.2.3.2. Дилемма в представлении упорядоченных во времени событий
При представлении упорядоченных во времени событий существует серьезная проблема. Возникает частая ошибка в области электротехники - путаница между самым старшим битом и самым младшим. На рис. 3.9, а показано, как обычно изображается функция времени; самое раннее событие представлено слева, а наиболее позднее - справа. Людям, привыкшим читать слева направо, такое изображение кажется единственно правильным. Рассмотрим рис. 3.9, б, где показано, как импульсы поступают в сеть (или канал) и покидают ее. Здесь самое раннее событие изображено справа, а наиболее позднее - слева. Изучение этого рисунка позволяет понять, что при записи упорядоченных событий возможна путаница между двумя возможными форматами записи. Чтобы избежать затруднений, зачастую необходимо дать некоторые пояснения (например, указать, что крайний справа бит - это первый бит).
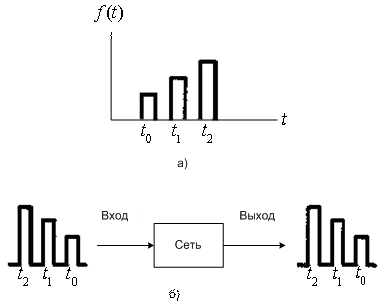
Рис.3.9. Дилемма в представлении упорядоченных во времени событий
Математические соотношения часто имеют «врожденные» особенности, гарантирующие соответствующее упорядочение событий. Например, в разделе 3.2.3 согласованный фильтр определялся как имеющий импульсную характеристику ![]() - запаздывающую версию обращенной во времени копии сигнала. Иными словами,
- запаздывающую версию обращенной во времени копии сигнала. Иными словами, ![]() . Запаздывание на один интервал передачи символа Т необходимо для того, чтобы фильтр был причинным (выход должен быть функцией положительного времени). Обращение во времени можно рассматривать как «предварительную коррекцию», где крайняя правая часть временного графика теперь соответствует наиболее раннему событию. Поскольку свертка навязывает другое обращение во времени, поступающий сигнал и импульсный отклик фильтра будут «идти в ногу» (ранний с ранним, поздний с поздним).
. Запаздывание на один интервал передачи символа Т необходимо для того, чтобы фильтр был причинным (выход должен быть функцией положительного времени). Обращение во времени можно рассматривать как «предварительную коррекцию», где крайняя правая часть временного графика теперь соответствует наиболее раннему событию. Поскольку свертка навязывает другое обращение во времени, поступающий сигнал и импульсный отклик фильтра будут «идти в ногу» (ранний с ранним, поздний с поздним).
3.2.4. Оптимизация вероятности ошибки
Для оптимизации (минимизации) ![]() в среде канала и приемника с шумом AWGN, показанных на рис. 3.1, нужно выбрать оптимальный принимающий фильтр на этапе 1 и оптимальный порог принятия решения на этапе 2. Для двоичного случая оптимальный порог принятия решения уже выбран и дается формулой (3.32), а в формуле (3.42) показано, что вероятность ошибки при таком пороге равна
в среде канала и приемника с шумом AWGN, показанных на рис. 3.1, нужно выбрать оптимальный принимающий фильтр на этапе 1 и оптимальный порог принятия решения на этапе 2. Для двоичного случая оптимальный порог принятия решения уже выбран и дается формулой (3.32), а в формуле (3.42) показано, что вероятность ошибки при таком пороге равна ![]() . Для минимального
. Для минимального ![]() в общем случае необходимо выбрать фильтр (согласованный) с максимальным аргументом функции
в общем случае необходимо выбрать фильтр (согласованный) с максимальным аргументом функции ![]() . Следовательно, нужно определить максимальное
. Следовательно, нужно определить максимальное ![]() , что равносильно максимальному
, что равносильно максимальному
![]() , (3.60)
, (3.60)
где ![]() - разность желательных компонентов сигнала на выходе фильтра в момент
- разность желательных компонентов сигнала на выходе фильтра в момент ![]() , а квадрат этого разностного сигнала представляет его мгновенную мощность. В разделе 3.2.2 описывался согласованный фильтр с максимальным отношением сигнал/шум (signal-to-noise ratio - SNR) для данного известного сигнала. Здесь мы решаем вопрос двоичной передачи сигналов и ищем оптимальный фильтр с максимальной разностью двух возможных выходных сигналов. В выводе, приведенном в уравнениях (3.45)-(3.52), было показано, что согласованный фильтр дает на выходе максимально возможное отношение SNR, равное
, а квадрат этого разностного сигнала представляет его мгновенную мощность. В разделе 3.2.2 описывался согласованный фильтр с максимальным отношением сигнал/шум (signal-to-noise ratio - SNR) для данного известного сигнала. Здесь мы решаем вопрос двоичной передачи сигналов и ищем оптимальный фильтр с максимальной разностью двух возможных выходных сигналов. В выводе, приведенном в уравнениях (3.45)-(3.52), было показано, что согласованный фильтр дает на выходе максимально возможное отношение SNR, равное ![]() . Допустим, что фильтр согласовывает входящий разностный сигнал
. Допустим, что фильтр согласовывает входящий разностный сигнал ![]() . Следовательно, в момент
. Следовательно, в момент ![]() можем записать отношение SNR на выходе.
можем записать отношение SNR на выходе.
![]() , (3.61)
, (3.61)
где ![]() - двусторонняя спектральная плотность мощности шума на входе фильтра и
- двусторонняя спектральная плотность мощности шума на входе фильтра и
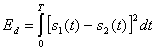 (3.62)
(3.62)
является энергией разностного сигнала на входе фильтра. Отметим, что уравнение (3.61) не представляет отношения SNR для какой-то отдельной передачи, ![]() или
или ![]() . Это отношение дает метрику разности сигналов на выходе фильтра. Максимизируя выходное отношение SNR, как показано в уравнении (3.61), согласованный фильтр обеспечивает максимальное расстояние (нормированное на шум) между двумя возможными выходами – сигналами
. Это отношение дает метрику разности сигналов на выходе фильтра. Максимизируя выходное отношение SNR, как показано в уравнении (3.61), согласованный фильтр обеспечивает максимальное расстояние (нормированное на шум) между двумя возможными выходами – сигналами ![]() и
и ![]() .
.
Далее, объединяя уравнения (3.42) и (3.61), получаем следующее.
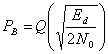 (3.63)
(3.63)
Для согласованного фильтра уравнение (3.63) является важным промежуточным результатом, включающим энергию разностного сигнала на входе фильтра. Из этого уравнения можно вывести более общее соотношение для энергии принятого бита. Для начала определим временной коэффициент взаимной корреляции ![]() , который будем использовать в качестве меры подобия двух сигналов
, который будем использовать в качестве меры подобия двух сигналов ![]() и
и ![]() . Имеем
. Имеем
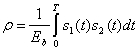 (3.64,а)
(3.64,а)
и
![]() (3.64,б)
(3.64,б)
где ![]() . Формула (3.64,а) - это классический математический способ выражения корреляции. Впрочем, если рассматривать
. Формула (3.64,а) - это классический математический способ выражения корреляции. Впрочем, если рассматривать ![]() и
и ![]() как векторы сигналов
как векторы сигналов ![]() и
и ![]() , то более удобным представлением
, то более удобным представлением ![]() является формула (3.64,6). Векторное представление позволяет получать удобные графические изображения. Векторы
является формула (3.64,6). Векторное представление позволяет получать удобные графические изображения. Векторы ![]() и
и ![]() разделены углом
разделены углом ![]() ; при малом угле векторы достаточно подобны (сильно коррелируют), а при больших углах они отличаются. Косинус угла
; при малом угле векторы достаточно подобны (сильно коррелируют), а при больших углах они отличаются. Косинус угла ![]() дает ту же нормированную метрику корреляции, что и формула (3.64,а).
дает ту же нормированную метрику корреляции, что и формула (3.64,а).
Расписывая выражение (3.62), получаем следующее.
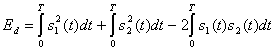 (3.65)
(3.65)
Напомним, что два первых члена формулы (3.65) представляют энергию, связанную с битом, ![]() .
.
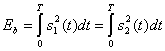 (3.66)
(3.66)
Подставляя уравнения (3.64,а) и (3.66) в формулу (3.65), получаем следующее.
![]() (3.67)
(3.67)
Подставляя уравнение (3.67) в (3.63), получаем следующее.
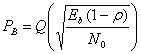 (3.68)
(3.68)
Рассмотрим случай ![]() , соответствующий наилучшей корреляции сигналов
, соответствующий наилучшей корреляции сигналов ![]() и
и ![]() в течение времени передачи символа (если сигналы изобразить как векторы, угол между ними будет равен нулю). Возможно ли, чтобы подобные сигналы использовались кем-то в реальной системе? Разумеется, нет, поскольку сигналы связи (элементы алфавита) должны быль максимально несопоставимы, чтобы их можно было легко различать (обнаруживать). В данный момент мы просто рассматриваем возможные значения
в течение времени передачи символа (если сигналы изобразить как векторы, угол между ними будет равен нулю). Возможно ли, чтобы подобные сигналы использовались кем-то в реальной системе? Разумеется, нет, поскольку сигналы связи (элементы алфавита) должны быль максимально несопоставимы, чтобы их можно было легко различать (обнаруживать). В данный момент мы просто рассматриваем возможные значения ![]() . Следующий частный случай
. Следующий частный случай ![]() соответствует «антикорреляции»
соответствует «антикорреляции» ![]() и
и ![]() в течение времени передачи символа. Другими словами, угол между векторами сигналов составляет 180°. В этом случае, когда векторы являются зеркальными отображениями друг друга, как показано на рис. 3.10, а, сигналы называются антиподными. Рассмотрим также случай
в течение времени передачи символа. Другими словами, угол между векторами сигналов составляет 180°. В этом случае, когда векторы являются зеркальными отображениями друг друга, как показано на рис. 3.10, а, сигналы называются антиподными. Рассмотрим также случай ![]() , соответствующий нулевой корреляции между
, соответствующий нулевой корреляции между ![]() и
и ![]() (угол между векторами равен 90°). Такие сигналы, показанные на рис. 3.10, б, именуются ортогональными. Чтобы два сигнала были ортогональными, они не должны коррелировать в течение времени передачи символа, т.е. должно выполняться следующее условие.
(угол между векторами равен 90°). Такие сигналы, показанные на рис. 3.10, б, именуются ортогональными. Чтобы два сигнала были ортогональными, они не должны коррелировать в течение времени передачи символа, т.е. должно выполняться следующее условие.
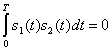 (3.69)
(3.69)
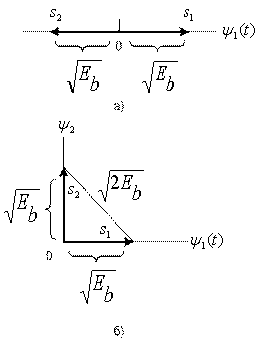
Рис. 3.10. Векторы двоичных сигналов: а) антиподные; б) ортогональные
Вопрос ортогональности рассматривался ранее, в разделе 3.1.3. При обнаружении антиподных сигналов (т.е. при ![]() ) с помощью согласованного фильтра, уравнение (3.68) можно записать следующим образом.
) с помощью согласованного фильтра, уравнение (3.68) можно записать следующим образом.
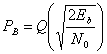 (3.70)
(3.70)
Точно так же при обнаружении ортогональных сигналов (т.е. при ![]() ) с помощью согласованного фильтра, формулу (3.68) можно записать следующим образом.
) с помощью согласованного фильтра, формулу (3.68) можно записать следующим образом.
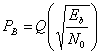 (3.71)
(3.71)
На рис. 3.10, где амплитуды сигналов выбраны равными ![]() , показано, что вероятность ошибки, описываемая уравнениями (3.70) и (3.71), является функцией расстояния между
, показано, что вероятность ошибки, описываемая уравнениями (3.70) и (3.71), является функцией расстояния между ![]() и
и ![]() (чем больше расстояние, тем меньше
(чем больше расстояние, тем меньше ![]() ). Если взять антиподные сигналы (рис. 3.10, а), расстояние между ними будет равно
). Если взять антиподные сигналы (рис. 3.10, а), расстояние между ними будет равно ![]() , а энергия
, а энергия ![]() , связанная с расстоянием, будет выражаться как квадрат расстояния, или
, связанная с расстоянием, будет выражаться как квадрат расстояния, или ![]() . При подстановке
. При подстановке ![]() в уравнение (3.63) получаем уравнение (3.70). Если взять ортогональные сигналы (рис. 3.10, б), расстояние между ними будет равно
в уравнение (3.63) получаем уравнение (3.70). Если взять ортогональные сигналы (рис. 3.10, б), расстояние между ними будет равно ![]() ; следовательно,
; следовательно, ![]() . При подстановке
. При подстановке ![]() в уравнение (3.63) получим уравнение (3.71).
в уравнение (3.63) получим уравнение (3.71).
Пример 3.2. Обнаружение антиподных сигналов с помощью согласованного фильтра
Рассмотрим бинарную систему связи, принимающую равновероятные сигналы ![]() и
и ![]() плюс шум AWGN (рис. 3.11). Предположим, что в качестве принимающего фильтра используется согласованный фильтр и спектральная плотность мощности шума
плюс шум AWGN (рис. 3.11). Предположим, что в качестве принимающего фильтра используется согласованный фильтр и спектральная плотность мощности шума ![]() равна
равна ![]() Вт/Гц. С помощью значения напряжения и времени принятого сигнала, показанных на рис. 3.11, вычислите вероятность появления ошибочного бита.
Вт/Гц. С помощью значения напряжения и времени принятого сигнала, показанных на рис. 3.11, вычислите вероятность появления ошибочного бита.
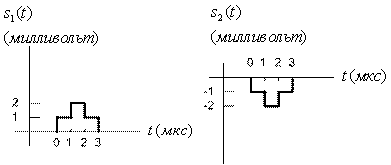
Рис.3.11. Узкополосные аналоговые сигналы
Решение
Мы можем графически определить отношение принятой энергии на бит сигнала, используя для этого один из двух графиков, либо ![]() , либо
, либо ![]() , представленных на рис. 3.11. Энергия - это площадь под графиком импульса, которая находится путем интегрирования.
, представленных на рис. 3.11. Энергия - это площадь под графиком импульса, которая находится путем интегрирования.
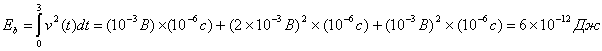
Поскольку сигналы, изображенные на рис. 3.11, являются антиподными и обнаруживаются с помощью согласованного фильтра, используем формулу (3.70) для вычисления вероятности появления ошибочного бита.
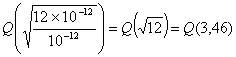
Из табл. Б.1 находим, что ![]() . Кроме того, поскольку аргумент
. Кроме того, поскольку аргумент ![]() больше 3, можно также использовать приближенное соотношение, приведенное в формуле (3.44), которое дает вероятность
больше 3, можно также использовать приближенное соотношение, приведенное в формуле (3.44), которое дает вероятность ![]() . Поскольку принятые сигналы являются антиподными и принимаются согласованным фильтром, весьма вероятно, что формула (3.70) дает верное выражение для нахождения вероятности возникновения ошибочного бита. Сигналы
. Поскольку принятые сигналы являются антиподными и принимаются согласованным фильтром, весьма вероятно, что формула (3.70) дает верное выражение для нахождения вероятности возникновения ошибочного бита. Сигналы ![]() и
и ![]() могут выглядеть гораздо более странно, но до тех пор, пока они являются антиподными и обнаруживаются с помощью согласованного фильтра, их внешний вид не влияет на вычисление
могут выглядеть гораздо более странно, но до тех пор, пока они являются антиподными и обнаруживаются с помощью согласованного фильтра, их внешний вид не влияет на вычисление ![]() . Формы сигналов, разумеется, имеют значение, но только когда дело доходит до определения импульсного отклика согласованного фильтра, необходимого для обнаружения этих сигналов.
. Формы сигналов, разумеется, имеют значение, но только когда дело доходит до определения импульсного отклика согласованного фильтра, необходимого для обнаружения этих сигналов.
3.2.5. Вероятность возникновения ошибки при двоичной передаче сигналов
3.2.5.1. Униполярная передача сигналов
На рис. 3.12, а приведен пример узкополосной ортогональной передачи сигналов, называемой униполярной.
![]()
![]()
![]()
![]()
![]() (3.72)
(3.72)
Здесь ![]() - амплитуда сигнала
- амплитуда сигнала ![]() . Определение ортогональной передачи сигналов дается выражением (3.69), требующим, чтобы
. Определение ортогональной передачи сигналов дается выражением (3.69), требующим, чтобы ![]() и
и ![]() имели нулевую корреляцию в течение периода передачи символа.
имели нулевую корреляцию в течение периода передачи символа.
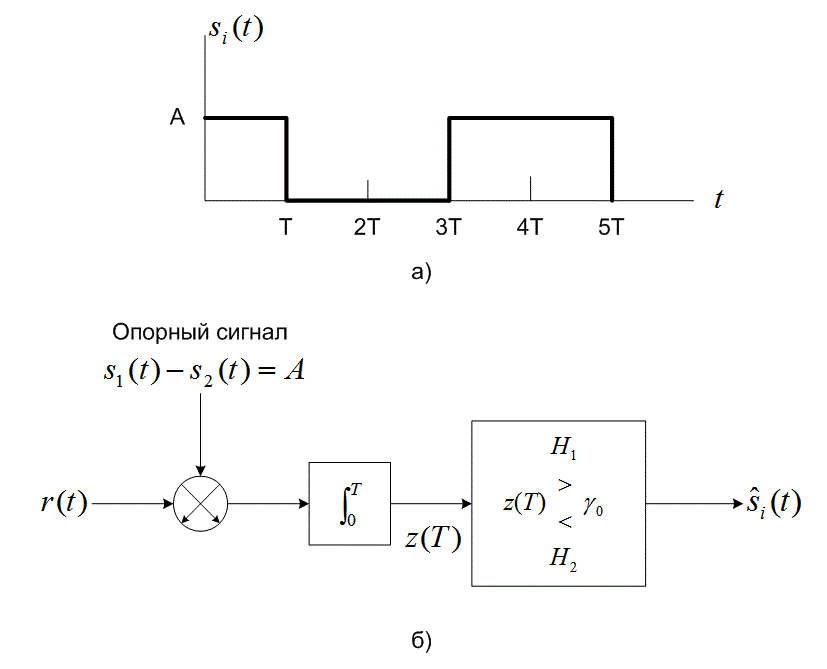
Рис.3.12. Обнаружение при униполярной узкополосной передаче сигналов:
а) пример униполярной передачи сигналов; б) обнаружение с помощью коррелятора
Поскольку в формуле (3.72) ![]() равно нулю в течение периода передачи символа, множество униполярных импульсов полностью удовлетворяет условию, приведенному в уравнении (3.69), а следовательно, они формируют ортогональное множество сигналов. Рассмотрим униполярную передачу сигналов (рис. 3.12, а) и коррелятор (рис. 3.12, б), который может использоваться для обнаружения подобных импульсов. Коррелятор перемножает входящий сигнал
равно нулю в течение периода передачи символа, множество униполярных импульсов полностью удовлетворяет условию, приведенному в уравнении (3.69), а следовательно, они формируют ортогональное множество сигналов. Рассмотрим униполярную передачу сигналов (рис. 3.12, а) и коррелятор (рис. 3.12, б), который может использоваться для обнаружения подобных импульсов. Коррелятор перемножает входящий сигнал ![]() и разность сигналов-прототипов,
и разность сигналов-прототипов, ![]() , после чего результат интегрируется. По окончании периода передачи символа Т устройство дискретизации (включающееся в момент, определенный как верхний предел интегрирования) дает тестовую статистику
, после чего результат интегрируется. По окончании периода передачи символа Т устройство дискретизации (включающееся в момент, определенный как верхний предел интегрирования) дает тестовую статистику ![]() , которая затем сравнивается с порогом
, которая затем сравнивается с порогом ![]() . В случае приема
. В случае приема ![]() и шума AWGN (т.е. когда
и шума AWGN (т.е. когда ![]() ) сигнальный компонент
) сигнальный компонент ![]() находится с помощью уравнения (3.69).
находится с помощью уравнения (3.69).
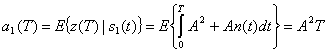
Здесь ![]() - математическое ожидание того, что при принятой выборке
- математическое ожидание того, что при принятой выборке ![]() был передан сигнал
был передан сигнал ![]() . Далее использовано равенство
. Далее использовано равенство ![]() . Подобным образом при
. Подобным образом при ![]() ,
, ![]() . Таким образом, в рассматриваемом случае оптимальный порог принятия решения (см. уравнение (3.32)) равен
. Таким образом, в рассматриваемом случае оптимальный порог принятия решения (см. уравнение (3.32)) равен ![]() . Если тестовая статистика
. Если тестовая статистика ![]() больше
больше ![]() , сигнал считается равным
, сигнал считается равным ![]() ; в противном случае принимается решение, что был передан сигнал
; в противном случае принимается решение, что был передан сигнал ![]() .
.
Из уравнения (3.62) получаем, что энергетический разностный сигнал равен ![]() . Тогда из формулы (3.63) получаем вероятность появления на выходе ошибочного бита.
. Тогда из формулы (3.63) получаем вероятность появления на выходе ошибочного бита.
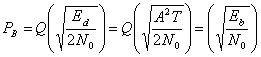 , (3.73)
, (3.73)
где при равновероятной передаче сигналов средняя энергия на бит равна ![]() . Уравнение (3.73) совпадает с уравнением (3.71), полученным с помощью общих рассуждений для ортогональной передачи сигналов.
. Уравнение (3.73) совпадает с уравнением (3.71), полученным с помощью общих рассуждений для ортогональной передачи сигналов.
Отметим, что вне блока перемножения, подобного показанному на рис. 3.12, б, единицей измерения сигнала является вольт. Следовательно, для сигналов напряжения на каждом из двух входов передаточная функция блока перемножения должна иметь размерность 1/вольт, а функция ![]() вне блока перемножения - вольт/вольт в квадрате. Подобным образом вне блока интегрирования также используется единица измерения вольт. Следовательно, для сигнала напряжения в блоке интегрирования передаточная функция интегратора должна иметь размерность 1/секунду, а значит, общая передаточная функция блока перемножения-интегрирования должна иметь размерность 1/вольт-секунда. Итак, для сигнала, поступающего на интегратор и имеющего размерность энергии (вольт в квадрате-секунда), получаем с выхода сигнал, пропорциональный энергии принятого сигнала (вольт/джоуль).
вне блока перемножения - вольт/вольт в квадрате. Подобным образом вне блока интегрирования также используется единица измерения вольт. Следовательно, для сигнала напряжения в блоке интегрирования передаточная функция интегратора должна иметь размерность 1/секунду, а значит, общая передаточная функция блока перемножения-интегрирования должна иметь размерность 1/вольт-секунда. Итак, для сигнала, поступающего на интегратор и имеющего размерность энергии (вольт в квадрате-секунда), получаем с выхода сигнал, пропорциональный энергии принятого сигнала (вольт/джоуль).
3.2.5.2. Биполярная передача сигналов
На рис. 3.13, а приведен пример узкополосной антиподной передачи сигналов, называемой биполярной, где
![]()
![]()
![]()
![]()
![]() (3.74)
(3.74)
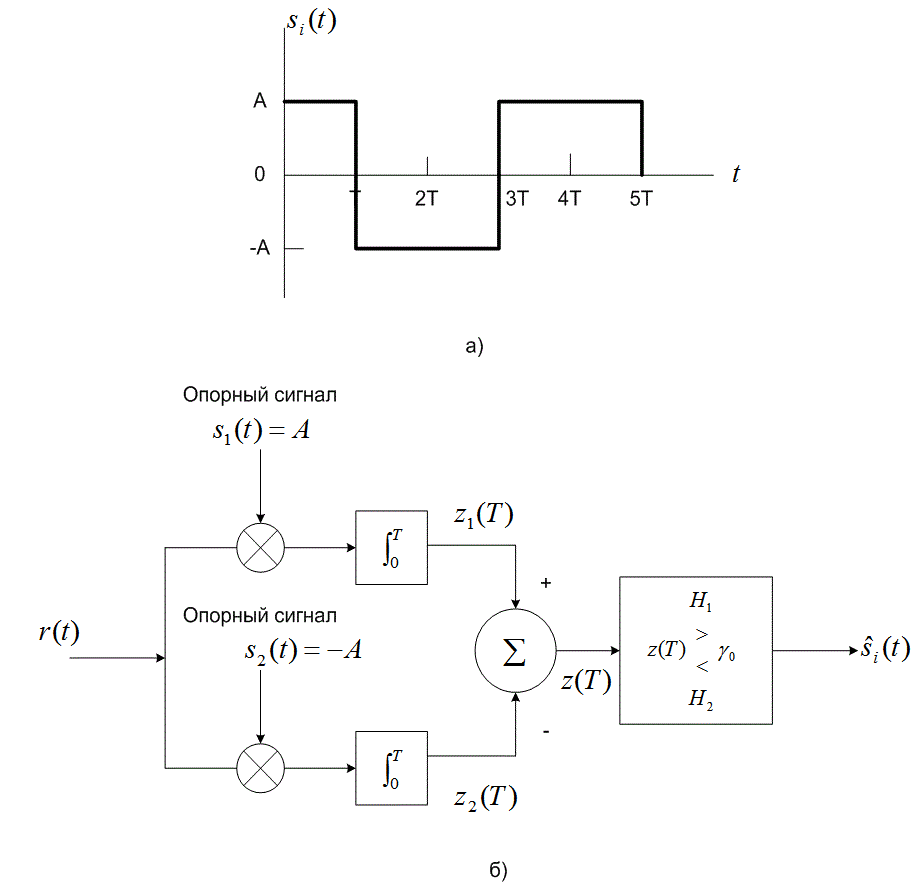
Рис.3.13. Обнаружение при биполярной узкополосной передаче сигналов: а) пример биполярной передачи сигналов; б) обнаружение с помощью коррелятора
Как определялось ранее, термин «антиподный» относится к двоичным сигналам, которые являются зеркальными отображениями друг друга, т.е. ![]() . Приемник-коррелятор таких антиподных сигналов может иметь схему, подобную представленной на рис. 3.13, б. Один коррелятор перемножает входящий сигнал
. Приемник-коррелятор таких антиподных сигналов может иметь схему, подобную представленной на рис. 3.13, б. Один коррелятор перемножает входящий сигнал ![]() и сигнал-прототип
и сигнал-прототип ![]() , после чего интегрирует результат; второй выполняет те же действия с сигналом
, после чего интегрирует результат; второй выполняет те же действия с сигналом ![]() .
.
На рис. 3.13, б изображена сама суть основной функции цифрового приемника. Иными словами, в течение периода передачи символа входящий зашумленный сигнал пускается по множественным различным «проходам» для проверки его корреляции со всеми возможными прототипами. После этого приемник определяет наибольшее выходное напряжение (наилучшее соответствие) и принимает соответствующее, решение относительно значения переданного символа. В бинарном случае имеем два возможных прототипа. В квадратичном случае могут существовать 4 возможности и т.д. На рис. 3.13, б выходы коррелятора обозначены как ![]()
![]() . Тестовая статистика, сформированная из разности выходов коррелятора, выглядит следующим образом.
. Тестовая статистика, сформированная из разности выходов коррелятора, выглядит следующим образом.
![]() (3.75)
(3.75)
Решение принимается с использованием порога, указанного в формуле (3.32). Для антиподных сигналов ![]() ; следовательно,
; следовательно, ![]() . Значит, если тестовая статистика
. Значит, если тестовая статистика ![]() положительна, считается, что передан сигнал
положительна, считается, что передан сигнал ![]() ; если же тестовая статистика отрицательна, считается, что передан сигнал
; если же тестовая статистика отрицательна, считается, что передан сигнал ![]() .
.
Из уравнения (3.62) энергетический разностный сигнал равен ![]() . Следовательно, можем использовать уравнение (3.63) для вычисления вероятности появления ошибочного бита.
. Следовательно, можем использовать уравнение (3.63) для вычисления вероятности появления ошибочного бита.
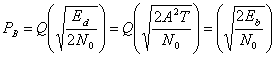 (3.76)
(3.76)
Здесь средняя энергия на бит равна ![]() . Уравнение (3.76) совпадает с уравнением (3.70), полученным с помощью общих рассуждений для ортогональной передачи сигналов.
. Уравнение (3.76) совпадает с уравнением (3.70), полученным с помощью общих рассуждений для ортогональной передачи сигналов.
3.2.5.3. Использование базисных функций для описания передачи сигналов
В корреляторе, приведенном на рис. 3.13, б, в качестве опорных могут использоваться не только сигналы ![]() ; с этой же целью могут применяться базисные функции, описанные в разделе 3.1.3. Проиллюстрируем этот подход на бинарной передаче сигналов с помощью униполярных или биполярных импульсов, поскольку в этом случае все сигнальное пространство можно охарактеризовать одной базисной функцией. Если нормировать пространство, т.е. в уравнении (3.76) положить
; с этой же целью могут применяться базисные функции, описанные в разделе 3.1.3. Проиллюстрируем этот подход на бинарной передаче сигналов с помощью униполярных или биполярных импульсов, поскольку в этом случае все сигнальное пространство можно охарактеризовать одной базисной функцией. Если нормировать пространство, т.е. в уравнении (3.76) положить ![]() , то базисная функция
, то базисная функция ![]() будет равна
будет равна ![]() .
.
Для униполярной передачи импульсов можем записать следующее.
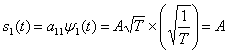
и
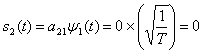
Здесь коэффициенты ![]() , и
, и ![]() равны, соответственно,
равны, соответственно, ![]() и
и ![]() .
.
Для биполярной передачи импульсов можем записать
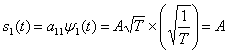
и
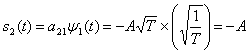
где коэффициенты ![]() и
и ![]() равны, Соответственно,
равны, Соответственно, ![]() и
и ![]() . При использовании антиподных импульсов можно считать, что приемник-коррелятор имеет вид, показанный на рис. 3.12, б, с опорным сигналом, равным
. При использовании антиподных импульсов можно считать, что приемник-коррелятор имеет вид, показанный на рис. 3.12, б, с опорным сигналом, равным ![]() . Итак, при передаче
. Итак, при передаче ![]() , можем записать следующее.
, можем записать следующее.
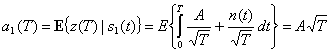
Поскольку ![]() , а значит для антиподной передачи сигналов
, а значит для антиподной передачи сигналов ![]() , то
, то ![]() . Аналогично при приеме сигнала
. Аналогично при приеме сигнала ![]() получаем
получаем ![]() . Если опорные сигналы рассматривать именно таким образом, то математическое ожидание
. Если опорные сигналы рассматривать именно таким образом, то математическое ожидание ![]() равно
равно ![]() (измеряется в нормированных вольтах, пропорциональных принятой энергии). Приведенный подход к описанию коррелятора дает удобное выражение
(измеряется в нормированных вольтах, пропорциональных принятой энергии). Приведенный подход к описанию коррелятора дает удобное выражение ![]() , имеющее те же единицы измерения (вольт), что используются вне блоков перемножения и интегрирования. Еще раз повторим важный момент: на выходе устройства дискретизации (в додетекторной точке) тестовая статистика
, имеющее те же единицы измерения (вольт), что используются вне блоков перемножения и интегрирования. Еще раз повторим важный момент: на выходе устройства дискретизации (в додетекторной точке) тестовая статистика ![]() - это сигнал напряжения, пропорциональный энергии принятого сигнала.
- это сигнал напряжения, пропорциональный энергии принятого сигнала.
На рис. 3.14 показана зависимость ![]() от
от ![]() для биполярной и униполярной передачи сигналов. Существует только два точных способа сравнения этих кривых. Проведем вертикальную линию при некотором данном отношении
для биполярной и униполярной передачи сигналов. Существует только два точных способа сравнения этих кривых. Проведем вертикальную линию при некотором данном отношении ![]() , скажем 10 дБ. Видим, что униполярная передача сигналов дает вероятность
, скажем 10 дБ. Видим, что униполярная передача сигналов дает вероятность ![]() порядка
порядка ![]() , а биполярная – порядка
, а биполярная – порядка ![]() . Нижняя кривая соответствует лучшей достоверности передачи. Можно также провести горизонтальную линию при некотором требуемом уровне
. Нижняя кривая соответствует лучшей достоверности передачи. Можно также провести горизонтальную линию при некотором требуемом уровне ![]() , скажем
, скажем ![]() . Видим, что при униполярной передаче сигналов каждый принятый бит потребует отношения
. Видим, что при униполярной передаче сигналов каждый принятый бит потребует отношения ![]() порядка 12,5 дБ, а при биполярной передаче - не более 9,5 дБ. Разумеется, более низкие требования лучше (требуется меньшая мощность, меньшая полоса). Вообще, более достоверным схемам соответствуют кривые, расположенные ближе к левой и нижней осям. Изучая кривые на рис. 3.14, видим, что биполярная схема имеет выигрыш в 3 дБ по сравнению с униполярной. Это Отличие могло быть предсказано ранее, поскольку отношение
порядка 12,5 дБ, а при биполярной передаче - не более 9,5 дБ. Разумеется, более низкие требования лучше (требуется меньшая мощность, меньшая полоса). Вообще, более достоверным схемам соответствуют кривые, расположенные ближе к левой и нижней осям. Изучая кривые на рис. 3.14, видим, что биполярная схема имеет выигрыш в 3 дБ по сравнению с униполярной. Это Отличие могло быть предсказано ранее, поскольку отношение ![]() в формулах (3.70) и (3.71) отличалось в 2 раза. В главе 4 будет показано, что при обнаружении с использованием согласованного фильтра полосовая антиподная передача сигналов (например, двоичная фазовая манипуляция) дает такое же значение
в формулах (3.70) и (3.71) отличалось в 2 раза. В главе 4 будет показано, что при обнаружении с использованием согласованного фильтра полосовая антиподная передача сигналов (например, двоичная фазовая манипуляция) дает такое же значение ![]() , как и узкополосная антиподная передача сигналов (например, с помощью биполярных импульсов). Также будет показано, что при обнаружении с помощью согласованного фильтра полосовая ортогональная передача сигналов (например, ортогональная частотная манипуляция) дает такое же значение
, как и узкополосная антиподная передача сигналов (например, с помощью биполярных импульсов). Также будет показано, что при обнаружении с помощью согласованного фильтра полосовая ортогональная передача сигналов (например, ортогональная частотная манипуляция) дает такое же значение ![]() , как и узкополосная ортогональная передача сигналов (например, с использованием униполярных импульсов).
, как и узкополосная ортогональная передача сигналов (например, с использованием униполярных импульсов).
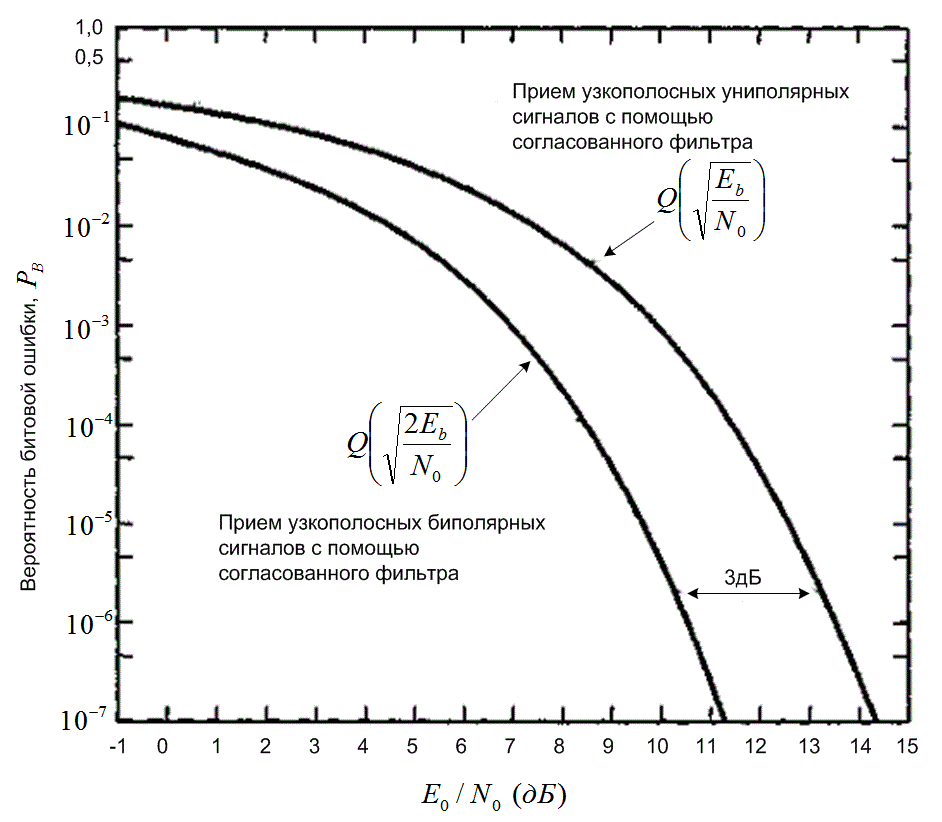
Рис.3.14. Вероятность появления ошибочного бита при униполярной и биполярной передаче сигналов

