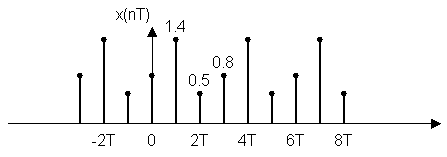
Линейная свертка.

Спектр сигнала на выходе цепи равен произведению входного сигнала на передаточную функцию, т.е.

Y(jω) = X(jω) · H(jω)

В равной мере это относится и к Z–изображениям:

Y(Z) = X(Z) · H(Z)

Но произведению Z–изображений соответствует свертка сигнала:

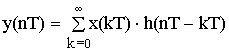– формула линейной свертки.

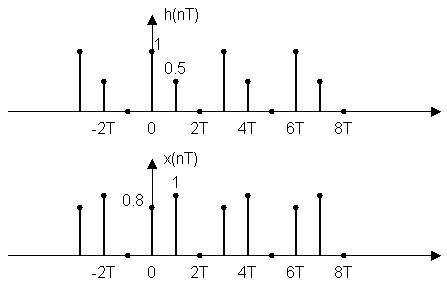
Пример: h(nT) = {1.0; 0.5}

Определить y(nT), если x(nT) = {0.8; 1.0}. Верхний предел можно взять n.

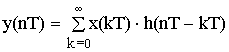
n=0; y(0T) = x(0T)·h(0T) = 0.8·1.0 = 0.8

n=1; y(1T) = x(0T) ·h(1T) + x(1T) ·h(0T) = 0.8·0.5 + 1.0·1.0 = 1.4

n=2; y(2T) = x(0T) ·h(2T) + x(1T) ·h(1T) + x(2T) ·h(0T) =

= 0.8·0 + 1·0.5 + 0·1 = 0.5

Ответ: y(nT) = {0.8; 1.4; 0.5}

Круговая свертка.

Спектр периодического сигнала является дискретным, поэтому спектр на выходе периодического сигнала определяется произведением дискретных спектров.

Y(jkω₁) = X(jkω₁) · H(jkω₁)

Это выражение имеет смысл лишь в том случае, когда периоды всех сигналов (y(nT), x(nT), h(nT)) одинаковы и следовательно число частотных отсчетов будет одинаковым для всех сигналов.

Если периоды сигналов будут разными, то все периоды выравниваются по максимальному периоду, а недостающие отсчеты заменяются нулями.

NT– число отсчетов в периоде, где больше период сигнала.

Произведению дискретных спектров соответствует свертка периодических сигналов на интервале равным одному периоду.

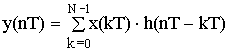– формула круговой свертки.

Сигнал на выходе цепи имеет наибольшее количество отсчетов по сравнению с x(nT) и h(nT), т.е.

если N₁ – число отсчетов x(nT)

N₂ – число отсчетов h(nT),

то N = N₁ + N₂ – 1 – число отсчетов y(nT).

Пример: Исходные данные из предыдущего примера.

x(nT) = {0.8; 1.0} h(nT) = {1.0; 0.5}

N₁ = 2 ; N₂ = 2 ; N = 2 +2 – 1 = 3

X(nT) = {0.8; 1.0; 0} h(nT) = {1.0; 0.5; 0}

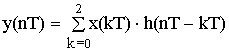
n = 0; y(0T) = x(0T)·h(0T) + x(1T) ·h(-1T) + x(2T) ·h(-2T) =

= 0.8·1 + 1·0 + 0·0.5 = 0.8

n = 1; y(1T) = x(0T)·h(1T) + x(1T) ·h(0T) + x(2T) ·h(-T) =

= 0.8·0.5 + 1·1 + 0·0 = 1.4

n = 2; y(2T) = x(0T)·h(2T) + x(1T) ·h(1T) + x(2T) ·h(0T) =

= 0.8·0 + 1·0.5 + 0·1 = 0.5

y(nT) = {0.8; 1.4; 0.5}