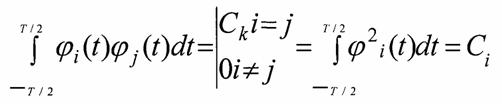1. Функция корреляции - четная функция. В(τ) =В(-τ)

2. В_хх (τ) =σ², где σ²- дисперсия случайного процесса.

3. В_хх(τ)≥В_хх(τ)

4. Если R_xx (τ) = 1 при τ = 0, тогда

R_xx (τ) = 0 при τ ≠ 0, то такой процесс называется чисто случайным процессом.

5. Если стационарный случайный процесс не содержит регулярной составляющей, то его функция корреляции В_хх (τ) →а².

6. Если стационарный случайный процесс содержит регулярную составляющую В_хх (τ) →а², где а² - квадрат амплитуды регулярно составляющей.

7. Функция автокорреляции периодического процесса также является периодической с тем же периодом, что и сам процесс. В_ху периодический процесс не зависит от его начальной фазы.

ИНТЕРВАЛ КОРРЕЛЯЦИИ

Для стационарных случайных процессов можно указать такой промежуток времени Δτ, что как только Δτ > τ, то его отдельные значения становятся независимыми.

Этот промежуток времени Δτ, в пределах которого существует взаимосвязь между отельными значениями случайного процесса, называется интервалом корреляции.

Δτ - определяется шириной основания прямоугольника с единичной высотой, площадь которого равно площади, ограниченной кривой В_хх.

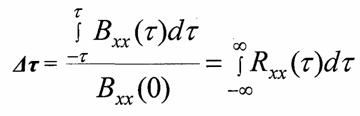
РАЗЛОЖЕНИЕ СИГНАЛОВ НА ЭЛЕМЕНТАРНЫЕ СОСТАВЛЯЮЩИЕ.

Реальные сигналы носят случайные характер и имеют сложную форму

1. Элементарные сигналы должны быть взаимно независимыми, и будучи умноженными на а_к, мы должны получить S(t).

2. Значения весовых коэффициентов а_к не должны зависеть от количества элементных составляющих.

Этим двум требованиям отвечает ортогональная функция.