7.1. Принцип действия асинхронного двигателя

7.2. Статические характеристики асинхронного двигателя

7.3. Управление асинхронными двигателями

7.3.1. Управление трехфазными асинхронными двигателями

7.3.2. Управление двухфазными асинхронными двигателями

7.1. Принцип действия асинхронного двигателя

Двигатели переменного тока делятся на синхронные и асинхронные двигатели. Асинхронные двигатели (АД) в свою очередь делятся на двух и трехфазные, из которых в качестве исполнительных двигателей в системах автоматического управления в основном применяются маломощные двигатели до 300 Вт.

Их преимущества перед ДПТ: малая инерционность, бесконтактность, дешевизна.

Их недостатки в сравнении с ДПТ: большие тепловые потери, малый пусковой момент, нелинейные характеристики.

Принцип действия рассмотрим на примере двухфазного асинхронного двигателя, с полым ротором в виде алюминиевого стакана. На статоре этого двигателя расположены две обмотки. Эти обмотки расположены на магнитопроводе под углом 90⁰ друг к другу. На эти обмотки подаются синусоидальные напряжения, сдвинутые по фазе на 90⁰ друг к другу. Под действием этих напряжений в обмотках протекают токи I₁, I₂, также синусоидальные и сдвинутые по фазе на 90⁰. Будем считать, что амплитуды их равны. Эти токи, в свою очередь, создают в магнитопроводе два пульсирующих вектора магнитной индукции и, соответственно два магнитных потока, равных по амплитуде и сдвинутые по фазе на 90⁰ друг к другу в пространстве и времени. Они суммируются, и создается результирующий магнитный поток, имеющий постоянную амплитуду и вращающийся по окружности с частотой w, где w=2p¦, а ¦ - частота сети.

Рассмотрим получение кругового вращающегося магнитного поля в случае двухфазной системы (рис. 70).

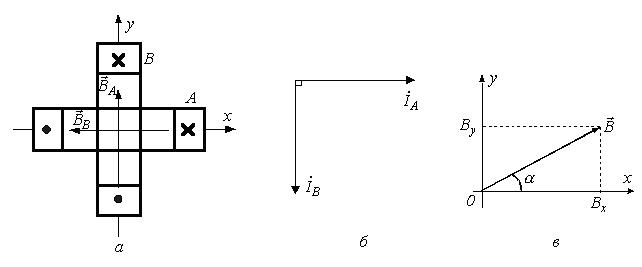
Рис. 70. Двухфазная система

При пропускании через катушки гармонических токов каждая из них в соответствии с вышесказанным будет создавать пульсирующее магнитное поле. Векторы В_А и В_В, характеризующие эти поля, направлены вдоль осей соответствующих катушек, а их амплитуды изменяются также по гармоническому закону. Если ток в катушке В отстает от тока в катушке А на 90⁰, то В_А= В_msin(wt) и В_В= В_msin(wt-90⁰).

Найдем проекции результирующего вектора магнитной индукции Вна оси x и y декартовой системы координат, связанной с осями катушек:

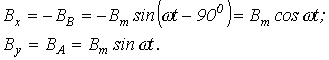
Модуль результирующего вектора магнитной индукции в соответствии с рис. 70 равен,

при этом для тангенса угла a , образованного этим вектором с осью абсцисс, можно записать

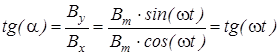, откуда a=wt.

Полученные соотношения показывают, что вектор результирующего магнитного поля неизменен по модулю и вращается в пространстве с постоянной угловой частотой , описывая окружность, что соответствует круговому вращающемуся полю.

Симметричная трехфазная система катушек также позволяет получить круговое вращающееся магнитное поле. Рис. 71. Каждая из катушек А, В и С при пропускании по ним гармонических токов создает пульсирующее магнитное поле. Катушки питаются трехфазной системой токов с временным сдвигом по фазе на 120⁰. Поэтому для мгновенных значений индукций катушек имеют место соотношения

; ; .

Произведя аналогичные расчеты, получим, что модуль результирующего вектора магнитной индукции равен В=1,5 В_m, и также вращается в пространстве с постоянной угловой частотой ,

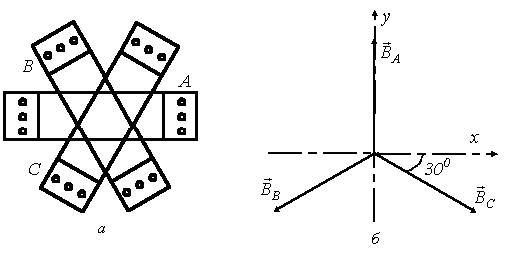
Рис. 71. Трехфазная система

Силовые линии вращающегося магнитного поля пересекают ротор двигателя, выполненный, например, в виде алюминиевого стакана. В материале ротора наводятся вихревые токи, которые взаимодействуют с вращающимся магнитным потоком статоре и создают движущий момент. Под действием этого момента ротор начинает раскручиваться и набирает скорость до тех пор, пока движущий момент не будет уравновешен моментом, создаваемым нагрузкой.

Скорость вращения ротора асинхронного двигателя всегда меньше скорости вращения поля, так как в случае их равенства результирующий магнитный поток будет неподвижен относительно ротора, вихревых токов не будет, и, следовательно, не будет движущего момента. Поэтому двигатель называется асинхронным. Величина отставания скорости вращения ротора от скорости вращения поля характеризуется скольжением.

При заторможенном роторе S=1, в идеальном случае при вращении со скоростью поля S=0.

Используются различные конструкции ротора АД. Есть трехфазные АД с фазным ротором, при этом на роторе также намотаны три, пространственно сдвинутых обмотки. В эти обмотки обычно включают внешние сопротивления (реостаты), которыми ограничивается пусковой ток и может регулироваться скорость вращения ротора. Двухфазные АД изготавливают с короткозамкнутой обмоткой: в виде беличьего колеса; в виде вала или стакана из проводящего материала. .Рис 72, 73, 74.

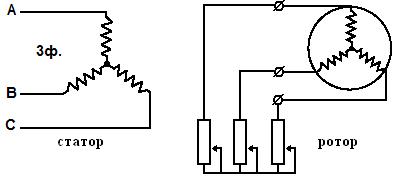
Рис. 72. Трехфазный АД с фазным ротором

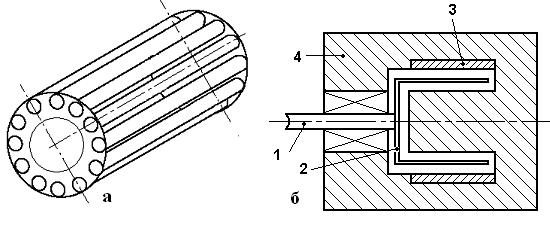
Рис. 73. Ротор АД в виде беличьей клетки (а) и в виде стакана (б)

7.2. Статические характеристики асинхронного двигателя

Под действием электромагнитной индукции в обмотках или элементах короткозамкнутого ротора ("беличьей клетке") индуктируются вторичные ЭДС и токи частоты ω₂, которые взаимодействуют с вращающимся магнитным полем, создается электромагнитный момент M, что приводит к вращению ротора с частотой ω₁. Рассмотрим для примера модель двигателя, в которой число пар полюсов p=1.

Частота индуцируемых во вторичной обмотке (роторе) ЭДС и токов ω₂ зависит от скольжения S:

.

Эквивалентная схема цепи ротора в рабочем режиме показана на Рис 74.

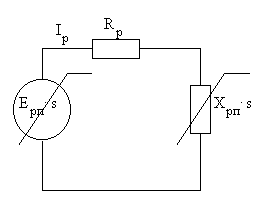
Рис. 74. Схема цепи ротора АД

Она содержит изменяемый источник ЭДС E_рп·S и изменяемое индуктивное сопротивление x_р=x_рп·S. Они изменяются при изменении скольжения S (частоты вращения), а активное сопротивление R_p не изменяется.

Мы можем привести рабочий режим двигателя к режиму неподвижного ротора и рассматривать асинхронную машину как обычный трансформатор с неподвижными обмотками; в результате преобразования получаем эквивалентную схему. АД, с учетом параметров обмотки статора.

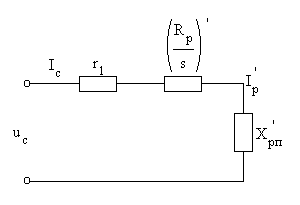
Рис. 75. Эквивалентная электрическая схема АД

На схеме обозначены: - приведенные сопротивления, n- коэффициент трансформации, а r₁- активное сопротивление цепи статора. На основании этой схемы получим выражение для тока ротора

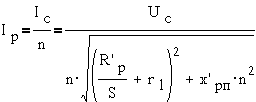
Выражение для вращающегося момента можем получить из энергетического уравнения M·ω₁= M·ω+m₁·I_p²·R_p, где m₁- количество фаз. Левая часть уравнения - электромагнитная мощность, а правая - механическая плюс электрическая мощности.

Подставляя сюда выражения для тока ротора, получим аналитическое выражение для электромагнитного момента и, если пренебречь активным сопротивлением обмотки статора, получается уравнение Клосса, отражающее зависимость электромагнитного момента от скольжения. Выражение для момента двигателя представлено через параметры критической точки:

.

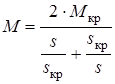Скольжение, соответствующее максимальному моменту, называется критическим и обозначается S_K или S_M.

Критическое скольжение за зависит от соотношение активного и индуктивного сопротивлений ротора. При r₁=0 получим 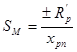и .

Вид зависимости электромагнитного момента и тока ротора от скольжения показан на. рис. 76.

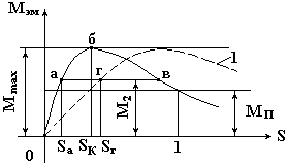
Рис. 76. Зависимость электромагнитного момента АД от скольжения

Пусть исполнительный механизм, приводимый во вращение данным двигателем, создает противодействующий тормозной момент М2. На рис. 76 имеются две точки, для которых справедливо равенство М_эм = М₂; это точки а и в.

В точке а двигатель работает устойчиво. Если двигатель под влиянием какой-либо причины уменьшит частоту вращения, то скольжение его возрастет, вместе с ним возрастет вращающий момент. Благодаря этому частота вращения двигателя повысится, и вновь восстановится равновесие М_эм = М₂;.

В точке в работа двигателя не может быть устойчива: случайное отклонение частоты вращения приведет либо к остановке двигателя, либо к переходу его в точку а. Следовательно, вся восходящая ветвь характеристики является областью устойчивой работы двигателя, а вся нисходящая часть - областью неустойчивой работы. Точка б, соответствующая максимальному моменту, разделяет области устойчивой и неустойчивой работы.

Максимальному значению вращающего момента соответствует критическое скольжение S_k. Скольжению S = 1 соответствует пусковой момент. Если величина противодействующего тормозного момента М₂ больше пускового МП, двигатель при включении не запустится, останется неподвижным. Еще выводы:

• величина максимального вращающего момента не зависит от активного сопротивления цепи ротора;
• с увеличением активного сопротивления цепи ротора максимальный вращающий момент, не изменяясь по величине, смещается в область больших скольжений;
• вращающий момент пропорционален квадрату напряжения сети.

Механической характеристикой асинхронного двигателя называется зависимость частоты вращения двигателя от момента на валу n₂ = f (M₂). Механическую характеристику получают при условии U - const, w₁ - const. На рис. 77 изображена типичная механическая характеристика асинхронного двигателя.

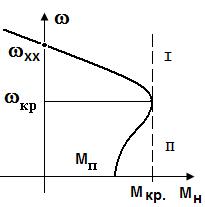
Рис. 77. Механическая характеристика асинхронного двигателя

На механической характеристике АД можно выделить два участка, которые разделены значением М_кр:

• режим устойчивой работы,
• режим неустойчивой работы.

Для каждого двигателя есть свое значение М_кр. При работе двигателя на первом участке М_кр.< М_н<0. и двигатель может развить вращающий момент, компенсирующий момент нагрузки. При работе двигателя на втором участке М_кр.> М_н происходит торможение и двигатель останавливается.

Различают 3 статических режима работы:

• Двигательный. В этом режиме направление вращения ротора и поля совпадают и . w_p<w.
• Режим генераторного торможения. В этом режиме направление вращения ротора и поля совпадают, но . w_p>w. Это возможно, если момент нагрузки поменяет знак. Двигатель не потребляет, а отдает энергию.
• Режим торможения противовключением. Реализуется, если в обмотке управления изменится фаза на 180⁰, после этого вращающий момент поменяет знак и будет тормозить ротор.

7.3. Управление асинхронными двигателями

Есть различные способы управления асинхронными двигателями:

• параметрическое управления трехфазными асинхронными двигателями.
• симметричное частотное управление,
• несимметричное амплитудно–фазовое управление,

7.3.1. Управление трехфазными асинхронными двигателями

1. Рассмотрим сначала способы управления трехфазными асинхронными двигателями. Первый способ используется для двигателей с фазным ротором. Критическое скольжение S_kr определяется активным сопротивлением ротора R_r. Если R_r изменять, то будет изменяться наклон механической характеристики и соответственно скорость вращения ротора. Рис.78..

Рис. 78. Механическая характеристика асинхронного двигателя

Такой способ используется при пуске двигателя под нагрузкой, когда желательно, чтобы пусковой момент был максимальным. Для регулирования он применяется редко, т. к. велики тепловые потери в роторной цепи. Другим способом регулирования скорости является изменение напряжения на статоре, для АД вращающий момент изменяется пропорционально квадрату напряжения. При этом изменение напряжения питания мало влияет на частоту вращения ротора на рабочем участке и диапазон управления напряжением весьма ограничен.

2. Плавное регулирование скорости в широких пределах с сохранением достаточной жесткости характеристик возможно только при частотном управлении.. Изменяя частоту вращения поля ω₁, можно изменять частоту вращения ротора ω при этом желательно, чтобы. жесткость характеристики не изменялась. Для этого одновременно с частотой, изменяют напряжение питания U_c так, чтобы их отношение оставалось постоянным U_c/w₁=const.

Такое управление называется пропорциональным частотным управлением. Вид механических характеристик при пропорциональном управлении показан на рис. 79.

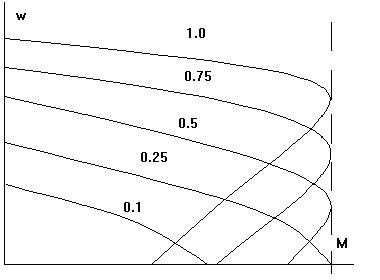
Рис. 79. Частотное управление асинхронным двигателем

При симметричном частотном управлении требуется специальное устройство преобразователь частоты, формирующий на выходе синусоидальный сигнал с изменяемой частотой w. Поле при этом управлении круговое, амплитуды на обмотках равны. Диапазон частот должен быть ограничен, так как при низких частотах падает индуктивное сопротивление обмоток и сильно растет ток, для высоких частот тоже существуют конструктивные и электрические ограничения. Поэтому при частотном управлении на самом деле идет управление по двум параметрам: частоте и амплитуде.

Функциональная схема частотного управления представлена на. на рис. 80. Она состоит из управляемого выпрямителя УВ, преобразующего напряжение переменного тока частотой 50 Гц в напряжение постоянного тока U_п, величина которого может регулироваться устройством управления УУ. Автономный инвертор АИ преобразует напряжение U_п в трехфазное напряжение изменяемой частоты f₁. Управляющее устройство, изменяя частоту f_1в в зависимости от задания ω_з, изменяет также и напряжение U_п так, чтобы их отношение оставалось постоянным. Система управления может иметь обратную связь по скорости вращения через тахогенератор ТГ.

Более совершенным, чем пропорциональное управление, является частотно-токовое управление, при котором контролируется, кроме частоты вращения, ток якоря от датчика, что позволяет оставлять постоянным поток при изменении частоты f₁ и нагрузки.

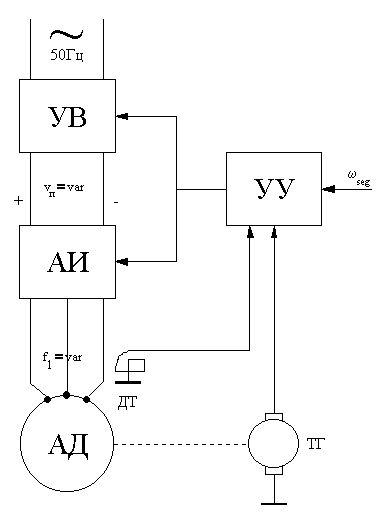
Рис. 80. Функциональная схема частотного управления асинхронным двигателем

7.3.2. Управление двухфазными асинхронными двигателями

В исполнительных приводах малой мощности широко в основном используются управляемые и неуправляемые двухфазные асинхронные двигатели. Эти , двигатели имеют две обмотки: одна включается в сеть непосредственно и называется обмоткой возбуждения (главной). На обмотку управления (вспомогательную), сдвинутую на статоре на90^o градусов напряжение подается через фазосдвигающий элемент. Ротор всегда короткозамкнутый.

При таком способе управления есть разные варианты: амплитудное, фазовое и амплитудно–фазовое управление. При этих способах. на второй обмотке можно менять амплитуду напряжения, его фазу или оба параметра одновременно. При этом поле превращается из кругового в эллиптическое. При этом наряду с напряжениями и токами прямой последовательности фаз, создающими двигательный режим, возникает напряжение и токи обратной последовательности, вызывающие торможение. Таким образом, меняя степень асимметрии, можно регулировать скорость двигателя. Рис.81.

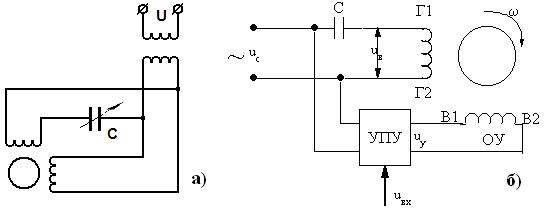
Рис. 81. Конденсаторный и управляемый двухфазные АД

При U_y=0, получим пульсирующее поле и w=0. Наиболее распространенным способом является конденсаторное управление. Чаще всего используется амплитудное несимметричное управление, когда U_B=U_C, а U_γ=α·U_c, где α меняется от 0 до 1. Можно получить выражения для вращающего момента при амплитудном управлении, аналогичное уравнению Клосса.

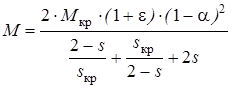
При симметрии напряжений, когда α=1, из этого уравнения получим нормальное уравнение выражение для асинхронной машины Так как в двухфазных двигателях S_M>1, то при α=0, т.е. при отключении обмотки управления двигатель тормозится, и останавливается при S=1.

Механические и регулировочные характеристики асинхронного двигателя. нелинейны. Их заменяют в рабочей области прямыми:

M = b₁U-b₂w.

Коэффициенты b₁ и b₂ определяют по паспортным данным АД. В момент пуска М =М_п, w = 0, поэтому

М_п = b₁∙U_n и b₁ = М_н/U_n.

Для номинального режима аналогично получим, учитывая , что P_N = M_N∙w_N,

M_N = М_п -b₂∙ w_N и b₂∙ = (М_п -M_N)/w_N.

Мы получим уравнение линеаризованной механической характеристики :

w = (b_1/ b₂)∙U-M/ b₂.

Механические и регулировочные характеристики асинхронного двигателя показаны на рис. 82.

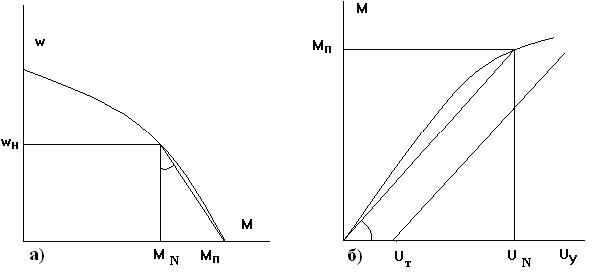
Рис. 82. Механическая и регулировочная характеристики двухфазного АД

После линеаризации асинхронный двигатель может быть представлен как линейная динамическая система, описываемая следующими уравнениями (b_w = b₁, b_u = b₂):

.

Рассмотрим случай, когда сухое трение отсутствует и есть только скоростное трение, то есть М_Т = F∙w. Заменив . и проведя преобразования получим:

.

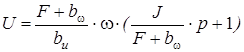Отсюда выражение для передаточной функции

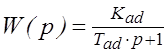, где коэффициент передачи 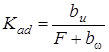и электромеханическая постоянная времени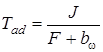

Этой передаточной функции соответствует структурная схема и переходный процесс, представленные на рис. 83.

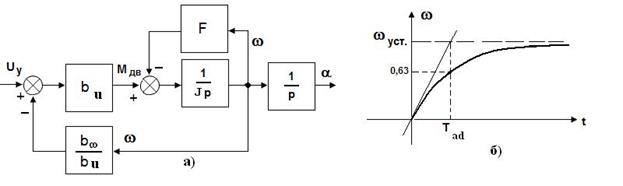
Рис. 83. Структурная схема и переходный процесс АД