Особенностью радиотехнических информационных систем является то, что передача сигналов и их прием происходит на фоне мешающих факторов – помех. Действие помех снижает качество приема сигналов, а, следовательно, и эффективность всей системы. Поэтому борьба с помехами в РТИС является одной из важнейших задач.

Методы борьбы с помехами при приеме и обработке сигналов основываются на различии структуры сигнала и помехи. Выделяют три основных вида задач борьбы с помехами в РТИС. К первому виду относятся задачи обнаружения сигнала на фоне помех. Такие задачи встречаются, например, в радиолокации. Второй вид задач состоит не только в обнаружении, но и различении двух или более сигналов. Задачи этого вида встречаются в той же радиолокации для различения сигналов от нескольких целей или при передаче информации цифровыми сигналами, которые представляют собой последовательности радиоимпульсов, отличающихся либо амплитудами (дискретная амплитудная модуляция), либо частотами (дискретная частотная модуляция), либо текущими фазами (дискретная фазовая модуляция).

И наконец, к третьему виду задач относятся задачи оценки параметров сигналов. В радиолокации, например, оценка частоты отраженного от цели зондирующего радиоимпульса позволяет судить о скорости движения объекта (эффект Доплера), а в системах передачи оценка временного положения импульсов кодовой комбинации позволяет решить задачу синхронизации передающего и приемного устройств.

Мы ограничимся рассмотрением задачи обнаружения детерминированного сигнала на фоне случайных помех. Задача формулируется следующим образом: на вход приемного устройства на интервале наблюдения , где – длительность сигнала, поступает колебание

(7.1)

где – детерминированный сигнал известной формы,

– помеха.

Необходимо найти алгоритм обработки и схемную реализацию приемного устройства, обеспечивающего оптимальные условия установления факта присутствия сигнала в смеси сигнала и помехи.

Прежде, чем приступить к решению задачи, определим критерий оптимальности обнаружения. Очевидно, если сигнал и помеха на входе приемного устройства некоррелированы, средняя мощность колебания равна средней мощности сигнала

, (7.2)

и средней мощности помехи, которая, как известно, равна дисперсии случайного процесса, описывающего помеху

. (7.3)

Отношение

, (7.4)

называется отношением сигнал/помеха на входе приемного устройства.

Если приемное устройство является линейным, то в соответствии с принципом суперпозиции выходное колебание

, (7.5)

и на выходе также можно определить отношение сигнал/помеха, как отношение:

. (7.6)

Тогда задача оптимального обнаружения сигнала на фоне помехи сводится к определению характеристик линейного устройства (линейного фильтра), обеспечивающего максимальное отношение сигнал/помеха на его выходе. Такое линейное устройство получило название оптимального линейного фильтра.

Как известно, одной из важнейших характеристик линейной цепи является ее импульсная характеристика . Линейный фильтр с импульсной характеристикой осуществляет преобразование как детерминированного сигнала , так и помехи . Найдем импульсную характеристику фильтра, осуществляющего преобразование детерминированного сигнала . Детерминированная составляющая сигнала на выходе линейного фильтра в любой момент времени определяется выражением

. (7.7)

Поскольку линейный фильтр должен обеспечить максимальное отношение сигнал/помеха (7.6) или что то же самое

. (7.8)

где – максимальное абсолютное значение сигнала на выходе фильтра,

– среднеквадратичное значение помехи,

постараемся выбрать такую функцию , чтобы величина в момент достигала максимального значения. Для этого воспользуемся неравенством Коши – Буняковского

, (7.9)

причем равенство достигается при , где – коэффициент пропорциональности.

Применив (7.9) к правой части (7.7), получим

. (7.10)

При этом равенство в (7.10)будет иметь место при

, (7.11)

и следовательно левая часть (7.10), а значит и достигает максимального значения.

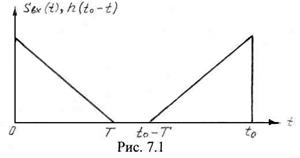
Из выражения (7.11) следует, что импульсная характеристика фильтра, осуществляющего оптимальную обработку детерминированного сигнала , с точностью до масштабного множителя повторяет форму сигнала и является зеркальным ее отображением, сдвинутым по оси времени на . На рис. 7.1 изображены в качестве примера линейно спадающий сигнал и импульсная характеристика соответствующего фильтра. Фильтр, обладающий импульсной характеристикой (7.11) называется согласованным фильтром. Поскольку для физически реализуемого фильтра при (отклик на выходе фильтра не может появиться ранее появления сигнала) сдвиг во времени .

Обычно при реализации согласованного фильтра выбирается и (7.11) принимает вид

. (7.12)

Осуществляя замену переменной можно получить эквивалентное выражение импульсной характеристики фильтра

,

или просто

. (7.13)

Поскольку момент времени соответствует максимальному значению выходного сигнала, этот максимум достигается после окончания воздействия входного сигнала, т.е. для обеспечения максимального отклика фильтр должен обработать весь сигнал.

Комплексный коэффициент передачи согласованного фильтра определяется преобразованием Фурье импульсной характеристики

.

Подстановка в это выражение выражения (7.13) после элементарных преобразований дает

, (7.14)

откуда следует выражение для амплитудно-частотной характеристики фильтра

. (7.15)