5.1. Элементы теории вероятностей
5.2. Случайные процессы и их вероятностные характеристики
5.3. Энергетический спектр случайного процесса
5.5. Эффективная ширина спектра и интервал корреляции
5.6. Белый шум и его характеристики
5.7. Узкополосный случайный процесс
5.8. Вероятностные характеристики огибающей и начальной фазы узкополосного СП
5.1. Элементы теории вероятностей
На практике все сигналы, которые предназначены для передачи информации, носят случайный характер. Именно в случайности изменения сигналов заложена информация, которую необходимо передать получателю. Помимо этого, при передаче сигналов действуют помехи, которые также носят случайный характер.
В отличие от детерминированных сигналов значения случайного сигнала в некоторый момент времени невозможно предсказать точно. Вместе с тем, описание таких сигналов возможно в вероятностном смысле через усредненные (статистические) характеристики. Поэтому, прежде чем перейти к изучению случайных сигналов целесообразно рассмотреть основные положения теории вероятностей.
Подобно тому, как в алгебре основным понятием является число, а в геометрии – точка, линия, плоскость, в теории вероятностей основным понятием является случайное событие, которое при проведении эксперимента может произойти, а может и не произойти. Если, например, проводится эксперимент, включающий серию из n испытаний радиотехнического устройства, то результатом каждого испытания может быть либо рабочее состояние устройства, либо его отказ, которые представляют собой события. Но при каждом конкретном испытании отказ может произойти, а может и не произойти. В этом смысле отказ является случайным событием. Обозначим случайное событие буквой ![]() .
.
Центральным в теории вероятностей является определение частости (или частоты) наступления события ![]()
![]() , (5.1)
, (5.1)
где ![]() – число испытаний, соответствующих наступлению со бытия
– число испытаний, соответствующих наступлению со бытия ![]() ,
,
![]() – общее число все проведенных испытаний.
– общее число все проведенных испытаний.
При достаточно большом числе всех проведенных испытаний (теоретически при ![]() ) частость наступления события
) частость наступления события ![]() отождествляется с вероятностью
отождествляется с вероятностью
![]() . (5.2)
. (5.2)
Из данного определения следует, что
![]() , (5.3)
, (5.3)
т.е. вероятность является неотрицательной величиной, принимающей значение в диапазоне чисел от 0 до 1.
Событие ![]() , для которого
, для которого ![]() , называется невозможным, а событие для которого
, называется невозможным, а событие для которого ![]() – достоверным.
– достоверным.
Понятие вероятности можно распространить на совокупность событий. Если ![]() – множество всех случайных событий, то
– множество всех случайных событий, то ![]() – вероятность наступления события
– вероятность наступления события ![]() . В рассмотренном примере
. В рассмотренном примере ![]() , где
, где ![]() – отказ устройства,
– отказ устройства, ![]() – рабочее состояние.
– рабочее состояние.
Множество ![]() событий образуют полную группу, если в результате испытания одно из событий множества наступит обязательно. События рассмотренного выше примера образуют полную группу. Очевидно, для полной группы событий справедливо равенство
событий образуют полную группу, если в результате испытания одно из событий множества наступит обязательно. События рассмотренного выше примера образуют полную группу. Очевидно, для полной группы событий справедливо равенство
![]() .
.
События ![]() и
и ![]() называются несовместными, если появление одного из них исключает появление другого. События
называются несовместными, если появление одного из них исключает появление другого. События ![]() и
и ![]() рассмотренного примера являются несовместными. Вероятность наступления одного из них, т.е. события
рассмотренного примера являются несовместными. Вероятность наступления одного из них, т.е. события ![]() или события
или события ![]() , или …, события
, или …, события ![]() , …, или события
, …, или события ![]() равна сумме вероятностей этих событий
равна сумме вероятностей этих событий
![]() . (5.5)
. (5.5)
Если в результате эксперимента возможно одновременное наступление событий, например, при включении радиоприемника он является исправным (событие ![]() ) и настроен на произвольную частоту (событие
) и настроен на произвольную частоту (событие ![]() ), то такие события называются совместными. В этом случае говорят, что событие
), то такие события называются совместными. В этом случае говорят, что событие ![]() влечет за собой событие
влечет за собой событие ![]() и такая ситуация обозначается
и такая ситуация обозначается ![]() . Вероятность наступления события
. Вероятность наступления события ![]() , если произошло событие
, если произошло событие ![]() называется условной вероятностью
называется условной вероятностью 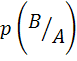 . Очевидно, вероятность одновременного наступления совместных событий
. Очевидно, вероятность одновременного наступления совместных событий ![]() и
и ![]() определяется соотношением
определяется соотношением
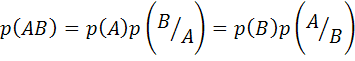 . (5.6)
. (5.6)
События ![]() и
и ![]() называются независимыми, если наступление одного из них не связано с наступлением другого. Вероятность наступления двух независимых совместных событий равна
называются независимыми, если наступление одного из них не связано с наступлением другого. Вероятность наступления двух независимых совместных событий равна
![]() . (5.7)
. (5.7)
Отсюда следует, что для независимых совместных событий условная вероятность 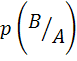 равна безусловной вероятности
равна безусловной вероятности ![]() .
.
Вероятность события ![]() , которое может наступить с одним из событий
, которое может наступить с одним из событий ![]() , образующих полную группу несовместных событий, называемых гипотезами, определяется формулой полной вероятности
, образующих полную группу несовместных событий, называемых гипотезами, определяется формулой полной вероятности
![]() . (5.8)
. (5.8)
Вероятность наступления гипотезы ![]() , после того как наступило событие
, после того как наступило событие ![]() , определяется формулой Байеса
, определяется формулой Байеса
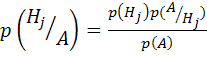 , (5.9)
, (5.9)
где ![]() вычисляется в соответствии с (5.8).
вычисляется в соответствии с (5.8).
Случайные события характеризуют эксперимент с качественной стороны. На практике пользуются количественной оценкой результата. Если в результате эксперимента наступает или не наступает событие ![]() (в рассмотренном примере отказ радиотехнического устройства), этому случайному событию можно поставить в соответствие величину, принимающую только два значения: 1 или 0 в зависимости от того, произошло событие или нет. Так как событие
(в рассмотренном примере отказ радиотехнического устройства), этому случайному событию можно поставить в соответствие величину, принимающую только два значения: 1 или 0 в зависимости от того, произошло событие или нет. Так как событие ![]() случайно, случайной будет и величина (СВ), оценивающая результат эксперимента. Очевидно, вероятность наступления события
случайно, случайной будет и величина (СВ), оценивающая результат эксперимента. Очевидно, вероятность наступления события ![]() в рассматриваемом примере совпадает с вероятностью того, что случайная величина принимает значение, равное 1.
в рассматриваемом примере совпадает с вероятностью того, что случайная величина принимает значение, равное 1.
Обозначим случайную величину через ![]() , а значения, которые она может принимать,− через
, а значения, которые она может принимать,− через ![]() . Если случайная величина
. Если случайная величина ![]() принимает значения из множества
принимает значения из множества ![]() , элементы которого можно перенумеровать, то такая случайная величина называется дискретной СВ. Если же множество
, элементы которого можно перенумеровать, то такая случайная величина называется дискретной СВ. Если же множество ![]() значений непрерывно, т.е. перенумеровать значения невозможно, то такая величина называется непрерывной СВ.
значений непрерывно, т.е. перенумеровать значения невозможно, то такая величина называется непрерывной СВ.
Как дискретная, так и непрерывная СВ полностью характеризуются законами распределения. Функцией распределения (интегральным законом) дискретной СВ называется зависимость
![]() , (5.10)
, (5.10)
т.е. зависимость вероятности того, что случайная величина ![]() не превосходит значения
не превосходит значения ![]() , где
, где ![]() принимает значения от
принимает значения от ![]() до
до ![]() .
.
Рядом распределения дискретной СВ называется совокупность всех возможных значений ![]() и соответствующих им вероятностей
и соответствующих им вероятностей
![]() . (5.11)
. (5.11)
Ряд распределения задается либо выражением (5.11), либо в виде таблицы. Очевидно
![]() . (5.12)
. (5.12)
Функция распределения непрерывной СВ представляет собой зависимость
![]() , (5.13)
, (5.13)
и является интегральным законом распределения непрерывной СВ.
Плотностью распределения непрерывной СВ называется зависимость
![]() , (5.14)
, (5.14)
где ![]() , и представляет собой отношение вероятности
, и представляет собой отношение вероятности ![]() того, что непрерывная СВ будет находиться в пределах элементарного интервала
того, что непрерывная СВ будет находиться в пределах элементарного интервала ![]() к величине этого интервала. Если функция
к величине этого интервала. Если функция ![]() непрерывна и интервал значений СВ составляет (
непрерывна и интервал значений СВ составляет ( ![]() ), то функция распределения и плотность распределения связаны между собой соотношениями
), то функция распределения и плотность распределения связаны между собой соотношениями
![]() , (5.15)
, (5.15)
![]() . (5.16)
. (5.16)
Из (5.16) следует, что плотность распределения представляет собой дифференциальный закон распределения вероятностей.
На рис. 5.1 изображены графики функции распределения и ряда распределения дискретной СВ (рис. 5.1а,б) и функции распределения и плотности распределения (рис. 5.1в,г) непрерывной СВ.
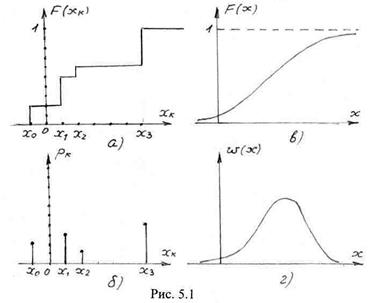 Основные свойства функции распределения:
Основные свойства функции распределения:
− функция распределения (для дискретной СВ – ступенчатая, для непрерывной СВ – непрерывная) является монотонно-возрастающей неотрицательной функцией;
− при ![]() для дискретной СВ и
для дискретной СВ и ![]() для непрерывной СВ функция распределения равна нулю;
для непрерывной СВ функция распределения равна нулю;
− при ![]() для дискретной СВ и
для дискретной СВ и ![]() для непрерывной СВ функция распределения
для непрерывной СВ функция распределения ![]() ;
;
− вероятность попадания СВ в интервал (a,b) равна
![]() . (5.16)
. (5.16)
Основные свойства плотности распределения вероятностей непрерывной СВ:
− плотность вероятности величина неотрицательная, т.е.
![]() , при
, при ![]() ;
;
− вероятность попадания непрерывной СВ в интервал (a,b) равна
![]() . (5.17)
. (5.17)
Отсюда следует, что вероятность попадания СВ в интервал ( ![]() )
)
![]() . (5.18)
. (5.18)
Выражение (5.18) представляет собой условие нормировки. Это означает, что площадь под кривой ![]() равна единице.
равна единице.
Хотя законы распределения в полной мере характеризуют случайную величину, на практике более широко используются числовые характеристики, получаемые усреднением значений самой СВ. числовые характеристики СВ называют моментами. Различают начальные и центральные моменты СВ.
Начальным моментом n-го порядка являются величины:
− для дискретной СВ
![]() , (5.19)
, (5.19)
− для непрерывной СВ
![]() . (5.20)
. (5.20)
Начальный момент первого порядка (n=1) называется математическим ожиданием:
− для дискретной СВ
![]() , (5.21)
, (5.21)
− для непрерывной СВ
![]() . (5.22)
. (5.22)
Математическое ожидание является средним значением СВ.
Центральным моментом n-го порядка является:
− для дискретной СВ
![]() , (5.23)
, (5.23)
− для непрерывной СВ
![]() . (5.24)
. (5.24)
Центральный момент второго порядка называется дисперсией СВ.
Дисперсия:
− для дискретной СВ
![]() , (5.25)
, (5.25)
− для непрерывной СВ
![]() . (5.26)
. (5.26)
Если случайная величина ![]() физически является электрической величиной, то начальный момент второго порядка представляет собой среднюю мощность СВ, а дисперсия – отклонение мощности от ее среднего значения. Величина
физически является электрической величиной, то начальный момент второго порядка представляет собой среднюю мощность СВ, а дисперсия – отклонение мощности от ее среднего значения. Величина ![]() называется среднеквадратичным отклонением (СКО).
называется среднеквадратичным отклонением (СКО).
В практической радиотехнике наиболее широко используются следующие законы распределения, которые обычно описываются рядом распределения для дискретных СВ и плотностью вероятности – для непрерывных СВ.
Для дискретных СВ
− равномерный закон:
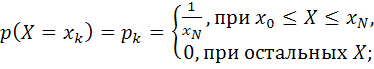 (5.27)
(5.27)
− биномиальный закон определяет вероятность числа k появления случайного события при n независимых испытаниях (например, вероятность появления k единиц в кодовой комбинации из n разрядов):
![]() , (5.28)
, (5.28)
Где ![]() − число сочетаний из n по k,
− число сочетаний из n по k,
p – вероятность появления события (вероятность появления единицы в кодовой комбинации).
Для непрерывных СВ
− равномерный закон
![]() , (5.29)
, (5.29)
где (a,b) – область определения случайной величины;
− нормальный закон
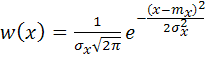 , (5.30)
, (5.30)
где ![]() – математическое ожидание,
– математическое ожидание,
![]() – дисперсия случайной величины.
– дисперсия случайной величины.
Для практических расчетов при решении задач радиотехники используют закон нормально распределенной СВ с нулевым математическим ожиданием ![]() и единичной дисперсией
и единичной дисперсией ![]() . Тогда плотность вероятности
. Тогда плотность вероятности
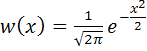 ,
,
а функция распределения
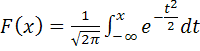 . (5.31)
. (5.31)
Выражение (5.31) называется интегралом вероятности. Его значения рассчитаны и сведены в таблицу, которую можно найти в литературе;
− закон Рэлея определяет распределения модуля вектора на плоскости, составляющие которого по обеим осям независимы и распределены нормально с нулевым математическим ожиданием и дисперсией ![]()
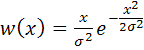 . (5.32)
. (5.32)
Понятия законов распределения можно распространить и на совокупность случайных величин. Так для двух случайных величин ![]() и
и ![]() функцией распределения называется вероятность того, что случайная величина
функцией распределения называется вероятность того, что случайная величина ![]() не превзойдет значения
не превзойдет значения ![]()
![]() . (5.33)
. (5.33)
Очевидно, функция (5.33) является двумерной.
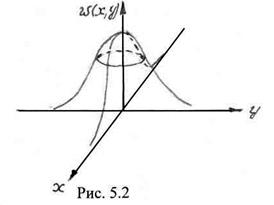
Двумерная плотность распределения двух СВ
![]() . (5.34)
. (5.34)
На рис. 5.2 изображена двумерная плотность ![]() . Так же, как одномерная
. Так же, как одномерная ![]() двумерная плотность неотрицательна
двумерная плотность неотрицательна
![]() .
.
Условие нормировки
![]() . (5.35)
. (5.35)
 Очевидно, из (5.35) вытекает, что объем под поверхностью
Очевидно, из (5.35) вытекает, что объем под поверхностью ![]() равен единице.
равен единице.
По заданной двумерной плотности можно найти одномерные плотности ![]() и
и ![]() . Так
. Так
![]() . (5.36)
. (5.36)
Если случайные величины ![]() и
и ![]() независимы, то
независимы, то
![]() . (5.37)
. (5.37)
При наличии зависимости случайных величин
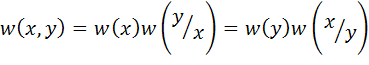 . (5.38)
. (5.38)
Для зависимых случайных величин имеет место коэффициент корреляции
![]() , (5.39)
, (5.39)
характеризующий степень зависимости этих величин.
5.2. Случайные процессы и их вероятностные характеристики
Математическими моделями случайных сигналов и помех являются случайные процессы. Случайным процессом (СП) называется изменение случайной величины во времени. К случайным процессам относится большинство процессов, протекающих в радиотехнических устройствах, а также помехи, сопровождающие передачу сигналов по каналам связи. Случайные процессы могут быть непрерывными (НСП), либо дискретными (ДСП) в зависимости от того, какая случайная величина непрерывная или дискретная изменятся во времени. В дальнейшем основное внимание будет уделено НСП.
 Прежде чем приступить к изучению случайных процессов необходимо определится со способами их представления. Будем обозначать случайный процесс через
Прежде чем приступить к изучению случайных процессов необходимо определится со способами их представления. Будем обозначать случайный процесс через ![]() , а его конкретную реализацию – через
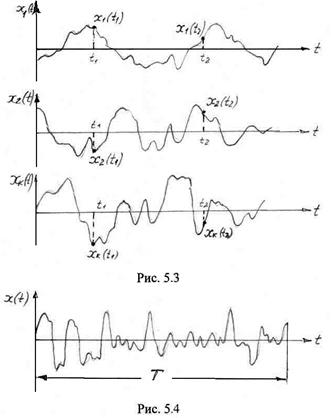
, а его конкретную реализацию – через ![]() . Случайный процесс может быть представлен либо совокупностью (ансамблем) реализаций, либо одной, но достаточно протяженной во времени реализацией. Если сфотографировать несколько осциллограмм случайного процесса и фотографии расположить одну под другой, то совокупность этих фотографий будет представлять ансамбль реализаций (рис. 5.3).
. Случайный процесс может быть представлен либо совокупностью (ансамблем) реализаций, либо одной, но достаточно протяженной во времени реализацией. Если сфотографировать несколько осциллограмм случайного процесса и фотографии расположить одну под другой, то совокупность этих фотографий будет представлять ансамбль реализаций (рис. 5.3).
Здесь ![]() – первая, вторая, …, k-ая реализации процесса. Если же отобразить изменение случайной величины на ленте самописца на достаточно большом интервале времени T, то процесс будет представлен единственной реализацией (рис. 5.3).
– первая, вторая, …, k-ая реализации процесса. Если же отобразить изменение случайной величины на ленте самописца на достаточно большом интервале времени T, то процесс будет представлен единственной реализацией (рис. 5.3).
Как и случайные величины, случайные процессы описываются законами распределения и вероятностными (числовыми) характеристиками. Вероятностные характеристики могут быть получены как усреднение значений случайного процесса по ансамблю реализаций, так и усреднением по одной реализации.
Пусть случайный процесс представлен ансамблем реализаций (рис. 5.3). Если выбрать произвольный момент времени ![]() и зафиксировать значения, принимаемые реализациями
и зафиксировать значения, принимаемые реализациями ![]() в этот момент времени, то совокупность этих значений образует одномерное сечение СП
в этот момент времени, то совокупность этих значений образует одномерное сечение СП
и представляет собой случайную величину ![]() . Как уже подчеркивалось выше, исчерпывающей характеристикой случайной величины
. Как уже подчеркивалось выше, исчерпывающей характеристикой случайной величины ![]() является функция распределения
является функция распределения ![]() или одномерная плотность вероятности
или одномерная плотность вероятности
![]() .
.
Естественно как ![]() , так и
, так и ![]() , обладают всеми свойствами функции распределения и плотности распределения вероятности, рассмотренными выше.
, обладают всеми свойствами функции распределения и плотности распределения вероятности, рассмотренными выше.
Числовые характеристики в сечении ![]() определяются в соответствии с выражениями (5.20), (5.22), (5.24) и (5.26). Так, в частности математическое ожидание СП в сечении
определяются в соответствии с выражениями (5.20), (5.22), (5.24) и (5.26). Так, в частности математическое ожидание СП в сечении ![]() определяется выражением
определяется выражением
![]() , (5.40)
, (5.40)
а дисперсия – выражением
![]() . (5.41)
. (5.41)
Однако, законов распределения и числовых характеристик только в сечении ![]() недостаточно для описания случайного процесса, который развивается во времени. Поэтому, необходимо рассмотреть второе сечении
недостаточно для описания случайного процесса, который развивается во времени. Поэтому, необходимо рассмотреть второе сечении ![]() (рис. 5.3). В этом случае СП будет описываться уже двумя случайными величинами
(рис. 5.3). В этом случае СП будет описываться уже двумя случайными величинами ![]() и
и ![]() , разнесенными между собой на интервал времени
, разнесенными между собой на интервал времени ![]() и характеризоваться двумерной функцией распределения
и характеризоваться двумерной функцией распределения ![]() и двумерной плотностью
и двумерной плотностью ![]() , где
, где ![]() ,
, ![]() . Очевидно, если ввести в рассмотрение третье, четвертое и т.д. сечения, можно прийти к многомерной (N-мерной) функции распределения
. Очевидно, если ввести в рассмотрение третье, четвертое и т.д. сечения, можно прийти к многомерной (N-мерной) функции распределения ![]() и соответственно к многомерной плотности распределения
и соответственно к многомерной плотности распределения ![]() .
.
Важнейшей характеристикой случайного процесса служит автокорреляционная функция (АКФ)
![]() , (5.43)
, (5.43)
устанавливающая степень статистической связи между значениями СП в моменты времени ![]() и
и ![]()
Представление СП в виде ансамбля реализаций приводит к понятию стационарности процесса. Случайный процесс является стационарным, если все начальные и центральные моменты не зависят от времени, т.е.
![]() ,
, ![]() .
.
Это жесткие условия, поэтому при их выполнении СП считается стационаром в узком смысле.
На практике используется понятие стационарности в широком смысле. Случайный процесс стационарен в широком смысле, если его математическое ожидание и дисперсия не зависят от времени, т.е.:
![]() ;
; ![]() , (5.44)
, (5.44)
а автокорреляционная функция определяется только интервалом ![]() и не зависит от выбора
и не зависит от выбора ![]() на оси времени
на оси времени
![]() . (5.45)
. (5.45)
В дальнейшем будут рассматриваться только стационарные в широком смысле случайные процессы.
Выше отмечалось, что случайный процесс помимо представления ансамблем реализаций, может быть представлен единственной реализацией на интервале времени T. Очевидно, все характеристики процесса могут быть получены усреднением значений процесса по времени.
Математическое ожидание СП при усреднении по времени определяется следующим образом:
![]() . (5.46)
. (5.46)
Отсюда следует физический смысл ![]() : математическое ожидание – это среднее значение (постоянная составляющая) процесса.
: математическое ожидание – это среднее значение (постоянная составляющая) процесса.
Дисперсия СП определяется выражением
![]() . (5.47)
. (5.47)
и имеет физический смысл средней мощности переменной составляющей процесса.
Автокорреляционная функция при усреднении по времени
![]() . (5.48)
. (5.48)
Случайный процесс называется эргодическим, если его вероятностные характеристики, полученные усреднением по ансамблю, совпадают с вероятностными характеристиками, полученными усреднением по времени единственной реализации из этого ансамбля. Эргодические процессы являются стационарными.
Использование выражений (5.46), (5.47) и (5.48) требует, строго говоря, реализации случайного процесса большой (теоретически бесконечной) протяженности. При решении практических задач интервал времени ![]() ограничен. При этом большинство процессов считают приблизительно эргодическими и вероятностные характеристики определяют в соответствии с выражениями
ограничен. При этом большинство процессов считают приблизительно эргодическими и вероятностные характеристики определяют в соответствии с выражениями
![]() ; (5.49)
; (5.49)
![]() ;
;
![]() .
.
Случайные процессы, у которых исключено математическое ожидание, называются центрированными. В дальнейшем под ![]() и
и ![]() будут подразумеваться значения центрированных случайных процессов. Тогда выражения для дисперсии и автокорреляционной функции принимают вид
будут подразумеваться значения центрированных случайных процессов. Тогда выражения для дисперсии и автокорреляционной функции принимают вид
![]() ; (5.50)
; (5.50)
![]() . (5.51)
. (5.51)
Отметим свойства АКФ эргодических случайных процессов:
– автокорреляционная функция является вещественной функцией аргумента ![]() ,
,
– автокорреляционная функция является четной функцией, т.е. ![]() ,
,
– при увеличении ![]() АКФ убывает (необязательно монотонно) и при
АКФ убывает (необязательно монотонно) и при ![]() стремится к нулю,
стремится к нулю,
– значение АКФ при ![]() равно дисперсии (средней мощности) процесса
равно дисперсии (средней мощности) процесса
![]() .
.
На практике часто приходится иметь дело с двумя и более СП. Так например, на вход радиоприемника одновременно поступает смесь случайного сигнала и помехи. Взаимную связь между двумя случайными процессами устанавливает взаимная корреляционная функция (ВКФ). Если ![]() и
и ![]() – два случайных процесса, характеризующиеся реализациями
– два случайных процесса, характеризующиеся реализациями ![]() и
и ![]() , то взаимная корреляционная функция определяется выражением
, то взаимная корреляционная функция определяется выражением
![]() . (5.52)
. (5.52)
Взаимная корреляционная функция характеризует степень статистической связи между значениями случайных процессов в моменты времени ![]() и
и ![]() .
.
Часто используют коэффициент взаимной корреляции
![]() , (5.53)
, (5.53)
причем ![]() .
.
Два случайных процесса ![]() и
и ![]() называются некоррелированными если
называются некоррелированными если ![]() .
.
Среди многообразия случайных процессов наиболее широко распространенным является нормальный случайный процесс. Нормальный случайный процесс ![]() в любом сечении его реализации
в любом сечении его реализации ![]() характеризуется плотностью вероятности
характеризуется плотностью вероятности
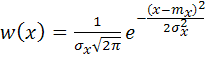 . (5.54)
. (5.54)
Для нормального случайного процесса все числовые характеристики, кроме математического ожидания и дисперсии, равны нулю. Поскольку дисперсия представляет собой значение АКФ при ![]() , то нормальный случайный процесс полностью определяется математическим ожиданием
, то нормальный случайный процесс полностью определяется математическим ожиданием ![]() и автокорреляционной функцией
и автокорреляционной функцией ![]() . Поэтому (5.54) можно представить следующим образом
. Поэтому (5.54) можно представить следующим образом
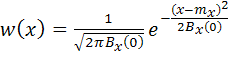 . (5.55)
. (5.55)
Двумерная плотность распределения вероятностей значений ![]() и
и ![]() нормального случайного процесса, разделенных интервалом времени
нормального случайного процесса, разделенных интервалом времени ![]() , имеет вид
, имеет вид
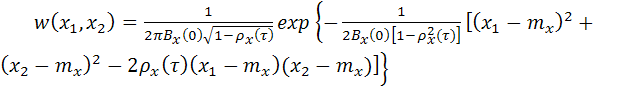 , (5.56)
, (5.56)
где ![]() – нормированная автокорреляционная функция процесса.
– нормированная автокорреляционная функция процесса.
Следует отметить, что для нормального случайного процесса некоррелированность двух значений, разделенных интервалом времени ![]() , означает и их статистическую независимость.
, означает и их статистическую независимость.
5.3. Энергетический спектр случайного процесса
Передача информации в радиотехнических системах связана со спектральными преобразованиями сигналов. Но если спектральные характеристики детерминированных сигналов достаточно просто определяются преобразованием Фурье
![]() ,
,
где ![]() – детерминированная функция, описывающая сигнал,
– детерминированная функция, описывающая сигнал,
![]() – его спектр, т.е. распределение комплексных амплитуд по частоте, то для случайного процесса понятие комплексной амплитуды отсутствует. И тем не менее для случайного процесса можно ввести удобную спектральную характеристику.
– его спектр, т.е. распределение комплексных амплитуд по частоте, то для случайного процесса понятие комплексной амплитуды отсутствует. И тем не менее для случайного процесса можно ввести удобную спектральную характеристику.
Рассмотрим эргодический центрированный случайный процесс. Если выбрать из ансамбля реализаций процесса какую-либо конкретную реализацию ![]() (фотографию процесса) достаточно большой длительности
(фотографию процесса) достаточно большой длительности ![]() (рис. 5.5), то она представляет детерминированную функцию (мы ее наблюдаем и нам известны все изменения случайного процесса). Поэтому к такой реализации можно формально применить преобразование Фурье и вычислить ее спектр
(рис. 5.5), то она представляет детерминированную функцию (мы ее наблюдаем и нам известны все изменения случайного процесса). Поэтому к такой реализации можно формально применить преобразование Фурье и вычислить ее спектр
![]() .
.
Найдем энергию рассматриваемой реализации. Согласно равенству Парсеваля энергия реализации длительностью ![]() равна
равна
![]() . (5.57)
. (5.57)
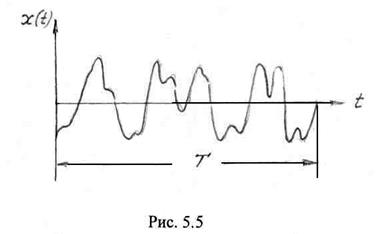 Очевидно, при
Очевидно, при ![]() энергия реализации неограниченно возрастает. Поэтому целесообразно перейти от энергии реализации к средней мощности на интервале
энергия реализации неограниченно возрастает. Поэтому целесообразно перейти от энергии реализации к средней мощности на интервале ![]() . Для этого разделим обе части равенства (5.57) на
. Для этого разделим обе части равенства (5.57) на ![]()
![]() . (5.58)
. (5.58)
Отношение ![]() представляет собой спектральную плотность средней мощности, т.е. среднюю мощность, приходящуюся на единицу полосы частот и имеет размерность
представляет собой спектральную плотность средней мощности, т.е. среднюю мощность, приходящуюся на единицу полосы частот и имеет размерность ![]() .
.
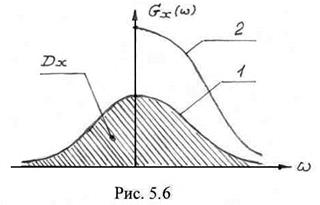 Функция
Функция
![]() , (5.59)
, (5.59)
характеризует энергетический спектр, т.е. распределение средней мощности по частоте. На рис. 5.6 изображен энергетический спектр случайного процесса. Отметим некоторые свойства функции энергетического спектра:
– энергетический спектр ![]() является вещественной неотрицательной функцией частоты
является вещественной неотрицательной функцией частоты ![]() ;
;
– энергетический спектр является четной функцией частоты, т.е. ![]() (кривая 1 на рис. 5.5). На этом основании часто используют функцию
(кривая 1 на рис. 5.5). На этом основании часто используют функцию
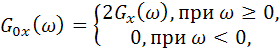
называемую односторонним энергетическим спектром (кривая 2 на рис. 5.6).
Так как мы рассматриваем центрированный случайный процесс, т.е. процесс у которого исключено математическое ожидание (постоянная составляющая), очевидно средняя мощность любой его реализации равна дисперсии процесса. Тогда можно записать
![]() . (5.60)
. (5.60)
Иными словами, дисперсия процесса равно площади под кривой ![]() .
.
В заключение отметим, что в технических расчетах вместо ![]() часто используют энергетический спектр
часто используют энергетический спектр ![]() как функцию циклической частоты
как функцию циклической частоты ![]()
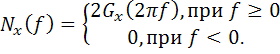 (5.61)
(5.61)
5.4. Теорема Винера–Хинчина
Энергетический спектр и автокорреляционная функция случайного процесса являются неслучайными функциями, связанными между собой. Установим эту связь. Рассмотрим реализацию ![]() случайного процесса длительностью
случайного процесса длительностью ![]() и ее копию
и ее копию ![]() , сдвинутую на интервал времени
, сдвинутую на интервал времени ![]() . Известно, что энергетический спектр и автокорреляционная функция детерминированного сигнала связаны между собой парой преобразований Фурье. Тогда с учетом выше приведенного предположения о том, что реализация
. Известно, что энергетический спектр и автокорреляционная функция детерминированного сигнала связаны между собой парой преобразований Фурье. Тогда с учетом выше приведенного предположения о том, что реализация ![]() и ее копия
и ее копия ![]() нам известны, можно записать
нам известны, можно записать
![]() .
.
Разделим обе части этого равенства на ![]()
![]() , (5.62)
, (5.62)
и устремим ![]() .
.
Тогда в соответствии с (5.51) левая часть равенства (5.62) представляет собой автокорреляционную функцию ![]() . Учитывая (5.59) равенство (5.62) можно представить следующим образом
. Учитывая (5.59) равенство (5.62) можно представить следующим образом
![]() . (5.63)
. (5.63)
Но это есть обратное преобразование Фурье, связывающее АКФ случайного процесса с его энергетическим спектром. Очевидно, если существует обратное преобразование, значит, существует и прямое преобразование Фурье
![]() , (5.64)
, (5.64)
связывающее энергетический спектр с АКФ.
Таким образом, АКФ случайного процесса и его энергетический спектр связаны между собой парой преобразований Фурье. Впервые эта связь была установлена советским математиком А. Хинчиным и независимо от него американским ученым Н. Винером. Поэтому соотношения (5.63) и (5.64) носят название теоремы Винера–Хинчина.
Так как автокорреляционная функция ![]() и энергетический спектр
и энергетический спектр ![]() являются вещественными четными функциями, можно отказаться от комплексной формы записи преобразования Фурье и перейти к другой форме
являются вещественными четными функциями, можно отказаться от комплексной формы записи преобразования Фурье и перейти к другой форме
![]() , (5.65)
, (5.65)
![]() . (5.66)
. (5.66)
Из этих выражений следует
![]() , (5.67)
, (5.67)
![]() . (5.68)
. (5.68)
Но ![]() , откуда
, откуда
![]() ,
,
что совпадает с (5.60).
В случае, когда энергетический спектр описывается функцией циклической частоты (5.61), выражения (5.65) – (5.68) приобретают вид
![]() , (5.69)
, (5.69)
![]() . (5.70)
. (5.70)
![]() , (5.71)
, (5.71)
![]() . (5.72)
. (5.72)
5.5. Эффективная ширина спектра и интервал корреляции
При спектральных преобразованиях случайных процессов важное значение приобретает ширина спектра процесса. Эффективная ширина энергетического спектра определяется следующим образом:
![]() , (5.73)
, (5.73)
или
![]() . (5.74)
. (5.74)
Этому определению можно дать графическую интерпретацию. На рис. 5.7 изображена кривая одностороннего энергетического спектра. Построим прямоугольник с площадью, равной площади по кривой ![]() , одна сторона которого составляет величину
, одна сторона которого составляет величину ![]() (в данном случае
(в данном случае ![]() ). Тогда вторая сторона прямоугольника будет характеризовать эффективную ширину энергетического
). Тогда вторая сторона прямоугольника будет характеризовать эффективную ширину энергетического 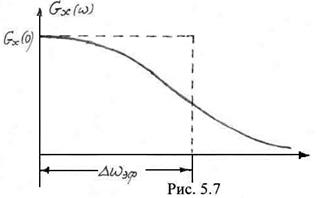 спектра
спектра ![]() . Представим выражение (5.71) в следующем виде
. Представим выражение (5.71) в следующем виде
![]() .
.
Левая сторона этого равенства представляет собой среднюю мощность случайного процесса с равномерным энергетическим спектром в пределах полосы частот ![]() , а правая – среднюю мощность рассматриваемого случайного процесса.
, а правая – среднюю мощность рассматриваемого случайного процесса.
Тогда эффективную ширину спектра рассматриваемого случайного процесса можно трактовать как ширину спектра процесса с равномерной плотностью мощности при равенстве средних мощностей обоих процессов.
Как подчеркивалось выше, автокорреляционная функция случайного процесса характеризует степень статистической связи между значениями процесса, разделенными интервалом времени ![]() . При этом, для эргодических процессов, которые изучаются в радиотехнике, АКФ стремится к нулю при неограниченном возрастании
. При этом, для эргодических процессов, которые изучаются в радиотехнике, АКФ стремится к нулю при неограниченном возрастании ![]() . Очевидно, при определенном значении
. Очевидно, при определенном значении ![]() , значения случайного процесса
, значения случайного процесса ![]() и
и ![]() можно считать статистически несвязанными (некоррелированными). Значение
можно считать статистически несвязанными (некоррелированными). Значение ![]() , при котором значения случайного процесса
, при котором значения случайного процесса ![]() и
и ![]() становятся статистически несвязанными, называется интервалом корреляции.
становятся статистически несвязанными, называется интервалом корреляции.
Интервал корреляции определяется в соответствии с выражением
![]() , (5.75)
, (5.75)
где ![]() – нормированная автокорреляционная функция.
– нормированная автокорреляционная функция.
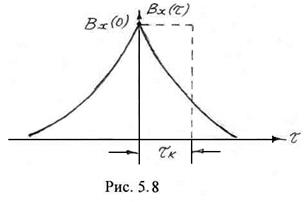
Знак модуля в (5.75) введен для случая, когда ![]() может принимать отрицательные значения. На рис. 5.8 приведена графическая интерпретация понятия интервала корреляции. Интервал корреляции представляет собой сторону прямоугольника, по площади равному площади под кривой
может принимать отрицательные значения. На рис. 5.8 приведена графическая интерпретация понятия интервала корреляции. Интервал корреляции представляет собой сторону прямоугольника, по площади равному площади под кривой ![]() при
при ![]() .
.
 Установим связь между эффективной шириной спектра и интервалом корреляции в предположении, что
Установим связь между эффективной шириной спектра и интервалом корреляции в предположении, что ![]() , а функция корреляции представляет собой неотрицательную монотонно убывающую функцию, что позволяет в (5.75) полагать
, а функция корреляции представляет собой неотрицательную монотонно убывающую функцию, что позволяет в (5.75) полагать ![]() . Найдем произведение
. Найдем произведение ![]() и
и ![]() с учетом (5.73) и (5.75).
с учетом (5.73) и (5.75).
![]() .
.
Подставляя в это выражение формулы (5.67) и (5.68) после несложных преобразований получим
![]() . (5.76)
. (5.76)
Аналогично, используя выражения (5.71), (5.72), (5.74) и (5.75), можно получить
![]() . (5.77)
. (5.77)
Таким образом, произведение эффективной ширины спектра и интервала корреляции представляет собой постоянную величину. Из этого вытекает, что чем шире энергетический спектр, тем меньше интервал корреляции между его значениями и наоборот. Но ширина энергетического спектра определяет скорость изменения значений случайного процесса: чем больше ![]() (или чем меньше
(или чем меньше ![]() ), тем выше скорость изменения процесса.
), тем выше скорость изменения процесса.
5.6. Белый шум и его характеристики
Особое место при анализе процессов, протекающих в радиотехнических и информационных системах, занимает нормальный случайный процесс с нулевым математическим ожиданием и автокорреляционной функцией:
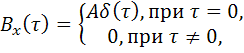 (5.78)
(5.78)
где ![]() – дельта функция.
– дельта функция.
Такой случайный процесс получил название «белого шума». Значения «белого шума» при сколь угодно малом значении ![]() некоррелированы. При этом, как следует из (5.78)
некоррелированы. При этом, как следует из (5.78)
![]() ,
,
т.е. средняя мощность белого шума неограниченна.
«Белый шум» является математической абстракцией, которая, тем не менее, существенно упрощает анализ процессов в радиотехнических системах. В природе процессов вида «белого шума» не существует, но при определенных предположениях реальные помехи можно описать моделью «белого шума».
Найдем значение коэффициента ![]() в (5.78). Для этого подставим (5.78) в (5.68).
в (5.78). Для этого подставим (5.78) в (5.68).
![]() .
.
Используя фильтрующее свойство дельта-функции при ![]() , получим
, получим
![]() . (5.79)
. (5.79)
Отсюда следует, что «белый шум» имеет равномерный энергетический спектр в диапазоне частот от 0 до ∞ со спектральной плотностью мощности ![]() . Выражая
. Выражая ![]() через
через ![]() из (5.79) и подставляя его в (5.78), получим
из (5.79) и подставляя его в (5.78), получим
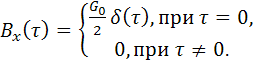 (5.80)
(5.80)
Аналогичными рассуждениями при использовании выражения (5.69) можно получить
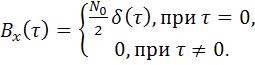 (5.81)
(5.81)
Выражение (5.81) наиболее часто используется при решении различных задач радиотехники. Свое название «белый шум» получил по аналогии со световым потоком, отраженным от листа белой бумаги. Такой поток имеет равномерный спектр в очень широком диапазоне частот.
Ввиду того, что автокорреляционная функция «белого шума» представляет собой дельта-функцию, «белый шум» часто называют дельта-коррелированным случайным процессом. Отсутствие корреляции между любыми, сколь угодно близкими значениями «белого шума» означает бесконечно большую скорость изменения процесса.
В радиотехнических задачах моделью «белого шума», в частности описываются тепловые и дробовые шумы элементов радиотехнических устройств.
Тепловые шумы резисторов возникают из-за хаотического теплового движения заряда в проводящих элементах. Внутри объема резистора возникают электромагнитные поля и на внешних зажимах появляется шумовая разность потенциалов. Энергетический спектр шума оказывается очень широким из-за высокой скорости теплового движения электронов и описывается выражением
![]() , (5.82)
, (5.82)
где ![]() – постоянная Больцмана,
– постоянная Больцмана,
![]() – абсолютная температура (в градусах по Кельвину),
– абсолютная температура (в градусах по Кельвину),
![]() – значение сопротивления резистора.
– значение сопротивления резистора.
Из (5.82) следует, что снизить интенсивность ![]() теплового шума можно уменьшая
теплового шума можно уменьшая ![]() . Вот почему в радиолокации, радиоастрономии и космической связи применяют глубокое охлаждение входных цепей радиоприемных устройств.
. Вот почему в радиолокации, радиоастрономии и космической связи применяют глубокое охлаждение входных цепей радиоприемных устройств.
Дробовой шум возникает в электронных приборах (лампах, транзисторах и т.д.). Природу дробового шума можно пояснить на примере вакуумного диода, в котором электроны эмитируются из катода и затем перемещаются к аноду под действием электрического поля. Ток, создаваемый потоком электронов, представляет собой сумму коротких импульсов тока, обусловленных перемещением электронов от катода к аноду. Хотя время пролета электрона от катода к аноду составляет величину порядка ![]() , за счет случайности моментов вылета электронов с поверхности катода суммарный ток носит случайный характер. Энергетический спектр дробового шума также является равномерным в очень широком диапазоне частот за счет малой длительности каждого из импульсов, образующих дробовой шум. Для оценки энергетического спектра дробового шума используется выражение
, за счет случайности моментов вылета электронов с поверхности катода суммарный ток носит случайный характер. Энергетический спектр дробового шума также является равномерным в очень широком диапазоне частот за счет малой длительности каждого из импульсов, образующих дробовой шум. Для оценки энергетического спектра дробового шума используется выражение
![]() , (5.83)
, (5.83)
где ![]() – средние значение тока,
– средние значение тока,
![]() – среднее число электронов, достигающих анода за единицу времени,
– среднее число электронов, достигающих анода за единицу времени,
![]() – электрический заряд, переносимый каждым электроном.
– электрический заряд, переносимый каждым электроном.
Соотношение (5.83) получило название формулы Шоттки.
5.7. Узкополосный случайный процесс
Случайный процесс, энергетический спектр которого сосредоточен в относительно узкой полосе частот вблизи некоторой частоты ![]() , называется узкополосным процессом. Узкополосный СП имеет место, например, на выходе резонансного усилителя при подаче на его вход широкополосного случайного процесса вида «белого шума». Так как спектр такого СП сосредоточен вокруг частоты
, называется узкополосным процессом. Узкополосный СП имеет место, например, на выходе резонансного усилителя при подаче на его вход широкополосного случайного процесса вида «белого шума». Так как спектр такого СП сосредоточен вокруг частоты ![]() его можно представить в виде квазигармонического (почти гармонического) колебания
его можно представить в виде квазигармонического (почти гармонического) колебания
![]() , (5.84)
, (5.84)
где ![]() и
и ![]() – соответственно огибающая и начальная фаза, которые являются случайными медленно меняющимися (по сравнению с
– соответственно огибающая и начальная фаза, которые являются случайными медленно меняющимися (по сравнению с ![]() ) функциями.
) функциями.
Воспользовавшись известным тригонометрическим соотношением
![]() ,
,
представим (5.84) в виде
![]()
или
![]() , (5.85)
, (5.85)
где ![]() ;
;
![]() . (5.86)
. (5.86)
В свою очередь ![]() ;
;
![]() . (5.87)
. (5.87)
Для определения статистических характеристик огибающей и фазы удобно представить узкополосный случайный процесс в комплексной форме
![]() . (5.88)
. (5.88)
Вещественная часть
![]() (5.89)
(5.89)
и мнимая часть
![]() (5.90)
(5.90)
являются комплексно-сопряженными процессами, связанными между собой преобразованиями Гильберта
![]() ;
; ![]() .
.
Напомним, что сигнал ![]() , сопряженный с
, сопряженный с ![]() получается при повороте фаз всех гармонических составляющих
получается при повороте фаз всех гармонических составляющих ![]() на угол
на угол ![]() .
.
Теперь с учетом (5.89) и (5.90) выражение (5.88) можно представить следующим образом
![]() . (5.91)
. (5.91)
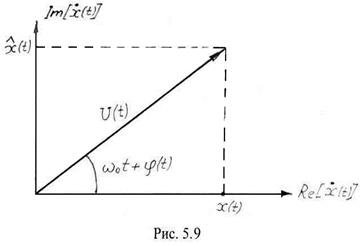
Графически комплексный случайный процесс изображается на комплексной плоскости вектором ![]() случайной длины и случайным фазовым углом
случайной длины и случайным фазовым углом ![]() , который вращается с частотой
, который вращается с частотой ![]() ротив часовой стрелки (рис. 5.9). в момент времени
ротив часовой стрелки (рис. 5.9). в момент времени ![]() этот вектор образует с вещественной осью полный угол
этот вектор образует с вещественной осью полный угол ![]() .
.
 Приведем некоторые соотношения, характеризующие
Приведем некоторые соотношения, характеризующие ![]() и
и ![]() . В первую очередь отметим, что энергетические спектры
. В первую очередь отметим, что энергетические спектры ![]() и
и ![]() одинаковы, т.е.
одинаковы, т.е.
![]() . (5.92)
. (5.92)
Если энергетические спектры одинаковы, то в соответствии с теоремой
Винера–Хинчина одинаковыми будут и автокорреляционные функции
![]() . (5.93)
. (5.93)
Функция взаимной корреляции при ![]()
![]() , (5.94)
, (5.94)
т.е. в совпадающие моменты времени значения ![]() и
и ![]() не коррелированны.
не коррелированны.
5.8. Вероятностные характеристики огибающей и начальной фазы узкополосного СП
Во многих радиотехнических задачах возникает необходимость учета случайного характера огибающих и начальных фаз узкополосных случайных процессов. При этом в качестве узкополосного процесса чаще всего выступает нормальный случайный процесс. Поэтому в дальнейшем мы остановимся на изучении такого вида процессов.
Итак, пусть ![]() – узкополосный случайный процесс, мгновенные значения которого распределены по нормальному закону с нулевым математическим ожиданием
– узкополосный случайный процесс, мгновенные значения которого распределены по нормальному закону с нулевым математическим ожиданием ![]()
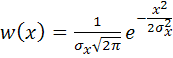 .
.
Этому процессу соответствует комплексный случайный процесс
![]() ,
,
причем комплексно-сопряженный процесс также распределен по нормальному закону с нулевым математическим ожиданием и той же дисперсией, т.е. ![]()
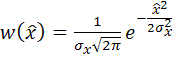 .
.
Так как значения ![]() и
и ![]() некоррелированы, а для нормальных случайных процессов некоррелированность означает и статистическую независимость, то это значит, что двумерная плотность вероятности
некоррелированы, а для нормальных случайных процессов некоррелированность означает и статистическую независимость, то это значит, что двумерная плотность вероятности
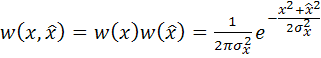 . (5.95)
. (5.95)
Для определения законов распределения огибающей и начальной фазы необходимо перейти от декартовой ![]() к полярной
к полярной ![]() системе координат (рис. 5.10) связь между двумя координатными
системе координат (рис. 5.10) связь между двумя координатными 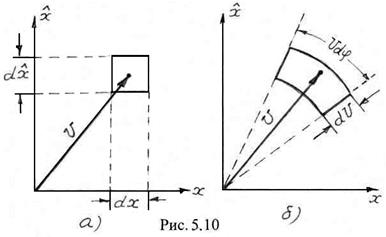 системами определяется следующими соотношениями:
системами определяется следующими соотношениями:
![]() ;
; ![]() . (5.96)
. (5.96)
Выделим бесконечно малую область ![]() в окрестности конца вектора
в окрестности конца вектора ![]() в декартовой системе координат (рис. 5.10а). Очевидно, площадь этой области будет равна
в декартовой системе координат (рис. 5.10а). Очевидно, площадь этой области будет равна ![]() , а вероятность попадания конца вектора
, а вероятность попадания конца вектора ![]() в эту область
в эту область
![]() . (5.97)
. (5.97)
При переходе к полярной системе координат область ![]() трансформируется в область
трансформируется в область ![]() (рис. 5.10б). Вероятность попадания конца вектора
(рис. 5.10б). Вероятность попадания конца вектора ![]() в эту область будет равна:
в эту область будет равна:
![]() . (5.98)
. (5.98)
Так как при переходе из одной системы координат в другую вероятности попадания конца вектора ![]() в элементарные области должны
в элементарные области должны
быть равны, приравняем правые части (5.97) и (5.98)
![]() . (5.99)
. (5.99)
Подстановка (5.95) и (5.96) в (5.99) с учетом того, что ![]() ;
; ![]() после несложных преобразований дает
после несложных преобразований дает
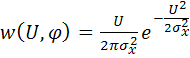 . (5.100)
. (5.100)
Выражение (5.100) представляет собой двумерную плотность распределения значений огибающей и начальной фазы узкополосного СП.
Для того, чтобы найти одномерную плотность распределения огибающей необходимо (5.100) проинтегрировать по всем значениям фазы от ![]() до
до ![]()
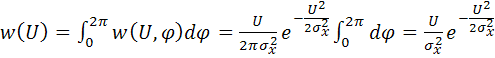 . (5.101)
. (5.101)
Таким образом, значения огибающей узкополосного СП распределены по закону Рэлея.
Аналогично для определения одномерной плотности распределения значений начальной фазы проинтегрируем (5.100) по всем значениям ![]() от
от ![]() до
до ![]()
![]() .
.
Подстановка в это выражение формулы (5.100) с учетом того, что
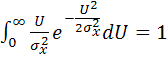 ,
,
(условие нормировки), дает:
![]() . (5.102)
. (5.102)
Отсюда следует, что значения фазы узкополосного СП распределены по равномерному закону в пределах от ![]() до
до ![]() .
.
Рассмотри случай, когда случайный процесс представляет сумму узкополосного детерминированного сигнала
![]() ,
,
и случайного процесса (5.84). Представляя суммарный процесс в комплексной форме и проводя аналогичные рассуждения, можно получить выражение для одномерной плотности вероятности огибающей
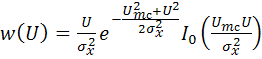 , (5.103)
, (5.103)
где ![]() – модифицированная функция Бесселя нулевого порядка.
– модифицированная функция Бесселя нулевого порядка.
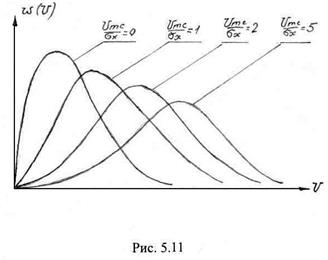 Выражение (5.103) представляет собой обобщенный закон Рэлея или закон Райса. На рис. 5.11 представлены кривые плотности вероятности огибающей суммарного процесса. Из рисунка следует, что форма кривой
Выражение (5.103) представляет собой обобщенный закон Рэлея или закон Райса. На рис. 5.11 представлены кривые плотности вероятности огибающей суммарного процесса. Из рисунка следует, что форма кривой ![]() и ее положение зависит от отношения
и ее положение зависит от отношения ![]() , т.е. от отношения амплитуды сигнала к средне-квадратичному значению шума, в качестве которого здесь выступает процесс (5.84). При
, т.е. от отношения амплитуды сигнала к средне-квадратичному значению шума, в качестве которого здесь выступает процесс (5.84). При ![]() кривая закона Райса приближается к нормальному закону.
кривая закона Райса приближается к нормальному закону.
5.9. Дискретные случайные процессы
В связи с развитием систем передачи цифровых сообщений возникла необходимость изучения дискретных случайных процессов. Ниже будут рассмотрены два вида таких процессов, а именно случайный и синхронный телеграфные сигналы.
Случайным телеграфным сигналом называют процесс, реализации которого принимают значения ![]() и
и ![]() , причем смены знака происходят в случайные моменты времени. Такой процесс наблюдается на выходе усилителя – ограничителя с порогами ограничения
, причем смены знака происходят в случайные моменты времени. Такой процесс наблюдается на выходе усилителя – ограничителя с порогами ограничения ![]() и
и ![]() при поступлении на его вход нормального случайного процесса.
при поступлении на его вход нормального случайного процесса.
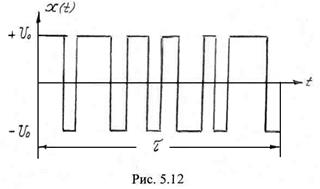 На рис. 5.12 изображена реализация случайного телеграфного сигнала. Для случайного телеграфного сигнала число
На рис. 5.12 изображена реализация случайного телеграфного сигнала. Для случайного телеграфного сигнала число ![]() смены знака за время
смены знака за время ![]() представляет собой дискретную случайную величину, распределенную по закону Пуассона
представляет собой дискретную случайную величину, распределенную по закону Пуассона
![]() , (5.104)
, (5.104)
где ![]() – интенсивность, т.е. число смены знака за единицу времени.
– интенсивность, т.е. число смены знака за единицу времени.
Найдем автокорреляционную функцию и энергетический спектр случайного телеграфного сигнала. В первую очередь отметим, что математическое ожидание случайного телеграфного сигнала ![]() . Автокорреляционная функция определяется усреднением произведения
. Автокорреляционная функция определяется усреднением произведения ![]() , т.е.
, т.е.
![]() ,
,
где черта означает операцию усреднения.
Это произведение принимает значение либо ![]() , если число смены знаков за время
, если число смены знаков за время ![]() будет четным, либо
будет четным, либо ![]() , если число смены знаков будет нечетным. Так как вероятность числа смены знаков определяется законом Пуассона, то
, если число смены знаков будет нечетным. Так как вероятность числа смены знаков определяется законом Пуассона, то
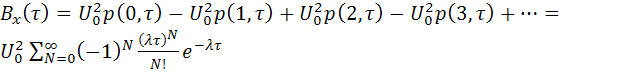 .
.
Сумма сходящегося бесконечного ряда
![]() .
.
Отсюда АКФ случайного телеграфного сигнала
![]() , при
, при ![]() .
.
С учетом того, что ![]() можно окончательно записать
можно окончательно записать
![]() . (5.105)
. (5.105)
Односторонний энергетический спектр вычисляется в соответствии с теоремой Винера–Хинчина
![]() .
.
Подстановка в это выражение соотношения (5.105) при ![]() , дает
, дает
![]() . (5.106)
. (5.106)
При вычислении (5.106) был использован табличный интеграл:
![]() .
.
Синхронный телеграфный сигнал характеризуется тем, что смена знака сигнала происходит в строго определенные моменты времени, кратные длительности импульса τи. На рис. 5.13 изображена 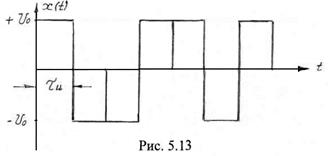
реализация синхронного телеграфного сигнала. Таким образом, синхронный телеграфный сигнал представляет собой случайную последовательность разнополярных прямоугольных импульсов длительностью ![]() .
.
Автокорреляционная функция синхронного телеграфного сигнала описывается выражением
![]() , (5.107)
, (5.107)
а энергетический спектр, вычисленный в соответствии с теоремой Винера–Хинчина
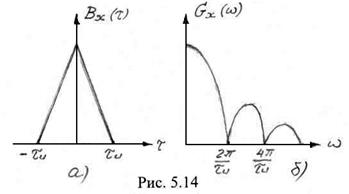
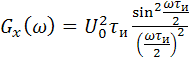 . (5.108)
. (5.108)
На рис. 5.14 изображены автокорреляционная функция и энергетический спектр синхронного телеграфного сигнала. Здесь прослеживается аналогия характеристик синхронного телеграфного сигнала и периодической последовательности разнополярных импульсов (последовательность вида «меандр»). Вместе с тем, если автокорреляционная функция периодической последовательности тоже периодична, то у синхронного телеграфного сигнала это свойство отсутствует.
В заключении отметим, что моделью синхронного телеграфного сигнала может быть описана последовательность кодовых комбинаций при передаче цифровых сигналов.

