При цифровой обработке для повышения скорости обычно используют дискретное преобразование Фурье. Для частотного представления сигнала требуется большое количество операций умножения.

В 1965г изобретено быстрое преобразование Фурье, существенно уменьшающее количество операций умножения.

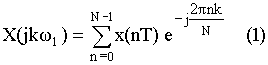прямое преобразование Фурье.

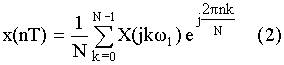обратноe преобразование Фурье.

При прямом преобразовании Фурье:

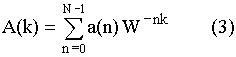; где

При обратном преобразовании Фурье:

Для вывода БПФ заменим прямое и обратное преобразование Фурье формулой (3), где:

a(n) – сигналы отсчета во временной области,

A(k) – отсчеты в частотной области исследуемого сигнала.

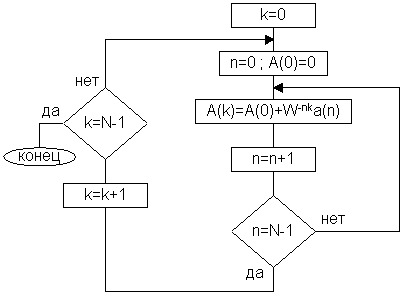
Проанализируем общий алгоритм вычисления ДПФ и обратного ДПФ.

Q_общ – операции умножения

Q_общ = N²

При вычислении весов функции , много значений этой функции дублируется, а именно, при вычислении N точечного вычисления ДПФ, значений W оказываются лишними. Проанализируем поведение весов. функции для N=8.

N=8 W⁰ = 1

При анализе поведения весовой функции видна следующая закономерность: значений весовой функции (первые значения равны следующим весовой функции, взятых со знаком “–”).

nk	0	1	2	3	4	5	6	7
W-nk	1	W-1	W-2	W-3	-1	-W-1	-W-2	-W-3

Используем свойство весовой функции для уменьшения операций умножения. Для этого разобьем последовательность прямого преобразования Фурье на четные и нечетные составляющие.

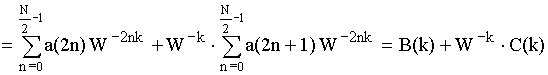
Для получения восьмиточечного ДПФ, исходя из ниже следующей формулы, воспользуемся следующей структурой:

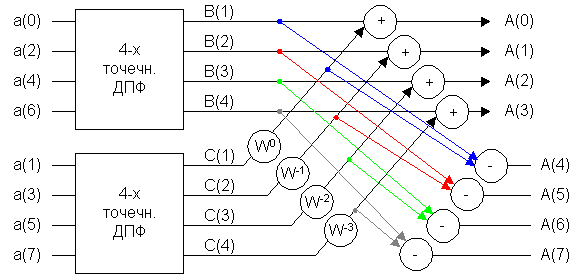
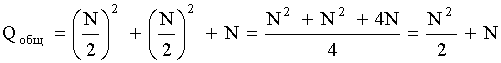
Исходя из преобразования 4-х точечного ДПФ, сделаем преобразование до 2-х точечного ДПФ. Тогда структура будет следующая:

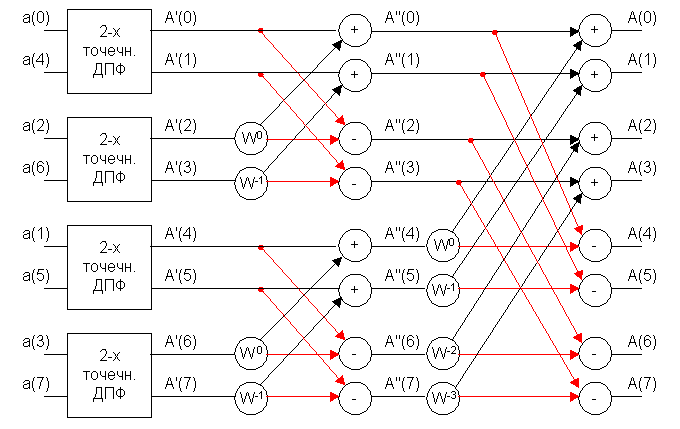
При преобразовании 8-ми точечного ДПФ в 2-х точечное существенно сокращается количество умножений. Первая стадия преобразования 2-х точечного ДПФ вырождается в структуру:

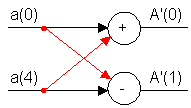
Структура БПФ предполагает замену операции умножения на операцию суммирования или вычитания. При выполнении операции суммирования или вычитания требуется существенно меньше времени, чем для операции умножения.

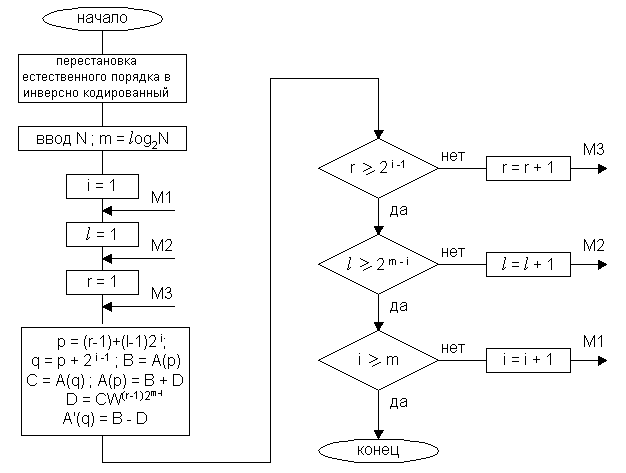
Для реализации БПФ отсчеты подлежащие преобразованию должны подаваться в инверсно–кодированной форме.

“n”текущ.	000	001	010	011	100	101	110	111
БПФ	000	100	010	110	001	101	011	111

При представлении сигнала в инверсно–кодированной форме, получаем эквивалентный зеркальный переворот значений разрядов. Там, где отсчеты располагаются симметрично, никакого преобразования не надо.

При инверсно–кодированных операциях необходимо зеркально отобразить исходную последовательность номеров. Реализация с помощью аппаратных средств производит перекодирование в двоично-инверсную последовательность.

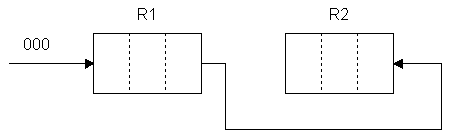
N0такта	P1	P2	P3	N0такта	P1	P2	P3
1	0			4			¬0
2	0	0		5		0	0
3	0	0	0	6	0	0	0

На вход регистра R1 подавалась кодовая комбинация из трех нулей. После шести тактов в регистре R2 будет также последовательность состоящая из трех нулей.

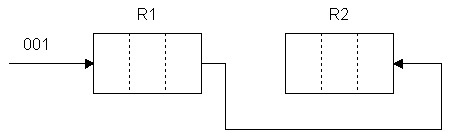
N0такта	P1	P2	P3	N0такта	P1	P2	P3
1	1			4			1
2	0	1		5		1	0
3	0	0	1	6	1	0	0

Если кодовые комбинации не симметричны (1, 4, 6), то они подлежат преобразованию в двоично-инверсную кодированную форму.

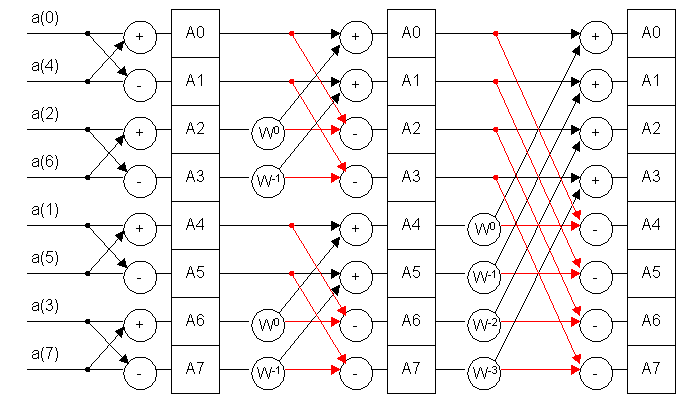
Реализация алгоритма БПФ.

После каждого этапа преобразования получается массив, который обозначается А0 – А7. Так как результаты предыдущих вычислений в дальнейших расчетах используются один раз, то вместо прежних значений А0 – А7 рассчитываются новые значения А0 – А7, таким образом уменьшается объем памяти.

На каждом этапе количество N изменяется. Чтобы упростить вычисление и сделать алгоритм общим, для всех этапов полагают N равно исходному значению отсчетов, которые подлежат преобразованию.

Пример:

С помощью БПФ рассчитать спектральный состав временной последовательности представленной в виде:

x(nT) = {1; 1; -1; -1; 1; 1; -1; -1}

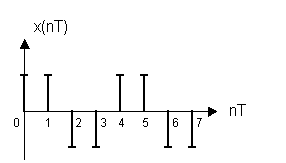
X(jkω₁) = {0; 0; 4 – 4j; 0; 0; 0; 4 + 4j; ? ; 0 }

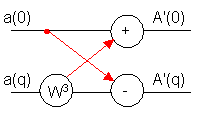
r – количество пар ()

m – количество этапов преобразования

r – текущее значение вычисляемой пары