8.1. Дискретизация аналоговых сигналов. Спектр дискретного сигнала

8.2. Дискретное преобразование Фурье

8.3. Быстрое преобразование Фурье

8.4. Общее описание дискретной цепи. Линейное разностное уравнение

8.5. Основные характеристики дискретной линейной цепи

8.6. Z-преобразование и системная функция дискретной цепи

8.7. Цифровые фильтры

8.8. Методы синтеза цифровых фильтров

8.1. Дискретизация аналоговых сигналов. Спектр дискретного сигнала

В настоящее время в связи с широким распространением цифровых систем передачи и обработки информации возникла необходимость изучения принципов формирования и методов оценки характеристик таких сигналов. Как известно из предыдущего материала, формирование цифрового сигнала включает в себя следующие операции: дискретизацию аналогового сигнала во времени, квантование дискретного сигнала по уровню и перекодирование значений квантованного сигнала из одной системы счисления в другую (в подавляющем большинстве случаев – в двоичную). Мы начнем с рассмотрения спектральных характеристик дискретного сигнала.

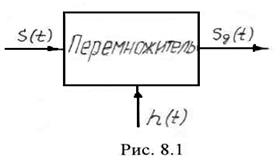Напомним, что дискретный сигнал (или дискретная последовательность) формируется при помощи перемножителя (рис. 8.1), на один из входов которого поступает аналоговый сигнал , а на второй – последовательность коротких импульсов с периодом следования , значение которого определяется теоремой Котельникова

,

где или – верхняя граничная частота аналогового сигнала .

Тогда дискретный сигнал может быть описан выражением

. (8.1)

Вычислим спектр дискретного сигнала. В первую очередь, рассмотрим второй сомножитель выражения (8.1)

. (8.2)

Этот сомножитель представляет собой математическое описание периодической последовательности импульсов. Обычно при осуществлении операции дискретизации форма импульса выбирается прямоугольной. Поэтому в дальнейшем будем полагать, что представляет собой периодическую последовательность прямоугольных импульсов амплитудой и длительностью , следующих с периодом .

Как известно, периодическая последовательность прямоугольных импульсов может быть представлена рядом Фурье, который для рассматриваемого случая принимает вид

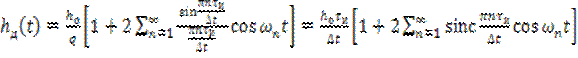. (8.3)

где , – скважность, .

Тогда с учетом (8.3) выражение (8.1) принимает вид

. (8.4)

Применим к (8.4) прямое преобразование Фурье

.

Подстановка в эту формулу выражения (8.4) дает

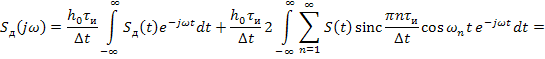
. (8.5)

Интеграл первого слагаемого в (8.5) представляет собой спектр исходного аналогового сигнала. Представим второе слагаемое в (8.5) в виде

. (8.6)

Учитывая, что , запишем

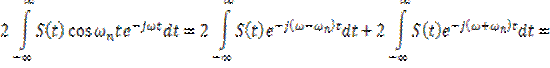
. (8.7)

Тогда с учетом (8.6) и (8.7) выражение (8.5) принимает вид

. (8.8)

Здесь пределы суммирования составляют в виду того, что спектр распространяется на область отрицательных частот.

Дальнейший спектральный анализ дискретного сигнала существенно упрощается, если предположить, что дискретизация осуществляется последовательностью прямоугольных импульсов единичной площади. В этом случае амплитуда импульса и выражение (8.8) запишется следующим образом

. (8.9)

Если устремить , т.е. перейти к последовательности бесконечно коротких импульсов ( -импульсов), т.е.

, (8.10)

то с учетом того, что , спектральная функция дискретного сигнала окончательно принимает вид

. (8.11)

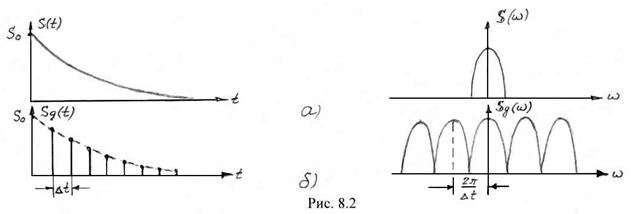
На рис. 8.2 а) представлен аналоговый сигнал и условное изображение модуля его спектральной функции , а на рис. 8.2б – дискретный сигнал и модуль его спектра . Из выражения (8.11) и рис. 8.2 следует, что спектр дискретного сигнала представляет собой бесконечную последовательность копий спектра исходного аналогового сигнала , причем эта последовательность носит периодический характер. Расстояние по оси частот между отдельными копиями составляет (или ), что соответствует периоду последовательности копий на оси частот. Отметим, что (или ) – это частота дискретизации. Таким образом, период спектральной функции дискретного сигнала равен частоте дискретизации.

8.2. Дискретное преобразование Фурье

Модель дискретного сигнала вида (8.10) предполагает, что отсчетные значения аналогового (непрерывного) сигнала берутся на неограниченном интервале времени. Однако, на практике осуществить такую дискретизацию невозможно, т.е. реальные сигналы ограничены во времени и дискретизация проводится на конечном интервале времени, равном длительности сигнала .

Рассмотрим особенности спектрального представления дискретного сигнала, который задан на интервале своими отсчетами , взятыми соответственно в моменты времени . Очевидно, что полное число отсчетов равно .

При спектральном анализе дискретных сигналов ограниченной длительности полагают, что такой сигнал периодически повторяется, с периодом равным (рис. 8.3а). А это означает, что такой периодический сигнал может быть представлен рядом Фурье (тригонометрическим или комплексным). Поскольку спектр периодического дис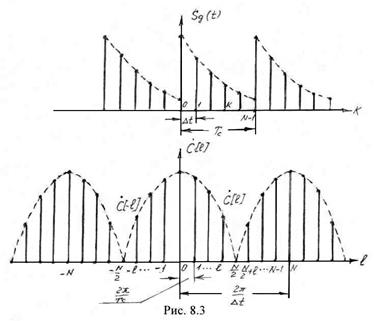 кретного сигнала, с одной стороны, является периодическим на оси частот с периодом , а спектр периодического на оси времени сигнала является линейчатым, следует ожидать, что спектр рассматриваемого ограниченного дискретного сигнала должен быть периодическим на оси частот и носить линейчатый характер. Действительно, для ограниченного во времени дискретного сигнала его представление (8.10) принимает вид

. (8.12)

Поскольку в соответствии с принятой методикой анализа является периодическим с периодом , разложим его в комплексный ряд Фурье

, (8.13)

где ; .

Комплексные амплитуды для рассматриваемого случая вычисляются следующим образом

. (8.14)

Подставляя (8.12) в (8.14), получим

.

Вводя безразмерную переменную и изменяя порядок суммирования и интегрирования, получим

.

И наконец, учитывая фильтрующее свойство -функции, окончательно приходим к результату

. (8.15)

Ввиду того, что является постоянной величиной, ее в (8.15) можно опустить и пользоваться только номерами отсчетов (8.15) принимает вид

. (8.16)

Выражение (8.16) является прямым дискретным преобразованием Фурье (ДПФ) и представляет собой алгоритм вычисления спектральных коэффициентов при известных значениях отсчетов . При этом, вычисления проводятся с использованием математических операций сложения, умножения и задержки средствами ЭВТ.

Совокупность представляет собой дискретный спектр периодического дискретного сигнала. На рис. 8.3б изображена спектральная функция дискретного сигнала. Как и предполагалось, спектральная функция является периодической с периодом , поскольку периодическим является сомножитель в (8.16) и дискретный сигнал также рассматривается как периодический (значения аргумента повторяются через каждые отсчетов). При этом, если число отсчетов дискретного сигнала четное, то первые значений составляющих соответствуют положительным частотам, а последующие значений , а также – отрицательным частотам (рис. 8.3б). Очевидно, что .

В дальнейшем удобно представлять дискретный сигнал в виде дискретной последовательности отсчетов . Тогда, в качестве периода дискретного сигнала выступает значение числа отсчетов и последовательность является периодической с периодом . Аналогично и спектральная функция является дискретной по оси частот последовательностью с тем же периодом .

Наряду с прямым ДПФ существует и обратное преобразование Фурье

. (8.17)

Обратное ДПФ позволяет рассчитать последовательность отсчетных значений , т.е. дискретный сигнал, если известна его спектральная функция в виде совокупности значений . Очевидно, обратное ДПФ приводит к периодической временной функции с периодом в отсчетов.

Отметим важное для практического использования ДПФ обстоятельство. При выводе (8.16) предполагалось, что дискретный сигнал представляет собой периодическую функцию времени. Вместе с тем на практике дискретный сигнал определен на интервале или на интервале . Вне этого интервала отсчетные значения равны нулю, однако и в этом случае выражения (8.16) и (8.17) справедливы для расчетов. Действительно, последовательность отсчетов , определенных на интервале , можно рассматривать как только один период соответствующей периодической последовательности и значения , рассчитанные в соответствии с (8.16) следует считать равными нулю вне интервала . Аналогично, обстоит дело и при вычислении значений по формуле (8.17).

Рассмотрим некоторые свойства ДПФ. Для краткости записи пару ДПФ будем представлять в виде

.

1.                Линейность ДПФ. Пусть и два дискретных сигнала длиной отсчетов, а и – постоянные коэффициенты. Тогда

. (8.18)

2.                Свойство временного сдвига. Если дискретному сигналу соответствует ДПФ , то

, (8.19)

т.е. сдвиг дискретного сигнала на интервалов приводит к изменению только его фазового спектра. Отметим, что временной сдвиг для дискретной последовательности представляет собой, так называемый круговой сдвиг. При круговом сдвиге значения отсчетов в зависимости от знака поочередно переносятся в начало или конец последовательности . Так, например, круговой сдвиг последовательности на интервалов при приводит к последовательности

,

т.е. отсчетов поочередно переносятся в конец последовательности.

3. Свойство симметрии. Это свойство фактически было уже рассмотрено выше при анализе спектральной функции (рис. 8.3б). Если – четное число, то свойство симметрии определяется следующим выражением

. (8.20)

Приведем некоторые соотношения, вытекающие из (8.16).

Спектральная составляющая

, (8.21)

является средним значением всех отсчетов.

Если – четное число, то

. (8.22)

8.3. Быстрое преобразование Фурье

Основная трудность вычисления ДПФ при длинных последовательностях заключается в большом количестве арифметических операций, что требует высокого быстродействия вычислительных средств и значительного времени обработки. Так например, для определения спектра последовательности длиной в соответствии с (8.16) требуется комплексных умножений и комплексных сложений. Это в ряде случаев делает затруднительной обработку сигнала в реальном масштабе времени. Быстрое преобразование Фурье (БПФ) позволяет сократить число арифметических операций на несколько порядков.

Основная идея БПФ заключается в разбиении последовательности на подпоследовательности, вычислении ДПФ для каждой из них и объединении результатов вычислений. Наиболее просто алгоритм БПФ реализуется в случае , где – натуральное число. Если , то последовательность дополняется нулями.

Рассмотрим процедуру БПФ на примере деления последовательности на две подпоследовательности. Будем полагать, что в первую подпоследовательность входят значения с четными, а во вторую – с нечетными номерами. Тогда выражение (8.16) принимает вид

. (8.23)

Введем следующие обозначения: подпоследовательность с четными номерами обозначим через , а с нечетными номерами – через . Тогда выражение (8.23) принимает вид

, (8.24)

– четные – нечетные

где .

Но первая сумма в (8.24) представляет собой ДПФ подпоследовательности отсчетов с четными номерами

,

а вторая сумма – ДПФ подпоследовательности отсчетов с нечетными номерами:

.

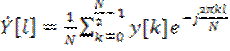Тогда вместо (8.24) получаем выражение

, при . (8.25)

При в силу периодичности спектра дискретной последовательности

, при . (8.26)

Выражения (8.25) и (8.26) представляют собой алгоритм БПФ. Вычислительная схема БПФ может быть представлена в следующем виде (рис. 8.4).

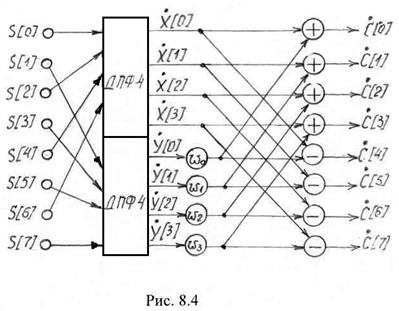
Нетрудно убедиться, что число операций для вычисления сокращается приблизительно в два раза. Если провести дальнейшее разбиение подпоследовательностей и на более короткие подпоследовательности и использовать алгоритм БПФ, аналогичный рассмотренному, то можно добиться еще большего сокращения числа операций.

8.4. Общее описание дискретной цепи. Линейное разностное уравнение

Прежде чем преступить к рассмотрению дискретных цепей, отметим, что аналоговый сигнал может быть подвергнут цифровой обработке в соответствии со структурной схемой, изображенной на рис. 8.5.

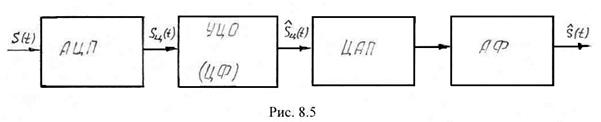
Входной аналоговый сигнал при помощи аналого-цифрового преобразователя преобразуется в цифровой сигнал . Цифровой сигнал поступает в устройство цифровой обработки (УЦО), представляющее собой вычислительное устройство. В УЦО производится обработка по заданному алгоритму, включающему арифметические операции сложения, умножения, а также операцию задержки во времени. Эти операции выполняются средствами ЭВТ, поэтому в качестве УЦО выступают специализированные ЭВМ.

Среди разнообразных алгоритмов обработки цифровых сигналов наибольшее распространение получила цифровая фильтрация, включающая в себя цифровой спектральный анализ. Поэтому в дальнейшем под УЦО будем подразумевать цифровой фильтр (ЦФ). На выходе ЦФ формируется новый сигнал , который после цифро-аналогового преобразования и прохождения через аналоговый фильтр является сигналом прошедшим цифровую обработку.

Цифровые сигналы, обрабатываемые в ЦФ дискретны во времени и квантованы по уровню. Кроме того все коэффициенты математических операций также квантованы. Учет квантованности сигналов и коэффициентов усложняет анализ цифровых систем. Поэтому для упрощения анализа полагают, что входные сигналы, подвергаемые цифровой обработке, дискретизированы по времени, но не квантованы (шаг квантования бесконечно мал) и предполагается, что коэффициенты фильтра могут принимать любые значения в заданном диапазоне. В этом случае УЦО может быть представлено в виде дискретной цепи, которая осуществляет операцию преобразования одной дискретной последовательности в другую.

Придерживаясь методике анализа и обозначений непрерывных цепей будем в общем случае представлять дискретную цепь в виде «черного ящика» (рис. 8.6), на вход которого поступает входная дискретная последовательность

,

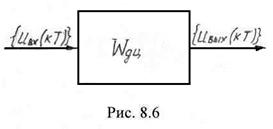где принимает значения от до , а представляет собой промежутки времени между соседними отсчетами последовательности, и на выходе формируется выходная последовательность . Дискретная последовательность (входная или

выходная) математически описывается в виде набора чисел

. (8.27)

Поскольку промежутки времени между значениями последовательности одинаковы, то этот параметр при описании дискретной последовательности часто опускают

. (8.28)

Так же, как и непрерывные, дискретные цепи могут быть линейными и нелинейными. Дискретная цепь является линейной, если

, (8.29)

где – оператор преобразования дискретной цепи.

Аналогично непрерывным цепям дискретные цепи могут быть с постоянными или переменными параметрами.

Если ,

то для цепи с постоянными параметрами

,

т.е. задержка во времени входной последовательности на тактов приведет к такой же задержке и выходной последовательности. Поскольку в практике цифровой обработки подавляющее распространение получили линейные цепи с постоянными параметрами, именно этому классу цепей будет уделено основное внимание.

Дискретные линейные цепи можно описать уравнениями, связывающими входной и выходной сигналы. В отличие от непрерывных линейных цепей, которые описываются линейными дифференциальными уравнениями, дискретные цепи описываются линейными разностными уравнениями.

В качестве примера рассмотрим дискретный аналог непрерывной – цепи первого порядка, которая описывается уравнением:

, (8.30)

где – постоянная времени цепи.

При описании дискретной цепи производная по времени заменяется конечной разностью:

.

Тогда с учетом этого, после несложных преобразований можно получить

, (8.31)

где ; .

Выражение (8.31) представляет линейное разностное уравнение первого порядка, описывающее дискретный аналог непрерывной –цепи.

В общем случае дискретная линейная цепь описывается линейным разностным уравнением -го порядка

. (8.32)

Таким образом, уравнение (8.32) определяет очередной -тый отсчет выходного сигнала с учетом предыдущих значений выходного сигнала и предыдущих значений входного сигнала и полностью описывает дискретную линейную цепь.

8.5. Основные характеристики дискретной линейной цепи

При изучении непрерывных цепей было установлено, что описание таких цепей можно проводить при помощи временных и частотных характеристик. Аналогичные характеристики можно определить для линейных дискретных цепей.

Импульсная характеристика линейной дискретной цепи представляет собой отклик (реакцию) цепи на входной сигнал в виде единичного импульса (единичного отсчета)

, (8.33)

где единичный импульс характеризуется следующими параметрами

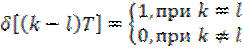. (8.34)

Так, например, импульсная характеристика цепи, описываемой уравнением

, (8.35)

определяется, если положить

. (8.36)

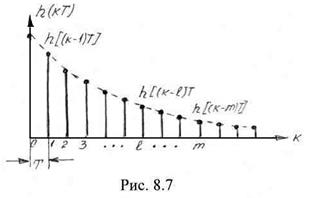
и представляет собой последовательность отсчетов, которые совпадают с коэффициентами . Действительно, в соответствии с (8.34) при , при и т.д. Иными словами для рассматриваемой цепи

. (8.37)

Тогда уравнение (8.35) с учетом (8.37) можно записать следующим образом

. (8.38)

Из условия физической реализуемости цепи

, при ,

что означает, что отклик не может появиться раньше входного сигнала верхний предел суммы (8.38) можно заменить на k и тогда

. (8.39)

Уравнение (8.39) представляет собой дискретный аналог интеграла Дюамеля. Таким образом, как и в непрерывной цепи, сигнал на выходе дискретной цепи представляет собой свертку входного сигнала и импульсной характеристики цепи. Однако, в отличие от интеграла Дюамеля свертка (8.39) называется дискретной.

Возвратимся к разностному уравнению (8.32) и представим его в виде:

.. (8.40)

Применим к обеим частям этого уравнения преобразование Лапласа с учетом того, что

.

Тогда уравнение (8.40) принимает вид

.

Передаточная функция дискретной цепи

. (8.41)

Подставляя в это выражение , получим комплексный коэффициент передачи дискретной цепи

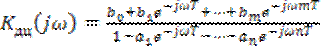. (8.42)

Очевидно, АЧХ и ФЧХ цепи определяется как модуль и аргумент выражения (8.42).

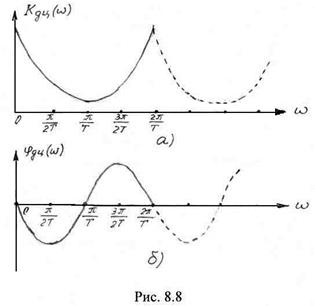
В качестве примера найдем комплексный коэффициент передачи цепи, описываемой уравнением (8.31). Приводя это уравнение к виду (8.40), после несложных преобразований получим

.

Амплитудно-частотная характеристика цепи (рис. 8.8а)

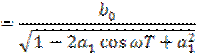
и фазо-частотная характеристика (рис. 8.8б)

,

имеют периодический характер, что свойственно для всех дискретных цепей.

8.6. Z-преобразование и системная функция дискретной цепи

В выражение (8.41) входят функции . Наличие трансцендентных функций затрудняет анализ дискретных сигналов и цепей. Для упрощения анализа удобно сделать замену

, где .

При такой замене указанные трансцендентные функции комплексной переменной преобразуются в соответствующие -изображения, являющиеся алгебраическими функциями переменной . Преобразование в плоскость осуществляется при помощи следующих соотношений, связывающих координаты какой-либо точки на плоскости с координатами соответствующей точки на плоскости :

,

; . (8.43)

Например, точка с координатами , со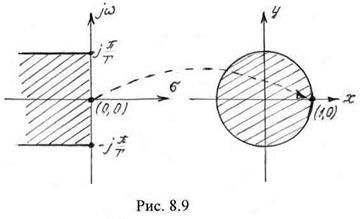 ответствует точке с координатами , (рис. 8.9). При движении точки на плоскости вдоль оси соответствующая ей точка описывает окружность единичного радиуса на -плоскости. При этом один оборот точки соответствует изменению частоты от до . Точки, лежащие в левой полуплоскости внутри области однозначно отображаются внутри круга единичного радиуса - плоскости.

Пусть дискретная последовательность представлена в виде

.

Тогда преобразование такой последовательности

,

представляет собой ряд и определено только для тех значений , при которых этот ряд сходится.

Отметим некоторые свойства - преобразования:

1. Линейность. Если последовательности соответствует - преобразование , а последовательности – z-преобразование , то

. (8.44)

2. -преобразование задержанной последовательности. Пусть последовательность является задержанной на n тактов. Ее -преобразование

. (8.45)

Таким образом, при задержке последовательности на тактов необходимо умножить ее -преобразование на .

Возвратимся к выражению (8.40). Применяя к обеим частям уравнения -преобразование с учетом второго свойства (8.45), получим:

,

откуда следует

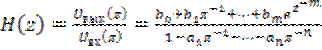. (8.46)

Отношение (8.46) называется системной функцией дискретной цепи. Системная функция для дискретной цепи играет ту же роль, что и комплексный коэффициент передачи или передаточная функция для непрерывной цепи.

Обратимся к выражению (8.39). Применяя -преобразование к обеим частям выражения, получим

,

откуда следует, что системная функция представляет собой –преобразование импульсной характеристики цепи.

8.7. Цифровые фильтры

Цифровым фильтром называется физическое устройство или программа вычислений на ЭВМ, реализующее преобразование (8.32) или, что то же самое, алгоритм цифровой фильтрации.

Физически осуществимые цифровые фильтры, которые работают в реальном масштабе времени для формирования выходного сигнала в -тый дискретный момент времени могут использовать данные двух типов

– текущий и некоторое количество предыдущих отсчетов входного сигнала;

– помимо текущего и некоторого количества предыдущих отсчетов входного сигнала еще и некоторое количество предыдущих отсчетов выходного сигнала.

Целые числа и , причем определяют порядок цифрового фильтра.

Фильтры, использующие для формирования выходного сигнала только отсчеты входного сигнала, получили название трансверсальных фильтров. Фильтры же, использующие для формирования выходного сигнала не только отсчеты входного, но предыдущие отсчеты выходного сигнала называются рекурсивными цифровыми фильтрами.

Начнем с рассмотрения трансверсальных (нерекурсивных) фильтров. Так как в таких фильтрах текущий отсчет выходного сигнала определяется только отсчетом входного сигнала, алгоритм фильтрации как это следует из (8.32) записывается следующим образом

. (8.47)

Здесь – порядок трансверсального фильтра.

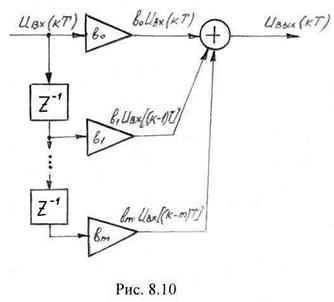
Структурная схема трансверсального фильтра изображена на рис. 8.10. Основными элементами фильтра служат элементы задержки отсчетных значений входного сигнала на один интервал дискретизации (прямоугольники ) и перемножители (прямоугольники), осуществляющие перемножение соответствующих отсчетных значений на масштабные коэффициенты , где . С выходов перемножителей сигналы поступают на сумматор, где складываясь, образуют отсчет выходного сигнала . Нетрудно убедиться, что трансверсальный фильтр представляет собой дискретную цепь без обратной связи.

Отметим, что элемент задержки га один такт обозначен через на основании (8.45), из которого следует, что при задержке последовательности на один такт ее  преобразование умножается на .

Рассмотрим характеристики трансверсального фильтра. Импульсная характеристика, как было определено выше, представляет собой отклик фильтра на входной сигнал вида (выражение (8.34)). Ранее, уже была определена импульсная характеристика дискретной цепи, описываемой уравнением (8.35), что полностью соответствует (8.47) – уравнению трансверсального фильтра. Импульсная характеристика представляет собой последовательность чисел:

.

В этом нетрудно убедится, рассматривая работу схемы, изображенной на рис. 8.10. В начальный момент времени и сигнал на выходе . В следующий момент времени с номером такта задержанный на длительность такта единичный импульс умножится на масштабный коэффициент и выходной сигнал будет равен и т.д. Отметим, что в реальных физически реализуемых фильтрах его порядок представляет собой конечное число. А это значит, что импульсная характеристика фильтра является конечной последовательностью. Поэтому, трансверсальные фильтры имеют еще одно название – фильтры с конечной импульсной характеристикой или КИХ – фильтры.

Системная функция. Применим к (8.47) -преобразование:

,

откуда

. (8.48)

Таким образом, системная функция трансверсального фильтра является дробно-рациональной функцией.

Комплексный коэффициент передачи. Производя в (8.47) замену , получим выражение для комплексного коэффициента передачи:

. (8.49)

Очевидно, из (8.49) можно получить выражения для амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристик. При заданном шаге дискретизации можно реализовать самые разнообразные формы АЧХ, подбирая должным образом коэффициенты .

Трансверсальные фильтры получили широкое распространение вследствие простоты реализации. Вместе с тем, для получения хороших частотных характеристик необходимы фильтры высокого порядка ( достигает величины несколько сотен). Это сдерживает применение трансверсальных фильтров.

Если для формирования текущего отсчета выходного сигнала используются предыдущие отсчеты как входного, так и выходного сигналов, такие фильтры, как подчеркивалось выше, называются рекурсивными.

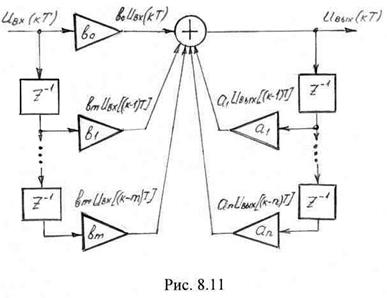В общем случае рекурсивный фильтр описывается линейным разностным уравнением (8.32), а схема устройства, реализующего алгоритм фильтрации (8.32) изображена на рис. 8.11.

Как следует из рисунка рекурсивный фильтр содержит нерекурсивную часть, идентичную рассмотренному выше трансверсальному фильтру и рекурсивную часть , состоящую из линии задержки и перемножителей на масштабные коэффициенты . Рекурсивная часть фильтра использует предшествующих значений выходного сигнала для формирования его текущего значения. Таким образом, рекурсивный фильтр является дискретной линейной цепью с обратной связью.

Рассмотрим основные характеристики рекурсивного фильтра.

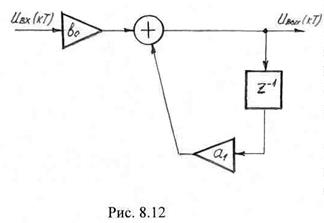
Импульсная характеристика. Так как рекурсивный фильтр представляет собой дискретную цепь с обратной связью следует ожидать, что его импульсная характеристика имеет характер бесконечной последовательности. Убедимся в этом на примере цепи, описываемой уравнением (8.31), структурная схема которой представлена на рис. 8.12.

Очевидно, рассматриваемая цепь представляет собой рекурсивный фильтр первого порядка. Пусть входной сигнал представляет собой единичный импульс, т.е. . Рассмотрим по тактам последовательность отсчетов на выходе фильтра.

При , ;

при , ;

при ,

при , и т.д.

Таким образом, импульсная характеристика фильтра:

, (8.50)

представляет собой геометрическую прогрессию, убывающую при . Подобная ситуация имеет место для любого рекурсивного фильтра. Поэтому рекурсивные фильтры получили также название фильтров с бесконечной импульсной характеристикой или БИХ - фильтров.

Системная функция. Применяя к (8.32) -преобразование можно получить выражение для системной функции рекурсивного фильтра

. (8.51)

Комплексный коэффициент передачи определяется из (8.51) заменой

, (8.52)

откуда можно получить выражения для АЧХ и ФЧХ рекурсивного фильтра.

Достоинством рекурсивных фильтров является то, что рекурсивные фильтры позволяют получить хорошие частотные характеристики при меньшем значении порядка фильтра по сравнению с трансверсальными. Поскольку порядок фильтра определяет объем памяти (длину линии задержки), то рекурсивные фильтры требуют меньшего объема памяти, а следовательно меньшего объема вычислений. В то же время, поскольку рекурсивные фильтры являются цепями с обратной связью, они менее устойчивы, чем трансверсальные фильтры.

8.8. Методы синтеза цифровых фильтров

Под синтезом цифрового фильтра понимают определение его масштабных коэффициентов и , при которых обеспечиваются требуемые его характеристики.

Все методы синтеза цифровых фильтров можно разделить на две группы:

• методы, использующие в качестве прототипов, соответствующие аналоговые фильтры;
• прямые методы, использующие непосредственный поиск масштабных коэффициентов, обеспечивающих оптимальные значения характеристик фильтров. Поскольку методы синтеза аналоговых фильтров хорошо разработаны, методы первой группы нашли наиболее широкое распространение. Кратко остановимся на этих методах.

Синтез цифрового фильтра на основе перехода от дифференциального уравнения аналогового фильтра к разностному уравнению цифрового фильтра. Этот метод был использован выше при определении структуры цифрового фильтра, аналогичного – цепи (выражение (8.31) и рис. 8.2).

Синтез цифрового фильтра на основе дискретизации импульсной характеристики аналогового фильтра прототипа. Суть метода состоит в том, что импульсная характеристика фильтра – прототипа подвергается дискретизации с интервалом , т.е. определяется . Далее с помощью -преобразование определяется системная функция

, (8.53)

которая и дает структуру фильтра.

Синтез цифрового фильтра на основе перехода передаточной функции аналогового фильтра к системной функции цифрового фильтра. Переход от к в этом случае осуществляется с помощью так называемого билинейного преобразования

, (8.54)

т.е. в заменяют в соответствии с выражением (8.54). Оценка качества каждого метода приведена в рекомендованной литературе.

Список рекомендуемой литературы

1.    С.И. Баскаков. Радиотехнические цепи и сигналы. – М.: Высшая школа, 2000

2.    И.С. Гоноровский, М.П. Демин. Радиотехнические цепи и сигналы – М.: Радио и связь, 1994

3.    Радиотехнические цепи и сигналы. Учебные пособия для ВУЗов/ под ред. К.А. Самойло – М.: Радио и связь, 1982

4.    С.И. Баскаков. Радиотехнические цепи и сигналы. Руководство по решению задач. – М.: Высшая школа, 2002

5.    Радиотехнические цепи и сигналы. Примеры и задачи/ под ред. И.С. Гоноровского. – М.: Радио и связь, 1989

6.    Радиотехнические цепи и сигналы. Задачи и задания/ под ред. А.Н. Яковлева. – М.: Инфа-М, изд-во НГТУ, 2003г.

7.    М.Т. Иванов, А.Б. Сергиенко, В.И. Ушаков. Теоретические основы радиотехники. – М.: Высшая школа, 2002г.