11.1. Широкополосная передача данных
11.2. Синтез ансамблей сигнатур для CDMA систем с прямым расширением спектра
11.3. Подходы к синтезу ансамблей сигнатур для асинхронного кодового разделения с ПРС
11.1. Широкополосная передача данных
В многопользовательской сети с кодовым разделением (CDMA) каждый из ![]() абонентов передает или принимает свои данные, используя некоторую индивидуальную сигнатуру, причем выбор ансамбля из
абонентов передает или принимает свои данные, используя некоторую индивидуальную сигнатуру, причем выбор ансамбля из ![]() сигнатур должен быть таким, чтобы гарантировать должную совместимость пользователей. Транспортировка потока данных с помощью
сигнатур должен быть таким, чтобы гарантировать должную совместимость пользователей. Транспортировка потока данных с помощью ![]() -й сигнатуры подразумевает ее модуляцию, часто – с учетом широкополосной природы CDMA сигнатур – называемую широкополосной. Различают две классические разновидности широкополосной модуляции: с прямым расширением спектра (ПРС) и с расширением спектра прыгающей частотой (ПЧРС). Первая из них гораздо характернее для современных коммерческих беспроводных приложений, поэтому обсуждение второй будет предельно кратким.
-й сигнатуры подразумевает ее модуляцию, часто – с учетом широкополосной природы CDMA сигнатур – называемую широкополосной. Различают две классические разновидности широкополосной модуляции: с прямым расширением спектра (ПРС) и с расширением спектра прыгающей частотой (ПЧРС). Первая из них гораздо характернее для современных коммерческих беспроводных приложений, поэтому обсуждение второй будет предельно кратким.
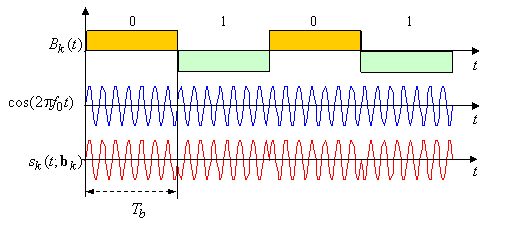
Общая идея ПРС состоит в АФМ модуляции потоком данных АФМ сигнатуры. Для облегчения усвоения идеи рассмотрим вначале простейший случай цифровой передачи данных с помощью БФМ без расширения спектра. Обозначим через ![]() информационный (модулирующий) сигнал
информационный (модулирующий) сигнал ![]() -го пользователя (см. рисунок), в котором положительные и отрицательные импульсы длительности
-го пользователя (см. рисунок), в котором положительные и отрицательные импульсы длительности ![]() передают значения информационного бита 0 и 1 соответственно. Если последовательность
передают значения информационного бита 0 и 1 соответственно. Если последовательность ![]() описывает битовый поток
описывает битовый поток ![]() -го пользователя, то
-го пользователя, то ![]() . БФМ передача сигнала данных
. БФМ передача сигнала данных ![]() означает попросту перемножение его с непрерывным гармоническим колебанием несущей частоты
означает попросту перемножение его с непрерывным гармоническим колебанием несущей частоты ![]() (см. рисунок, где четвертьпериодный сдвиг косинуса делает эпюру нагляднее), формирующее посылаемый модулированный сигнал
(см. рисунок, где четвертьпериодный сдвиг косинуса делает эпюру нагляднее), формирующее посылаемый модулированный сигнал
![]() .
.
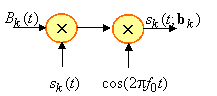
Обсудим теперь, какие изменения внесет прямое расширение в двоичную передачу данных, если ПРС реализуется с использованием БФМ последовательности. Пусть ![]() –
– ![]() -я пользовательская БФМ сигнатура, т.е. дискретный сигнал, составленный из чипов длительности
-я пользовательская БФМ сигнатура, т.е. дискретный сигнал, составленный из чипов длительности ![]() , манипулированных некоторой специфической для каждого пользователя бинарной последовательностью. Пусть на интервале одного бита данных содержится
, манипулированных некоторой специфической для каждого пользователя бинарной последовательностью. Пусть на интервале одного бита данных содержится ![]() чипов сигнатуры. Тогда ПРС БФМ сигнала данных сводится всего лишь к введению еще одного умножения на сигнатуру
чипов сигнатуры. Тогда ПРС БФМ сигнала данных сводится всего лишь к введению еще одного умножения на сигнатуру ![]() :
:
![]() .
.
Поскольку полосы упомянутых выше сигналов обратны длительностям бита ![]() и чипа
и чипа ![]() соответственно, ПРС расширяет спектр в
соответственно, ПРС расширяет спектр в ![]() раз. Последний факт оправдывает еще одно наименование частотно-временного произведения и выигрыша от обработки
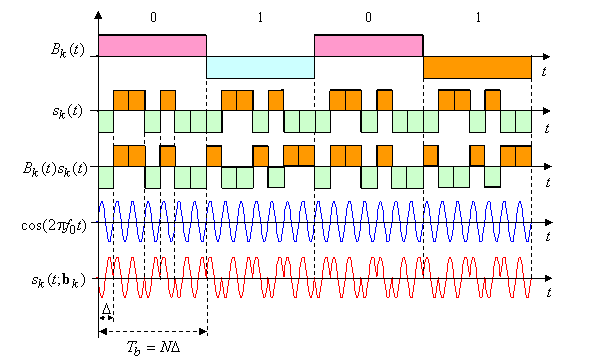
раз. Последний факт оправдывает еще одно наименование частотно-временного произведения и выигрыша от обработки ![]() – коэффициент расширения. Технически операции умножения могут быть выполнены в произвольном порядке, например, как показывают рисунок на предыдущем слайде (ПРС бинарной
– коэффициент расширения. Технически операции умножения могут быть выполнены в произвольном порядке, например, как показывают рисунок на предыдущем слайде (ПРС бинарной ![]() -последовательностью длины
-последовательностью длины ![]() ), битовый поток
), битовый поток ![]() можно вначале умножить на сигнатуру
можно вначале умножить на сигнатуру ![]() , модулируя далее непрерывную несущую произведением
, модулируя далее непрерывную несущую произведением ![]() . Можно сказать, что в этом случае битовый поток сперва модулирует бинарную видеосигнатуру, а затем результат используется для бинарной ФМ несущей.
. Можно сказать, что в этом случае битовый поток сперва модулирует бинарную видеосигнатуру, а затем результат используется для бинарной ФМ несущей.
В результате распространения по каналу сигнал приобретает задержку ![]() и начальную фазу
и начальную фазу ![]() , а также испытывает ослабление, которое далее игнорируется как не влияющее на анализируемые эффекты, имея на входе приемника вид
, а также испытывает ослабление, которое далее игнорируется как не влияющее на анализируемые эффекты, имея на входе приемника вид
![]() .
.
Типичный БФМ-приемник содержит петли временной и фазовой синхронизации, оценивающие текущие значения задержки ![]() и начальной фазы
и начальной фазы ![]() . На данном этапе вопрос о точности оценивания можно оставить в стороне, полагая, что приемнику известны истинные значения
. На данном этапе вопрос о точности оценивания можно оставить в стороне, полагая, что приемнику известны истинные значения ![]() и
и ![]() .
.
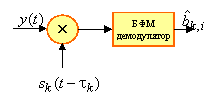
Тогда приемник для восстановления текущего (![]() -го) бита должен лишь сделать выбор между сигналом
-го) бита должен лишь сделать выбор между сигналом ![]() и его противофазной копией. Для оптимального выполнения этой операции следует вычислить корреляцию
и его противофазной копией. Для оптимального выполнения этой операции следует вычислить корреляцию
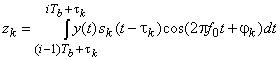
между наблюдаемым колебанием ![]() и местной опорной копией сигнатуры
и местной опорной копией сигнатуры ![]() , и вынести решение соответственно полярности
, и вынести решение соответственно полярности ![]() . Эту же оптимальную процедуру можно, однако, выполнить в два этапа, устранив сначала расширение спектра, а затем осуществив обычную демодуляцию данных, как если бы они были переданы без всякого расширения. Предположим, наблюдение
. Эту же оптимальную процедуру можно, однако, выполнить в два этапа, устранив сначала расширение спектра, а затем осуществив обычную демодуляцию данных, как если бы они были переданы без всякого расширения. Предположим, наблюдение ![]() умножается на формируемую в приемнике видеокопию
умножается на формируемую в приемнике видеокопию ![]() сигнатуры, точно синхронизированную с принимаемым сигналом. Полезная составляющая наблюдения после этой операции изменяется как
сигнатуры, точно синхронизированную с принимаемым сигналом. Полезная составляющая наблюдения после этой операции изменяется как
![]() ,
,
где учтена бинарность сигнатуры ![]() , в силу которой
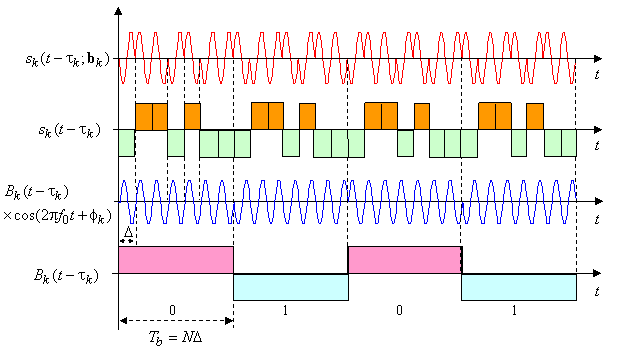
, в силу которой ![]() . Как видно, после такого шага принятый сигнал не обладает никакими чертами широкополосного, полностью повторяя сигнал несущей, бинарно манипулированной потоком данных. Вследствие этого операцию умножения наблюдения на копию сигнатуры можно назвать сжатием спектра. Следующий рисунок иллюстрирует процедуру трансформации широкополосного сигнала с прямым расширением в обычный бинарный БФМ сигнал с модуляцией потоком данных.
. Как видно, после такого шага принятый сигнал не обладает никакими чертами широкополосного, полностью повторяя сигнал несущей, бинарно манипулированной потоком данных. Вследствие этого операцию умножения наблюдения на копию сигнатуры можно назвать сжатием спектра. Следующий рисунок иллюстрирует процедуру трансформации широкополосного сигнала с прямым расширением в обычный бинарный БФМ сигнал с модуляцией потоком данных.
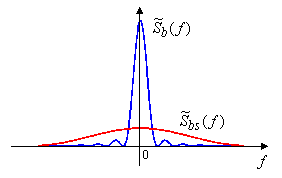
Введенные выше понятия и термины можно подкрепить кратким анализом в категориях частотной области. Для этого обратимся к следующему рисунку, на котором приведены спектральные плотности мощности ![]() исходного потока данных
исходного потока данных ![]() и его широкополосной версии
и его широкополосной версии ![]() соответственно. Для последовательности
соответственно. Для последовательности ![]() битовых импульсов длительности
битовых импульсов длительности ![]() , полярности которых случайны и независимы, спектр мощности
, полярности которых случайны и независимы, спектр мощности ![]() . Трактуя поток данных после ПРС вновь как случайную последовательность импульсов с независимыми полярностями (на этот раз длительности
. Трактуя поток данных после ПРС вновь как случайную последовательность импульсов с независимыми полярностями (на этот раз длительности ![]() ) придем к спектру мощности той же формы, но с полосой, расширенной в
) придем к спектру мощности той же формы, но с полосой, расширенной в ![]() раз:
раз: ![]() . Передача в эфире широкополосного сигнала обладает всеми преимуществами распределенного спектра, но сжатие спектра на приемной стороне возвращает его в исходную полосу, превращая сигнал в узкополосный и позволяя воспользоваться простейшими технологиями демодуляции данных.
. Передача в эфире широкополосного сигнала обладает всеми преимуществами распределенного спектра, но сжатие спектра на приемной стороне возвращает его в исходную полосу, превращая сигнал в узкополосный и позволяя воспользоваться простейшими технологиями демодуляции данных.
Идея прямого расширения спектра, рассмотренная выше применительно к БФМ передаче данных в варианте использования бинарных сигнатур, легко обобщается на более широкий диапазон сигнатур и методов модуляции данными. Пусть ![]() обозначает комплексное колебание, отвечающее потоку данных
обозначает комплексное колебание, отвечающее потоку данных ![]()
![]() -го пользователя, передаваемых в некотором цифровом формате (АМ, М-ичная ФМ, КАМ и др.). При М-ичной цифровой передаче данных
-го пользователя, передаваемых в некотором цифровом формате (АМ, М-ичная ФМ, КАМ и др.). При М-ичной цифровой передаче данных ![]() состоит из соприкасающихся прямоугольников длительности
состоит из соприкасающихся прямоугольников длительности ![]() , манипулированных комплексными символами, принадлежащими конкретному алфавиту М-ичной модуляции. Пусть
, манипулированных комплексными символами, принадлежащими конкретному алфавиту М-ичной модуляции. Пусть ![]() – комплексная огибающая CDMA сигнатуры
– комплексная огибающая CDMA сигнатуры ![]() -го пользователя. Ее алфавит может быть выбран независимо от алфавита модуляции данных, например, может быть бинарным, квадратурным, АФМ и т.д. Тогда прямое расширение означает умножение модулирующего сигнала данных
-го пользователя. Ее алфавит может быть выбран независимо от алфавита модуляции данных, например, может быть бинарным, квадратурным, АФМ и т.д. Тогда прямое расширение означает умножение модулирующего сигнала данных ![]() на сигнатуру
на сигнатуру ![]() и использование произведения
и использование произведения ![]() в качестве комплексной огибающей передаваемого сигнала:
в качестве комплексной огибающей передаваемого сигнала:
![]() .
.
Принятый полезный сигнал представляет собой задержанную и сдвинутую по фазе его копию
![]()
с комплексной огибающей
![]() .
.
Постоянство ![]() на интервале
на интервале ![]() означает, что для выделения
означает, что для выделения ![]() -го символа приемник должен произвести выбор между M конкурирующими копиями одной и той же сигнатуры
-го символа приемник должен произвести выбор между M конкурирующими копиями одной и той же сигнатуры ![]() , умноженной на различные символы данных
, умноженной на различные символы данных ![]() . При этом корреляция вида
. При этом корреляция вида
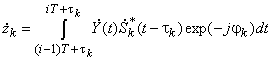
служит (после соответствующей нормировки) достаточной статистикой для вынесения нужной оценки ![]() и может трактоваться, как пара отсчетов с выходов интеграторов демодулятора, если опорным сигналом в комплексном умножителе служит
и может трактоваться, как пара отсчетов с выходов интеграторов демодулятора, если опорным сигналом в комплексном умножителе служит ![]() . После умножения на подобную опору полезная компонента наблюдаемой комплексной огибающей
. После умножения на подобную опору полезная компонента наблюдаемой комплексной огибающей
![]()
на интервале ![]() -го символа данных становится просто одной из M возможных копий видеосигнала
-го символа данных становится просто одной из M возможных копий видеосигнала ![]() , умноженного на различные комплексные коэффициенты
, умноженного на различные комплексные коэффициенты ![]() . Если чипы сигнатуры не имеют амплитудной модуляции, т.е.
. Если чипы сигнатуры не имеют амплитудной модуляции, т.е. ![]() есть ФМ сигнал,
есть ФМ сигнал, ![]() и, как видно из предыдущего равенства, умножение на
и, как видно из предыдущего равенства, умножение на ![]() переводит комплексную огибающую полезного широкополосного сигнала в форму, характерную для обычной (не широкополосной) M-ичной модуляции данными, т.е. осуществляет сжатие спектра. Благодаря этому можно вновь разбить действия приемника на два этапа: сжатие спектра, а затем обычная М-ичная демодуляция.
переводит комплексную огибающую полезного широкополосного сигнала в форму, характерную для обычной (не широкополосной) M-ичной модуляции данными, т.е. осуществляет сжатие спектра. Благодаря этому можно вновь разбить действия приемника на два этапа: сжатие спектра, а затем обычная М-ичная демодуляция.
Остановимся более подробно на техническом воплощении комплексного умножения и извлечения комплексной огибающей ![]() из реально наблюдаемого действительного колебания
из реально наблюдаемого действительного колебания ![]() . Вспомнив основные правила комплексной арифметики
. Вспомнив основные правила комплексной арифметики
![]()
![]() ,
,
можно видеть, что умножитель двух комплексных величин ![]() и
и ![]() содержит четыре обычных умножителя и два сумматора (см. рисунок). Входные комплексные операнды
содержит четыре обычных умножителя и два сумматора (см. рисунок). Входные комплексные операнды ![]() задаются своими реальными и мнимыми частями, а выходом служит пара из вещественной и мнимой частей произведения
задаются своими реальными и мнимыми частями, а выходом служит пара из вещественной и мнимой частей произведения ![]() .
.
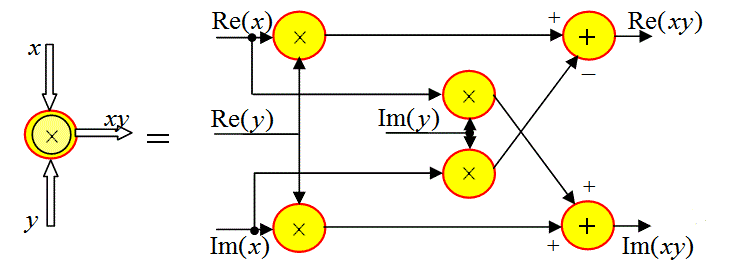
Получение комплексной огибающей наблюдения основывается на определении ![]() :
: ![]() . Применяя правило комплексного умножения и формулу Эйлера, имеем
. Применяя правило комплексного умножения и формулу Эйлера, имеем ![]() . Умножение обеих частей этого выражения на
. Умножение обеих частей этого выражения на ![]() и
и ![]() , после применения тригонометрических тождеств приводит к равенствам:
, после применения тригонометрических тождеств приводит к равенствам:
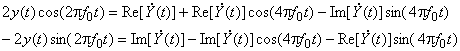 .
.
Первые слагаемые правых частей этих равенств – колебания видеочастоты (поскольку комплексная огибающая есть закон модуляции, т.е. низкочастотна по определению), тогда как остальные являются радиосигналами с центральной частотой ![]() . Ширина спектра закона модуляции значительно меньше
. Ширина спектра закона модуляции значительно меньше ![]() . Следовательно, фильтр нижних частот (ФНЧ) легко отфильтрует высокочастотные компоненты, пропустив на выход только вещественную и мнимую части желаемой комплексной огибающей
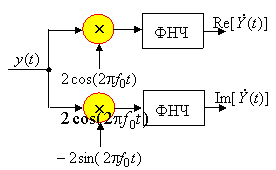
. Следовательно, фильтр нижних частот (ФНЧ) легко отфильтрует высокочастотные компоненты, пропустив на выход только вещественную и мнимую части желаемой комплексной огибающей ![]() . Описанная техника восстановления комплексной огибающей из действительного наблюдения
. Описанная техника восстановления комплексной огибающей из действительного наблюдения ![]() реализуется схемой на рисунке.
реализуется схемой на рисунке.
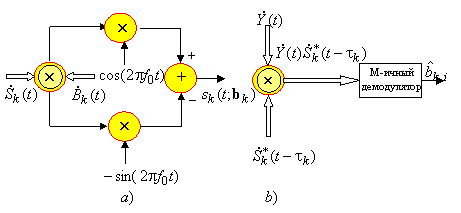
Как итог предыдущего обсуждения рисунок справа иллюстрирует базовые операции, выполняемые передающей и приемной сторонами в общей схеме широкополосной системы с прямым расширением спектра. Модулятор (рисунок а) реализует алгоритм расширения спектра, удерживая только вещественную часть комплексного произведения. В демодуляторе (рисунок b) комплексная огибающая наблюдения, восстановленная согласно ранее приведенной схемы, вначале подвергается сжатию спектра перемножением с опорой ![]() , после чего подается на вход стандартного М-ичного демодулятора для выработки решения о принятых символах.
, после чего подается на вход стандартного М-ичного демодулятора для выработки решения о принятых символах.
При расширении спектра за счет прыгающей частоты используются ЧМ сигнатуры, и модуляция данными также, как правило, выполняется с помощью ЧМ. В зависимости от соотношения между длительностями чипа ![]() и символа данных
и символа данных ![]() ПЧРС традиционно классифицируют на две разновидности: быстрое и медленное. Для быстрого ПЧРС
ПЧРС традиционно классифицируют на две разновидности: быстрое и медленное. Для быстрого ПЧРС ![]() , где
, где ![]() – натуральное число, тогда как для медленного –
– натуральное число, тогда как для медленного –![]() , где
, где ![]() – натуральное. Другими словами, при быстром ПЧРС на один символ данных приходится несколько скачков частоты, тогда как при медленном – в течение одного символа сигнатуры может быть передано несколько символов данных. Чтобы лучше понять существо ПЧРС, обратимся к примерам.
– натуральное. Другими словами, при быстром ПЧРС на один символ данных приходится несколько скачков частоты, тогда как при медленном – в течение одного символа сигнатуры может быть передано несколько символов данных. Чтобы лучше понять существо ПЧРС, обратимся к примерам.
Пример 11.1.1. Позаимствуем ЧМ сигнатуру из примера 10.1.1 для расширения спектра быстрым ПЧРС в комбинации с бинарной ЧМ данными. При этом число различных частот сигнатуры ![]() , ее длина
, ее длина ![]() , и один символ данных передает один бит информации, так что
, и один символ данных передает один бит информации, так что ![]() . Предположим, что в схеме быстрого ПЧРС
. Предположим, что в схеме быстрого ПЧРС ![]() , т.е. на один бит данных приходится 8 скачков частоты. Тогда вся последовательность ЧМ чипов передается в течение одного бита.
, т.е. на один бит данных приходится 8 скачков частоты. Тогда вся последовательность ЧМ чипов передается в течение одного бита.
Если бит данных равен нулю, этот частотный профиль передается на несущей частоте ![]() , тогда как для бита, равного единице, несущая частота принимает значение
, тогда как для бита, равного единице, несущая частота принимает значение ![]() . Естественно, разность между частотами
. Естественно, разность между частотами ![]() и
и ![]() должна быть не меньше полосы, занимаемой сигнатурой, т.е.
должна быть не меньше полосы, занимаемой сигнатурой, т.е. ![]() . На рисунке (a) следующего слайда изображен передаваемый частотный профиль, соответствующий потоку битов данных вида
. На рисунке (a) следующего слайда изображен передаваемый частотный профиль, соответствующий потоку битов данных вида ![]() . Как можно видеть, спектр одиночного бита данных, полоса которого до расширения была примерно
. Как можно видеть, спектр одиночного бита данных, полоса которого до расширения была примерно ![]() , расширяется до полосы
, расширяется до полосы ![]() , т.е. становится в
, т.е. становится в ![]() раз шире.
раз шире.
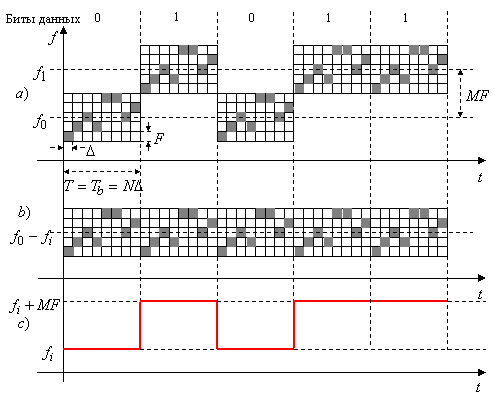
На приемной стороне сжатие спектра выполняется обычно переносом наблюдаемого колебания вниз на промежуточную частоту ![]() . С этой целью используется гетеродинирование опорной несущей
. С этой целью используется гетеродинирование опорной несущей ![]() , модулированной в соответствии с профилем ЧМ сигнатуры с необходимой задержкой во времени (рисунок (b)). Как результат, сигнал промежуточной частоты оказывается обычным узкополосным колебанием, частотно-манипулированным передаваемыми данными, где нулевой бит соответствует низкой частоте, а единичный – высокой. Таким образом, спектр отдельного символа данных сжимается до прежней ширины
, модулированной в соответствии с профилем ЧМ сигнатуры с необходимой задержкой во времени (рисунок (b)). Как результат, сигнал промежуточной частоты оказывается обычным узкополосным колебанием, частотно-манипулированным передаваемыми данными, где нулевой бит соответствует низкой частоте, а единичный – высокой. Таким образом, спектр отдельного символа данных сжимается до прежней ширины ![]() , позволяя использовать стандартный бинарный ЧМ демодулятор для восстановления принятых данных.
, позволяя использовать стандартный бинарный ЧМ демодулятор для восстановления принятых данных.
Следующий пример поясняет идею медленного ПЧРС.
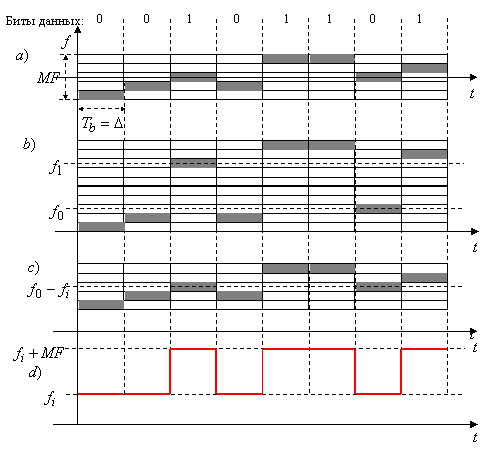
Пример 11.1.2. Используем прежнюю сигнатуру вновь в комбинации с бинарной ЧМ данными, положив равными длительности чипа и символа данных: ![]() . Последнее означает, что текущая частота остается постоянной в течение всей длительности бита данных, и скачки частоты происходят только при переходе от бита к биту. Частотный профиль сигнатуры
. Последнее означает, что текущая частота остается постоянной в течение всей длительности бита данных, и скачки частоты происходят только при переходе от бита к биту. Частотный профиль сигнатуры ![]() -кратно растягивается во времени и его длина охватывает
-кратно растягивается во времени и его длина охватывает ![]() битов данных (см. рисунок (а)). Предположим, что в течение бита данных с номером
битов данных (см. рисунок (а)). Предположим, что в течение бита данных с номером ![]() частота сигнатуры равна
частота сигнатуры равна ![]() . Тогда передаваемая частота становится равной
. Тогда передаваемая частота становится равной ![]() в случае нулевого бита данных и
в случае нулевого бита данных и ![]() для бита, равного единице. Рисунок (b) показывает последовательность передаваемых частот для битового потока
для бита, равного единице. Рисунок (b) показывает последовательность передаваемых частот для битового потока ![]() . Принципиальное различие быстрого и медленного ПЧРС очевидно: медленное не расширяет спектр отдельного символа данных, увеличивая только общую полосу, занимаемую системой. Система попросту время от времени переходит с одной рабочей частоты на другую, причем внутри группы символов данных фиксированной длины переключений не происходит. На приемной стороне перенос спектра на промежуточную частоту
. Принципиальное различие быстрого и медленного ПЧРС очевидно: медленное не расширяет спектр отдельного символа данных, увеличивая только общую полосу, занимаемую системой. Система попросту время от времени переходит с одной рабочей частоты на другую, причем внутри группы символов данных фиксированной длины переключений не происходит. На приемной стороне перенос спектра на промежуточную частоту ![]() выполняется гетеродинированием с опорной несущей
выполняется гетеродинированием с опорной несущей ![]() , модулированной ЧМ профилем (с соответствующей задержкой) сигнатуры (рисунок (с)). Эта операция возвращает колебание в полосу, соответствующую простой (без ПЧРС) ЧМ данными (рисунок (d)), после чего для восстановления передаваемых данных можно использовать стандартный ЧМ демодулятор.
, модулированной ЧМ профилем (с соответствующей задержкой) сигнатуры (рисунок (с)). Эта операция возвращает колебание в полосу, соответствующую простой (без ПЧРС) ЧМ данными (рисунок (d)), после чего для восстановления передаваемых данных можно использовать стандартный ЧМ демодулятор.
11.2. Синтез ансамблей сигнатур для CDMA систем с прямым расширением спектра
Снова напомним, что в многопользовательской сети с кодовым разделением (CDMA) каждый из ![]() абонентов передает или принимает свои данные с использованием индивидуального сигнала расширения спектра, называемого абонентской сигнатурой. Для облегчения усвоения рассмотрим случай цифровой передачи данных с помощью БФМ при ПРС с использованием БФМ последовательности. При принятии за базовый однопользовательского приемника оптимальная когерентная демодуляция бинарного ФМ сигнала с прямоугольной формой битового сигнала состоит в интегрировании на интервале длительности бита принятого колебания, умноженного на когерентный по несущей частоте образец, и принятии решения о значении бита в соответствие с полярностью напряжения после интегрирования. Поскольку приемник k-го пользовательского сигнала восстанавливает битовый поток посредством операции сжатия спектра, т.е. умножением на задержанную соответствующим образом сигнатуру k-го абонента, полезный эффект после интегрирования имеет вид
абонентов передает или принимает свои данные с использованием индивидуального сигнала расширения спектра, называемого абонентской сигнатурой. Для облегчения усвоения рассмотрим случай цифровой передачи данных с помощью БФМ при ПРС с использованием БФМ последовательности. При принятии за базовый однопользовательского приемника оптимальная когерентная демодуляция бинарного ФМ сигнала с прямоугольной формой битового сигнала состоит в интегрировании на интервале длительности бита принятого колебания, умноженного на когерентный по несущей частоте образец, и принятии решения о значении бита в соответствие с полярностью напряжения после интегрирования. Поскольку приемник k-го пользовательского сигнала восстанавливает битовый поток посредством операции сжатия спектра, т.е. умножением на задержанную соответствующим образом сигнатуру k-го абонента, полезный эффект после интегрирования имеет вид
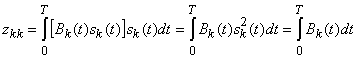
Поскольку на входе демодулятора присутствуют еще и сигналы других пользователей, то на его выходе также будет присутствовать помеха множественного доступа (ПМД). Компонент указанной помехи, обусловленный сигналом ![]() –го пользователя, представим как
–го пользователя, представим как
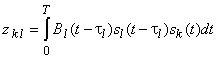
где задержка ![]()
![]() –го пользовательского сигнала определена относительно сигнала k–го пользователя, а множитель, который отвечает за ослабление, обусловленное фазовым сдвигом
–го пользовательского сигнала определена относительно сигнала k–го пользователя, а множитель, который отвечает за ослабление, обусловленное фазовым сдвигом ![]() –го сигнала, отбрасывается с целью получения оценки максимального уровня ПМД.
–го сигнала, отбрасывается с целью получения оценки максимального уровня ПМД.
Возможны два варианта построения CDMA системы.
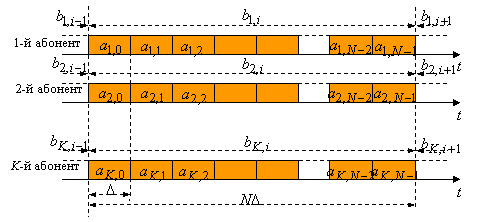
1. СинхроннаяCDMA система, в которой все абонентские потоки данных и все сигнатуры жестко синхронизованы, т.е. имеют нулевые взаимные временные сдвиги на входе приемника ![]() . Следующий рисунок подчеркивает строгое временное совпадение между чипами всех сигнатур, а также границами передаваемых символов данных в синхронном варианте CDMA. Тогда, учитывая, что сигнал
. Следующий рисунок подчеркивает строгое временное совпадение между чипами всех сигнатур, а также границами передаваемых символов данных в синхронном варианте CDMA. Тогда, учитывая, что сигнал ![]() постоянен и равен
постоянен и равен ![]() в течение длительности бита, имеем
в течение длительности бита, имеем
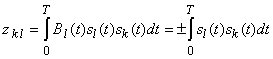 .
.
Очевидно, что оптимальным вариантом ансамбля сигнатур является такой, который гарантирует полное отсутствие помехи множественного доступа:
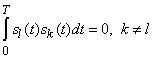
что означает ортогональность всех сигнатур. Существует множество способов построения ортогональных широкополосных ансамблей различной длины (коэффициента расширения) ![]() . Одним из примеров являются функции Уолша или, в общем случае, матрицы Адамара, порождающие ортогональные бинарные коды. Альтернативным выбором являются циклически сдвинутые копии любой последовательности с идеальной периодической АКФ, например, троичной, многофазной и др. При любом конкретном выборе ортогональных сигнатур размерность сигнального пространства
. Одним из примеров являются функции Уолша или, в общем случае, матрицы Адамара, порождающие ортогональные бинарные коды. Альтернативным выбором являются циклически сдвинутые копии любой последовательности с идеальной периодической АКФ, например, троичной, многофазной и др. При любом конкретном выборе ортогональных сигнатур размерность сигнального пространства ![]() жестко лимитирует их число (а, значит, и число пользователей
жестко лимитирует их число (а, значит, и число пользователей ![]() ):
): ![]() .
.
Если же число пользователей (сигнатур) превосходит размерность пространства ![]() , то имеет место специфический случай, называемый перенасыщением, чем подчеркивается избыточность количества сигнатурных векторов, исключающая шанс их ортогональности. Очевидно, что при этом все сигнатуры не могут быть ортогональными и, значит, присутствие ПМД неизбежно. Хорошим инструментом оценки минимально возможного уровня ПМД служит граница Велча, согласно которой полный квадрат корреляции (total squared correlation – (TSC)) во множестве из K N – мерных векторов (т.е. кодовых последовательностей сигнатур)
, то имеет место специфический случай, называемый перенасыщением, чем подчеркивается избыточность количества сигнатурных векторов, исключающая шанс их ортогональности. Очевидно, что при этом все сигнатуры не могут быть ортогональными и, значит, присутствие ПМД неизбежно. Хорошим инструментом оценки минимально возможного уровня ПМД служит граница Велча, согласно которой полный квадрат корреляции (total squared correlation – (TSC)) во множестве из K N – мерных векторов (т.е. кодовых последовательностей сигнатур) ![]() , удовлетворяет неравенству
, удовлетворяет неравенству
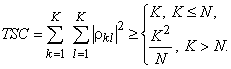
Поскольку ![]() содержит
содержит ![]() равных единице квадратов корреляций векторов с самими собой, разность
равных единице квадратов корреляций векторов с самими собой, разность ![]() включает лишь «вредные» корреляции между несовпадающими векторами, значения которых требуется иметь как можно меньшими. Всего
включает лишь «вредные» корреляции между несовпадающими векторами, значения которых требуется иметь как можно меньшими. Всего ![]() охватывает
охватывает ![]() подобных пар векторов, так что средний квадрат корреляции на одну пару сигнатур
подобных пар векторов, так что средний квадрат корреляции на одну пару сигнатур
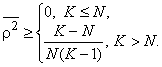
Очевидно, что ансамбль последовательностей, достигающий данной границы (последовательностей, лежащих на границе Велча), является наилучшим возможным для однопользовательского приемника по критерию минимума полной мощности ПМД и обеспечивает предельное (в пренебрежении шумом) отношение сигнал-помеха для перенасыщенного ансамбля
![]()
2. АсинхроннаяCDMA система, в которой взаимные задержки и фазовые сдвиги между отдельными пользовательскими сигналами случайны. При принятии за базовый однопользовательского приемника решение о значении текущего символа ![]() -го абонента принимается на основе корреляции
-го абонента принимается на основе корреляции
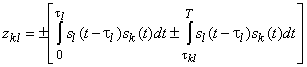 ,
,
где ![]() – задержка
– задержка ![]() -го сигнала относительно
-го сигнала относительно ![]() -го сигнала. Теперь строгое совмещение границ символов данных и чипов различных пользователей поддерживаться не может из-за произвольности относительных временных сдвигов абонентских сигналов.
-го сигнала. Теперь строгое совмещение границ символов данных и чипов различных пользователей поддерживаться не может из-за произвольности относительных временных сдвигов абонентских сигналов.

В предположении, что границы чипов всех ![]() сигналов синхронизированы, т.е. взаимные задержки кратны
сигналов синхронизированы, т.е. взаимные задержки кратны ![]() :
: ![]() , где
, где ![]() – целое, такое что
– целое, такое что ![]() , ситуация поясняется следующим рисунком (для случая k=1), подчеркивающим, что в асинхронном варианте CDMA – в отличие от синхронного – символы данных сторонних пользователей могут изменяться во время приема текущего символа
, ситуация поясняется следующим рисунком (для случая k=1), подчеркивающим, что в асинхронном варианте CDMA – в отличие от синхронного – символы данных сторонних пользователей могут изменяться во время приема текущего символа ![]() -го пользователя. В то же время главным фактором, осложняющим синтез асинхронного ансамбля, оказывается необходимость различения каждой сигнатуры со всеми возможными сдвинутыми копиями других сигнатур, отсутствующая при синхронном кодовом разделении.
-го пользователя. В то же время главным фактором, осложняющим синтез асинхронного ансамбля, оказывается необходимость различения каждой сигнатуры со всеми возможными сдвинутыми копиями других сигнатур, отсутствующая при синхронном кодовом разделении.
При выборе семейства сигнатур для асинхронных CDMA сетей типичны два подхода: детерминированный и статистический. В рамках первого подхода основной целью является гарантированное удержание максимума ПМД в пределах заранее установленного уровня, тогда как второй ориентирован на достижение приемлемого уровня ПМД в среднем.
11.3. Подходы к синтезу ансамблей сигнатур для асинхронного кодового разделения с ПРС
Детерминированный подход, как правило, базируется на предположении, что во время приема символа данных ![]() -го пользователя символы данных всех других пользователей неизменны, т.е.
-го пользователя символы данных всех других пользователей неизменны, т.е. ![]() . Тогда ситуация отличается от исследованной ранее синхронной только взаимным временным рассогласованием сигнатур. Если период сигнатуры
. Тогда ситуация отличается от исследованной ранее синхронной только взаимным временным рассогласованием сигнатур. Если период сигнатуры ![]() совпадает с выигрышем от обработки
совпадает с выигрышем от обработки ![]() , равным числу чипов на длительности одного символа данных, или, что эквивалентно, числу чипов, интегрируемых коррелятором, то уровень ПМД определяется как
, равным числу чипов на длительности одного символа данных, или, что эквивалентно, числу чипов, интегрируемых коррелятором, то уровень ПМД определяется как
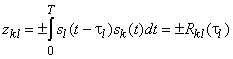 ,
,
т.е. повторяет (прямо или с противоположным знаком) значение периодической ВКФ ![]() –й и
–й и ![]() –й сигнатур. Отсюда следует первое необходимое требование, предъявляемое к сигнатурам – низкая величина их взаимной корреляции. Поскольку корреляционные функции дискретных сигналов непосредственно определяются корреляционными функциями их кодовых последовательностей (кодов), то приходим к требованию низкого уровня ВКФ
–й сигнатур. Отсюда следует первое необходимое требование, предъявляемое к сигнатурам – низкая величина их взаимной корреляции. Поскольку корреляционные функции дискретных сигналов непосредственно определяются корреляционными функциями их кодовых последовательностей (кодов), то приходим к требованию низкого уровня ВКФ ![]() –го и
–го и ![]() –го кодов сигнатур
–го кодов сигнатур ![]() и
и ![]() :
:
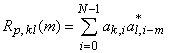 ,
,
где осуществлено обобщение на произвольный (а не только бинарный) алфавит сигнатур.
Если на диапазон возможных взаимных задержек не наложено никаких ограничений, ![]() -я сигнатура может присутствовать в виде любой из своих
-я сигнатура может присутствовать в виде любой из своих ![]() циклически сдвинутых копий, так что имеется
циклически сдвинутых копий, так что имеется ![]() различных
различных ![]() -мерных векторов, каждый из которых является потенциальным источником ПМД в
-мерных векторов, каждый из которых является потенциальным источником ПМД в ![]() -м приемнике. Следовательно, приходим к необходимости иметь в ансамбле сигнатур максимум взаимного корреляционного пика
-м приемнике. Следовательно, приходим к необходимости иметь в ансамбле сигнатур максимум взаимного корреляционного пика
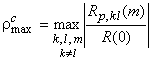
минимально возможным (основные лепестки всех АКФ полагаются одинаковыми: ![]() ).
).
Если канал подвержен эффектам многолучевости, то любая собственная циклически сдвинутая копия ![]() -го сигнала может также стать помехой
-го сигнала может также стать помехой ![]() -му приемнику. Предположим, что может существовать до
-му приемнику. Предположим, что может существовать до ![]() подобных копий, т.е. рассеяние по задержке в многолучевом канале возможно вплоть до периода сигнатуры. Другим основанием для включения собственных циклических копий в исследуемое множество векторов служит желание иметь низкий уровень автокорреляционных боковых лепестков, что важно при поиске сигнала. После подобного расширения имеется
подобных копий, т.е. рассеяние по задержке в многолучевом канале возможно вплоть до периода сигнатуры. Другим основанием для включения собственных циклических копий в исследуемое множество векторов служит желание иметь низкий уровень автокорреляционных боковых лепестков, что важно при поиске сигнала. После подобного расширения имеется ![]() векторов, корреляцию которых желательно снизить до минимума, так что и максимальный (по всем ненулевым временным сдвигам сигнатур) автокорреляционный пик
векторов, корреляцию которых желательно снизить до минимума, так что и максимальный (по всем ненулевым временным сдвигам сигнатур) автокорреляционный пик
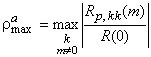
должен контролироваться по уровню.
В итоге приходим к минимаксному критерию синтеза ансамбля сигнатур, ориентированному на минимизацию корреляционного пика:
![]() .
.
В идеале в качестве сигнатур в асинхронном варианте CDMA с прямым расширением должен использоваться такой ансамбль последовательностей, все представители которого имеют идеальную периодическую АКФ и нулевую периодическую ВКФ. Последние требования явно противоречат друг другу, делая ансамбли этого сорта гипотетическими. Действительно, условия идеальности АКФ и нулевой ВКФ означают не что иное, как нулевой уровень корреляции между всеми циклическими сдвигами ![]() последовательностей периода
последовательностей периода ![]() , т.е. существование
, т.е. существование ![]() ортогональных векторов в
ортогональных векторов в ![]() –мерном пространстве, что невозможно.
–мерном пространстве, что невозможно.
Поскольку максимальное значение любой величины никогда не меньше среднего: ![]() , то для оценки корреляционного пика можно воспользоваться границей Велча с заменой
, то для оценки корреляционного пика можно воспользоваться границей Велча с заменой ![]() на
на ![]()
![]() ,
,
устанавливающей нижнюю границу минимально возможного значения корреляционного пика во множестве K асинхронных сигнатур длины N.
При дополнительных ограничениях на ФМ алфавит данная граница может оказаться достаточно слабой, особенно при числе последовательностей, соизмеримом с ![]() . В частности, для достаточно больших ансамблей бинарных
. В частности, для достаточно больших ансамблей бинарных ![]() последовательностей точнее оказывается граница Сидельникова
последовательностей точнее оказывается граница Сидельникова
![]() .
.
Комбинация асимптотических (K>>1) версий указанной границы и границы Велча приводят к следующему результату

Ансамбли, для которых ![]() , достигает предела, предсказываемого границей, разумеется, оптимальны по критерию минимума корреляционного пика, и иногда называются минимаксными.
, достигает предела, предсказываемого границей, разумеется, оптимальны по критерию минимума корреляционного пика, и иногда называются минимаксными.
Альтернативой детерминированному подходу служит статистический, который ориентирует синтез сигнатур в направлении максимального сходства между помехой множественного доступа и некоторого эквивалентного случайного аддитивного шума. Напомним, что преимущество асинхронной версии CDMA в абонентской емкости основывается именно на этом подобии, что позволяет ей функционировать при отношении сигнал-(помеха + шум), которое для АФМ сигналов может быть записано в виде
![]() .
.
Не составляет труда заметить, что результаты синтеза детерминированных сигнатур в значительной степени удовлетворяют последнему соотношению. Действительно, максимальный уровень ПМД мощности, привносимый одиночным источником помехи (сторонним пользователем), относительно мощности полезного сигнала составляет
![]() ,
,
при условии, что ансамбль сигнатур оптимален относительно границы Велча. Тогда ![]() независимых источников помех создадут общий относительный уровень помех, равный
независимых источников помех создадут общий относительный уровень помех, равный
![]() ,
,
что близко выражению, которое получается обращением приведенного ранее отношения сигнал-(помеха + шум). Отличие в коэффициенте «2» объясняется «неполной» асинхронностью, допущенной автоматически сведением проблемы к рассмотрению только кодовых последовательностей, тогда как границы чипов и фазы всех сигнатур считаются синхронизированными. Близость результатов показывает, что статистический подход к синтезу сигнатур вполне адекватен и его широкое практическое использование полностью оправдано, особенно в тех случаях, когда период сигнатуры охватывает большое число передаваемых символов данных.
В идеале случайные бинарные коды сигнатур могут быть получены как результат подбрасывания правильной монеты с присвоением текущему символу кода значений +1 и –1 в зависимости от выпадения «орла» или «решетки». Все сигнатуры формируются независимо друг от друга случайным независимым выбором элементов каждой из них, т.е. подбрасыванием монеты. При подобной схеме формирования коды сигнатур представляют собой ![]() независимых дискретных по времени случайных процессов с независимыми значениями.
независимых дискретных по времени случайных процессов с независимыми значениями.
Фактически сигнатуры не могут быть строго случайными, поскольку приемник должен априори знать закон модуляции сигнатуры с тем, чтобы сформировать необходимую опору в корреляторе. Для реализации свойства случайности на базе детерминированных правил кодирования, необходимы так называемые псевдослучайные последовательности. Так, например, в стандарте IS-95 мобильного телефона базовые станции используют различные сдвиги во времени одной и той же расширенной ![]() – последовательности длины
– последовательности длины ![]() (расширение означает добавление одного избыточного символа) для различения сигналов, излучаемых разными базовыми станциями. В рассматриваемом стандарте эта «родительская» последовательность называется коротким кодом в отличие от длинного кода, реализующего асинхронный вариант CDMA в канале «вверх», в качестве которого выступает расширенная
(расширение означает добавление одного избыточного символа) для различения сигналов, излучаемых разными базовыми станциями. В рассматриваемом стандарте эта «родительская» последовательность называется коротким кодом в отличие от длинного кода, реализующего асинхронный вариант CDMA в канале «вверх», в качестве которого выступает расширенная ![]() – последовательность длины
– последовательность длины ![]() (период которой в реальном времени составляет 41 сутки). Каждому мобильному абоненту присваивается строго индивидуальный временной сдвиг этого кода.
(период которой в реальном времени составляет 41 сутки). Каждому мобильному абоненту присваивается строго индивидуальный временной сдвиг этого кода.
В стандартах третьего поколения с CDMA также находят применение псевдослучайные сигнатуры. Например, в стандарте UMTS (3GPP) для аналогичных целей используются усеченные коды Голда длины ![]() как в прямом, так и в обратном каналах.
как в прямом, так и в обратном каналах.

