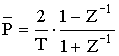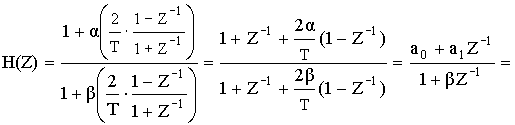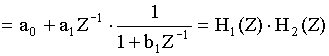При расчете рекурсивных фильтров применяются прямые и косвенные методы.

Косвенные методы предполагают в качестве промежуточного этапа расчет аналогового фильтра (АФ). Затем по передаточной функции АФ получают схему цифрового фильтра (ЦФ).

Метод билинейного преобразования.

Основой этого метода является такое преобразование частоты, при котором частотная характеристика АФ сжимается до конечных размеров. В результате ошибок наложения, которые всегда существуют при переходе от АФ к ЦФ, частотные преобразования осуществляются с помощью выражения:

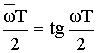где

ω – реальная частота (частота ЦФ). Тогда: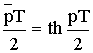

Соотношение между реальной и расчетной частотой удобно изобразить на графике.

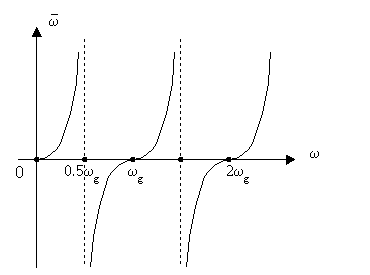
Рассмотрим графически, как преобразуется частотная характеристика АФ в частотную характеристику ЦФ.

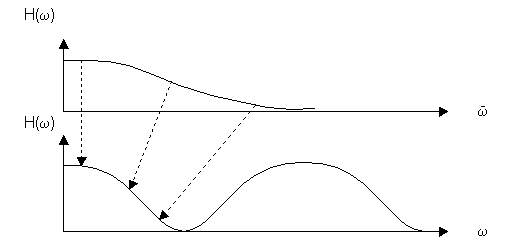
Рассмотрим соотношение частот pи по отношению к Z-плоскости.

Соотношение между P и Z:

Соотношение между и Z-плоскостью:

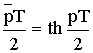, тогда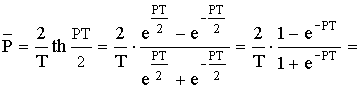

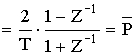
Последовательность расчета по методу билинейного преобразования.

1) Задано: норма на АФ переходит на ЦФ.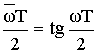

2) Рассчитать АФ в соответствии с полученными нормами. В результате расчетов становится известной передаточная характеристика H().

3) Определить H(Z) по H() применяя формулу: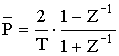

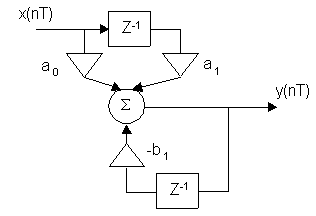
4) По передаточной функции H(Z) построить схему ЦФ.

5) Выполнить нужные расчеты по учету эффекта конечных разрядностей.

Недостаток метода в том, что преобразование частот носит нелинейный характер. Метод применяется, в основном, при проектировании частотно–селективных фильтров.

Пример:

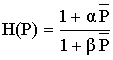
Решение: определим H(Z) подстановкой