5.1. Классификация радиотехнических цепей
5.2. Характеристики линейных радиотехнических цепей
5.3. Инерционные линейные цепи
5.4. Методы анализа преобразования сигналов линейными цепями
5.5. Простейшие радиотехнические цепи
5.5.1. Пассивные апериодические цепи
5.1. Классификация радиотехнических цепей
При рассмотрении обобщённой структурной схемы радиотехнической информационной системы было показано, что передача сообщений сопровождается цепочкой преобразований сигналов. Преобразования сопровождаются различными радиотехническими устройствами, которые представляют собой совокупность физических объектов, между которыми существуют определённые взаимодействия. Отдельный объект, осуществляющий то или иное преобразование сигналов, называется радиотехнической цепью.
Радиотехническая цепь имеет вход, на который подаётся исходный сигнал, и выход, откуда снимается преобразованный сигнал. Такая цепь как физическая система является одномерной. Если цепь имеет несколько входов и выходов, то она называется многомерной. В дальнейшем будут рассматриваться только одномерные системы.
Если неизвестны внутренние процессы преобразования сигналов, то радиотехническую цепь можно представить в виде т.н. “чёрного ящика” (рис. 5.1), где 
оператор преобразования. Вместе с тем, в ряде случаев рассматривают и внутренние состояния радиотехнической цепи. К характеристикам состояния можно отнести напряжения и токи на различных элементах(резисторах, емкостях, индуктивностях) цепи. Если цепь характеризуется только одним состоянием, то она называется цепью первого порядка. Если же в качестве состояний рассматриваются токи или напряжения на n элементах цепи, то цепь является цепью n-го порядка. Порядок цепи оказывает существенное влияние на вид оператора преобразования 
.
Таким образом, результат преобразования входного сигнала радиотехнической цепью с оператором можно записать следующим образом
(5.1)
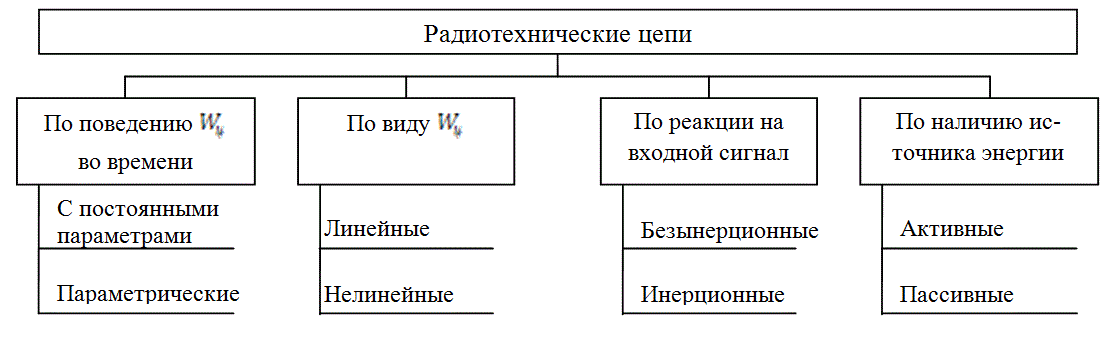
Рис. 5.2
Это обобщённое выражение позволяет провести классификацию радиотехнических цепей (рис. 5.2).
В первую очередь, отметим, что оператор преобразования с течением времени может оставаться постоянным, либо изменяться. Поскольку оператор преобразования целиком определяется параметрами цепи, то очевидно, неизменный во времени оператор характеризуется постоянными параметрами и цепи называются цепями с постоянными параметрами. Если же оператор 
изменяется во времени, то выходной сигнал описывается выражением
, (5.2)
а цепь называется цепью с переменными параметрами или параметрической цепью.
По виду оператора преобразования цепи делятся на линейные и нелинейные. Если оператор удовлетворяет условиям
, (5.3)
, (5.4)
то он является линейным оператором и цепь соответственно является линейной. В противном случае цепь относится к нелинейным цепям.
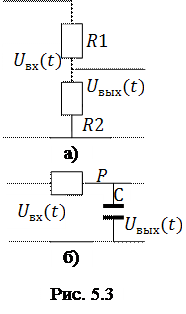
Условия (5.3) и (5.4) отражают фундаментальный принцип суперпозиции, который состоит в том, что реакция, т.е. выходной отклик цепи на сумму сигналов равен сумме откликов на эти сигналы, поступившие на вход цепи по отдельности. Простейшие линейные цепи (резисторный делитель напряжения и RC-цепь) изображены на рис. 5.3. Если выходной сигнал радиотехнической цепи в некоторый момент времени 
определяется только значением входного сигнала в тот же момент времени, то такая цепь называется безынерционной. Если же выходной сигнал зависит не только от значения входного сигнала в данный момент времени 
, но и от значений в предыдущие моменты времени, то такая цепь является инерционной. Очевидно, резисторный делитель (рис. 5.3, а) является безынерционной. Инерционность цепи определяется наличием в её составе ёмкостей и индуктивностей, поэтому RC-цепь, изображённая на рис. 5.3, б является инерционной цепью.
Завершим классификацию цепей по признаку наличия в составе цепи источника энергии. Если источник энергии в составе цепи отсутствует, такая цепь называется пассивной. Приведённые выше линейные цепи являются пассивными. При наличии же источника энергии в составе цепи цепь является активной. В качестве активных элементов радиотехнических цепей выступают электронные лампы, транзисторы и т.д. С этой точки зрения усилитель электрических сигналов является активной цепью.
5.2. Характеристики линейных радиотехнических цепей
При рассмотрении радиотехнических сигналов было установлено, что сигнал может быть представлен как во временной (динамическое представление), так и в частотной (спектральное представление) областях. Очевидно, при анализе процессов преобразования сигналов цепи также должны иметь соответствующие описания временными или частотными характеристиками.
Начнём с рассмотрения временных характеристик линейных цепей с постоянными параметрами. Если линейная цепь осуществляет преобразование в соответствии с оператором и на вход цепи подаётся сигнал 
в виде дельта-функции (на практике очень короткий импульс), то выходной сигнал (реакция цепи)
(5.5)
называется импульсной характеристикой цепи. Импульсная характеристика составляет основу одного из методов анализа преобразования сигналов, который будет рассмотрен ниже.
Если на вход линейной цепи поступает сигнал 
, т.е. сигнал вида “единичный перепад”, то выходной сигнал цепи
(5.6)
называется переходной характеристикой.
Между импульсом и переходной характеристикой существует однозначная связь. Так как дельта-функция (см. подраздел 1.3):
,
то подставляя это выражение в (5.5), получим:
. (5.7)
В свою очередь переходная характеристика
. (5.8)
Перейдём к рассмотрению частотных характеристик линейных цепей. Применим к входному 
и выходному 
сигналам прямое преобразование Фурье
,
.
Отношение комплексного спектра выходного сигнала к комплексному спектру входного сигнала называется комплексным коэффициентом передачи
(5.9)
Из этого следует, что
. (5.10)
Таким образом, оператором преобразования сигнала линейной цепью в частотной области служит комплексный коэффициент передачи.
Представим комплексный коэффициент передачи в виде
, (5.11)
где 
и 
соответственно модуль и аргумент комплексной функции 
. Модуль комплексного коэффициента передачи 
как функция частоты называется амплитудно-частотной характеристикой (АЧХ), а аргумент 
– фазочастотной характеристикой (ФЧХ). Амплитудно-частотная характеристика является чётной, а фазочастотная характеристика – нечётной функцией частоты 
.
Врменные и частотные характеристики линейных цепей связаны между собой преобразованием Фурье
, (5.12)
, (5.13)
что вполне объяснимо, поскольку они описывают один и тот же объект – линейную цепь.
5.3. Инерционные линейные цепи
Как уже отмечалось ранее, если выходной сигнал цепи определяется не только значениями входного сигнала в рассматриваемый момент времени , но и значениями входного сигнала в предыдущие моменты, то такая цепь называется инерционной. Если к этому же оператор преобразования линейный, то радиотехническая цепь является линейной инерционной цепью.
Линейные инерционные цепи (их ещё называют динамическими) нашли широкое распространение в радиотехнике. К ним относятся простейшие RC и RL цепи, колебательные контура и т.д. Как правило, линейные инерционные цепи описываются линейными дифференциальными уравнениями.
В качестве примера рассмотрим простейшую RC-цепь, изображённую на рис. 5.3, б. Согласно закону Кирхгофа можно записать
, (5.14)
где 
и 
- напряжения на соответствующих элементах цепи. Но напряжение является выходным сигналом цепи, т.е. 
. С другой стороны, напряжение на резисторе
,
где 
– ток, протекающий в цепи. Так как в цепь включена ёмкость, то ток протекающий в цепи:
,
.
Подставляя эти выражения в выражение (5.14), получим:
. (5.15)
Таким образом, простейшая RC-цепь описывается линейным дифференциальным уравнением первого порядка. Отметим, что состояние цепи характеризуется только напряжением на ёмкости, поэтому данная цепь является цепью первого порядка. Отсюда следует, что порядок дифференциального уравнения соответствует порядку цепи.
В общем случае линейная инерционная цепь описывается линейным дифференциальным уравнением n-ого порядка
(5.16)
или в компактной записи
, (5.17)
где 
и 
- коэффициенты уравнения.
Если известно дифференциальное уравнение (5.16), описывающее линейную цепь, можно найти характеристики цепи. Применим к обеим частям уравнения (5.16) прямое преобразование Фурье. Тогда, с учётом (2.47) можно записать
,
откуда следует
. (5.18)
Для рассмотренной выше RC-цепи уравнение (5.15) можно представить в виде
,
где 
, 
; 
.
Тогда комплексный коэффициент передачи цепи в соответствии с (5.18) будет иметь вид
Теперь, зная , можно определить импульсную характеристику, используя (5.13), а также переходную характеристику (5.8), АЧХ и ФЧХ цепи.
5.4. Методы анализа преобразования сигналов линейными цепями
Основной задачей анализа является определение реакции (выходного) сигнала цепи при действии на её входе сигнала известной формы. При этом, входной сигнал может быть описан как во временной, так и в частотной области. В связи с этим различают следующие методы анализа: классический, временной (или метод интеграла наложения), спектральный и операторный. Выбор того или иного метода зависит от структуры цепи, вида воздействующего на неё сигнала, формы представления (временная или частотная) входного сигнала.
5.4.1. Классический метод
Классический метод основывается на решении дифференциального уравнения вида (5.16), описывающего линейную цепь. Решение этого уравнения представляет собой сумму двух слагаемых
, (5.19)
где первое слагаемое представляет собой общее решение однородного дифференциального уравнения
, (5.20)
а второе слагаемое – частотное решение (5.16) при 
, где 
– правая часть уравнения (5.16). Физически 
– свободная составляющая полного отклика (выходного сигнала), представляет собой реакцию цепи на отключение(или включение) входного сигнала и характеризует переходные процессы в цепи. Второе слагаемое 
– вынужденная составляющая, является реакцией цепи после окончания переходных процессов и характеризует установившейся(стационарный) режим преобразования цепью входного сигнала. Обычно, классический метод используется для изучения переходных процессов, что приводит к необходимости решения уравнения (5.20). Общее решение однородного уравнения (5.20) имеет вид
, (5.21)
где 
, 
,…, 
– постоянные коэффициенты, определяемые начальными условиями,
, 
,…, 
– корни характеристического уравнения:
. (5.22)
Это уравнение имеет ровно n корней, при этом корни могут быть либо вещественными, либо комплексными, что определяет характер переходных процессов. Что же касается 
, то если входной сигнал является постоянным или периодическим, то после окончания переходных процессов выходной сигнал принимает форму входного сигнала. Так, если 
представляет собой гармонический сигнал, то также будет гармоническим, отличаясь от входного сигнала амплитудой и начальной фазой.
В качестве примера рассмотрим, что собой представляет отклик RC-цепи (рис. 5.3,8) на входной сигнал вида 
.
Дифференциальное уравнение цепи (5.15) перепишем в виде
,
где 
– постоянная времени.
Поскольку дифференциальное уравнение имеет порядок n=1, решение однородного уравнения
согласно (5.21), запишется в виде
,
где 
– корень характеристического уравнения
,
откуда следует 
. Тогда
.
До поступления входного сигнала ёмкость С разряжена. В момент 
поступления входного сигнала (скачка) ёмкость не может мгновенно зарядиться до 
, это произойдёт по мере перехода к установившемуся режиму. Очевидно в установившемся режиме
.
Таким образом, суммарный выходной сигнал
.
Коэффициент 
найдём из начальных условий. Начальными условиями при исследовании линейных цепей называют значения токов в индуктивностях и напряжений на емкостях в момент времени . Так как в этот момент времени 
, то можно записать
,
Откуда следует 
. Тогда окончательно суммарный выходной сигнал
.
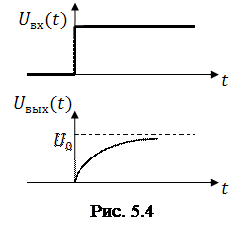
На рис. 5.4. изображены эпюры напряжений на входе и выходе исследуемой RC-цепи.
5.4.2. Временной метод
Временной метод (метод интеграла положения, метод интеграла Дюамеля) основывается на представлении входного сигнала цепи в виде суммы элементарных сигналов вида единичного скачка или очень короткого импульса ( 
– функции). Тогда, зная отклик линейной цепи на каждый элементарный сигнал и суммируя их можно получить в соответствии с принципом суперпозиции (наложения) полный отклик цепи на входной сигнал сложной формы.
Выберем в качестве элементарного сигнала – функцию. Тогда входной сигнал в соответствии с (1.19) можно записать следующим образом
.
Очевидно, выходной сигнал
.
Так как оператор не зависит от времени, его можно внести под знак интеграла. Тогда, с учётом (5.5)
. (5.23)
Если момент появления входного сигнала 
, то с учётом того, что выходной сигнал не может появиться ранее входного, выражение (5.23) принимает вид
. (5.24)
Таким образом, сигнал на выходе линейной цепи представляет собой свёртку входного сигнала с импульсной характеристикой цепи. Линейная цепь с постоянными параметрами при преобразовании проводит операцию взвешенного суммирования всех мгновенных значений входного сигнала, начиная с момента и заканчивая текущим моментом времени . Роль весовой функции выполняет импульсная характеристика цепи.
Выражение (5.24) носит название интеграла Дюамеля. Это выражение было получено в предположении, что входной сигнал представлен в виде суммы элементарных сигналов вида – функций. Если входной сигнал представить в виде (1.15) комбинаций сигналов вида единичного скачка, то можно получить другие формы интеграла Дюамеля, в частности
. (5.25)
Здесь 
– переходная характеристика цепи.
Итак, для использования метода интеграла наложения необходимо знать импульсную характеристику 
или переходную характеристику 
. Эти характеристики можно определить несколькими способами. Прямой (непосредственный способ состоит в решении дифференциального уравнения (5.20) в предположении, что входной сигнал является очень коротким импульсом(для определения импульсной характеристики) или сигналом вида единичного скачка( для определения переходной характеристики).
В выше приведённом примере было решено дифференциальное уравнение и найден отклик RC-цепи на воздействие сигнала
.
Очевидно, форма отклика не изменится, если входной сигнал будет единичным скачком, при этом масштаб отклика изменится в 
раз. Тогда выходной сигнал
, (5.26)
поскольку реакция цепи на единичный скачок является переходной характеристикой. В соответствии с (5.7) определяется импульсная характеристика
(5.27)
Второй способ определения импульсной или переходной характеристики, назовём его косвенным, состоит в использовании однозначного соответствия между импульсной характеристикой и комплексным коэффициентом передачи.
5.4.3. Спектральный метод
При рассмотрении характеристик линейной цепи было получено соотношение (5.10), связывающее спектральные характеристики входного и выходного сигнала с комплексным коэффициентом передачи цепи. Это соотношение лежит в основе спектрального анализа. Если задачей анализа является определение частотных характеристик выходного сигнала, то при известных 
и 
использование (5.10) полностью решает эту задачу. В ряде случаев сигнал представлен во временной области и требует найти отклик цепи как функцию времени. При этом использование метода интеграла наложения может быть затруднено сложностью нахождения импульсной характеристики цепи. В то же время комплексный коэффициент передачи найти достаточно просто. Тогда спектральный метод анализа сводится к следующим операциям:
- для входного сигнала прямым преобразованием Фурье находится комплексный спектр ;
- определяется комплексный коэффициент передачи цепи ;
- в соответствии с (5.10) определяется комплексный спектр выходного сигнала 
;
- обратным преобразованием Фурье вычисляется форма сигнала 
на выходе цепи.
Итак, важнейшим условием использования спектрального метода является знание комплексного коэффициента передачи исследуемой цепи. Найти комплексный коэффициент передачи можно, используя методы теории цепей (метод узловых потенциалов или метод контурных токов). Если известно аналитическое описание цепи дифференциальным уравнением (5.16), то комплексный коэффициент передачи находится в соответствии с (5.18). Наконец, цепь можно представить в виде делителя напряжения, элементами которого являются комплексные сопротивления
; 
; 
.
Проиллюстрируем последний подход на примере уже рассматривавшейся выше RC-цепи. Если представить цепь как делитель напряжения, то выходной сигнал представляет собой напряжение на ёмкости С. Тогда, если 
комплексный ток, протекающий в цепи, то
,
и комплексный коэффициент передачи
,
что совпадает с результатом, полученным в подразделе 5.3.
5.4.4. Операторный метод
Операторный метод является обобщением спектрального метода. В основе метода лежит преобразование Лапласа. Рассмотрим некоторый сигнал 
, определённый на интервале времени (0, 
). Умножим этот сигнал на 
и полученный новый сигнал 
подвергнем преобразованию Фурье
.
Обозначая через 
, получим
. (5.28)
Выражение (5.28) называется односторонним преобразованием Лапласа функции . При этом, называют оригиналом, а 
изображением.
Нетрудно убедиться, что при 
выражение (5.28) преобразуется к виду
,
что соответствует преобразованию Фурье. Таким образом если преобразование Фурье представляет собой спектральное разложение сигнала по гармоническим составляющим 
, то преобразование Лапласа – разложение сигнала по экспоненциально – косинусным составляющим 
. Действительно, представим
.
Здесь использована формула Эйлера
.
С другой стороны
,
где 
.
Тогда окончательно
представляет собой экспоненциально – косинусную функцию.
Переход от изображения 
к оригиналу осуществляется при помощи обратного преобразования Лапласа
. (5.29)
Для значительной части функций широко используемых при описании оригиналов были рассчитаны изображения по Лапласу. Некоторая часть оригиналов и изображений приведена в таблице 5.1.
Поскольку преобразование Лапласа является обобщением преобразования Фурье, то оно обладает теми же свойствами, что и преобразование Фурье. Остановимся на некоторых из них, которые будем использовать в дальнейшем. Пару преобразований (прямое и обратное) будем обозначать следующим образом
.
1. Линейность преобразований Лапласа
(5.30)
2. Свойство временного сдвига
(5.31)
3. Операция дифференцирования
; 
(5.32)
4. Операция интегрирования
. (5.33)
Применим к обеим частям уравнения (5.16) прямое преобразования Лапласа. Тогда с учётом (5.32), получим
(5.34)
откуда следует
. (5.35)
Это отношение называется передаточной функцией цепи или её операторным коэффициентом. Таким образом, передаточная функция является оператором преобразования линейной цепью в базисе экспоненциально – косинусных сигналов.
Сравним выражение комплексного коэффициента передачи (5.18) с выражением (5.35). Из этого сравнения следует, что комплексный коэффициент передачи является частным случаем 
при , т.е.
(5.36)
Таким образом, если известна передаточная функция цепи, то операторный метод поиска отклика цепи состоит в следующем:
- находится изображение по Лапласу входного сигнала
; (5.37)
- находится изображение выходного сигнала как произведение
; (5.38)
- определяется оригинал выходного сигнала
. (5.39)
Установим связь между временными характеристиками и передаточной функцией. Произведя в (5.12) замену 
на 
, получим
.
Таким образом, передаточная функция и импульсная характеристика связаны между собой преобразованием Лапласа
.
Что касается переходной характеристики, то применяя к (5.8) преобразование Лапласа и учитывая (5.33), получим
.
В заключение отметим, что операторный метод позволяет сводить линейные дифференциальные уравнения вида (5.16) к алгебраическим уравнениям (5.34), что позволяет в ряде случаев упростить анализ цепей. Помимо этого, учитывая широкое распространение таблиц преобразований Лапласа для большого числа функций, можно исключить громоздкие вычисления, непосредственно обращаясь к этим таблицам.
Рассмотрим применение операторного метода на примере анализа определения отклика RC-цепи на входной сигнал вида . Эта задача была решена классическими временными методами. Спектральным методом был найден комплексным коэффициент передачи. Заменив в выражении для цепи на , получим передаточную функцию цепи
.
Следуя операторному методу найдём изображение по Лапласу входного сигнала, воспользовавшись при этом таблицей 5.1
.
Далее, в соответствии с (5.38), определим изображение выходного сигнала
.
И наконец, по таблице 5.1 (позиция 5) находим оригинал
,
что совпадает с полученными ранее результатами.
5.5. Простейшие радиотехнические цепи
5.5.1. Пассивные апериодические цепи
При классификации радиотехнических цепей было отмечено, что по признаку наличия в цепи источника энергии цепи подразделяются на пассивные и активные. Начнем с рассмотрения пассивных цепей первого порядка, т.е. цепей содержащих один реактивный элемент (емкость или индуктивность). На основе этих цепей строятся как простейшие активные цепи, так и более сложные радиотехнические устройства.
Выше в качестве примера линейной цепи при рассмотрении методов анализа приводилась RC-цепь, которая получила название интегрирующей цепи. Рассмотрим еще одну RC-цепь, называемую дифференцирующей цепью, определим ее характеристики и сравним с характеристиками интегрирующей цепи.
Определение характеристик цепей можно проводить любым из рассмотренных выше методов. Так, например, при определении частотных характеристик цепей в данном случае удобно представить ту или иную цепь в виде делителя напряжения, в состав которого входят комплексные сопротивления 
и 
. Временные характеристики (переходную и импульсную) можно рассчитать как методом интеграла наложения, так и операторным методом.
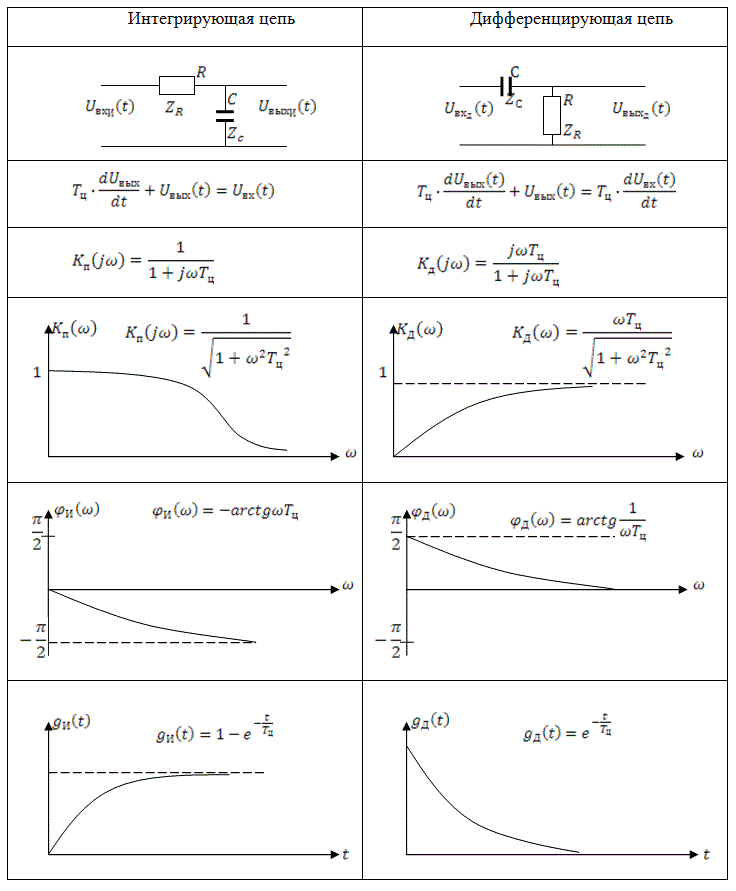
В таблице 5 представлены схемы интегрирующей и дифференцирующей цепи, дифференциальные уравнения, которыми описываются цепи, аналитические выражения комплексного коэффициента передачи 
, амплитудно-частотных 
, фазо-частотных 
, а также переходных 
и импульсных 
характеристик и их графические изображения.
Анализ графиков АЧХ цепей показывает, что интегрирующая цепь пропускает нижние частоты и задерживает верхние, т.е. является фильтром нижних частот (ФНЧ). Дифференцирующая цепь наоборот пропускает верхние частоты и тем самым является фильтром верхних частот (ФВЧ).
Форма временных (переходной и импульсной) характеристик определяет характер переходных процессов. Для рассматриваемых цепей переходные характеристики представляют собой монотонно возрастающую (для интегрирующей цепи) и монотонно убывающую (для дифференцирующей цепи) функции. Это определило название цепей как апериодических.
Обратимся к выражению для комплексного коэффициента передачи интегрирующей цепи. При 
комплексный коэффициент передачи
.
Так как входной и выходной сигналы связаны соотношением
,
то при указанном условии
. (5.40)
Но оператор 
является оператором интегрирования. Тогда применяя обратное преобразование Фурье, получим
,
т.е. цепь выполняет функцию интегрирования входного сигнала.
Аналогично для дифференцирующей цепи при 
и 
(5.41)
Таблица 5
Как известно, оператор 
– это оператор дифференцирования. Очевидно, обратное преобразование Фурье обеих частей (5.41) дает
.
Таким образом, рассмотренные простейшие RC-цепи осуществляют соответственно приближенное интегрирование и дифференцирование входных сигналов.
В заключение отметим, что в качестве интегрирующих и дифференцирующих цепей могут выступать и RL-цепи, где реактивными элементами являются индуктивности. Схемы этих цепей также представляют собой делители напряжения, с той лишь разницей, что в интегрирующей цепи выходной сигнал снимается с резистора, а в дифференцирующей – с индуктивности.
5.5.2. Пассивные частотно-избирательные цепи
К пассивным частотно-избирательным цепям относятся колебательные контуры. Простейший колебательный контур содержит резистор R, индуктивность L и емкость C. Если в контуре элементы R, L и C соединены последовательно, то такой контур называется последовательным, а если соединены параллельно – параллельным колебательным контуром.
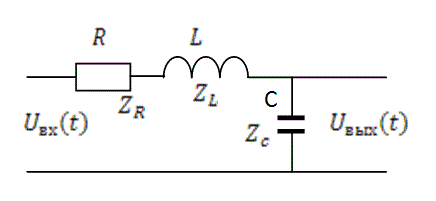
Рис.5.6
Один из вариантов последовательного колебательного контура изображен на рис. 5.6. Так же, как и предыдущие цепи, рассматриваемый контур можно представить как делитель напряжения. Тогда
комплексный коэффициент передачи контура
,
или с учетом того, что 
, 
и 
:
. (5.42)
Из этого выражения следует, что комплексный коэффициент передачи имеет максимум при
, (5.43)
т.е. последовательный колебательный контур из совокупности сигналов разных частот выделяет один, который имеет частоту 
. Это явление, как известно, называется резонансом, а частота 
– резонансной частотой.
Резонансная частота определяется из условия (5.43):
или 
. (5.44)
Рассмотрим основные характеристики последовательного колебательного контура.
Характеристическим сопротивлением называется значение сопротивления одного из реактивных элементов (индуктивности или емкости) при резонансной частоте
. (5.45)
Добротностью контура называется отношение характеристического сопротивления к резистивному
. (5.46)
Поясним физический смысл добротности. Из (5.42) при имеем
.
Тогда с учетом (5.46) можно записать
. (5.47)
Таким образом, добротность показывает во сколько раз напряжение на индуктивности или емкости (выходной сигнал) больше, чем приложенное входное напряжение. Затуханием контура называется безразмерная величина, обратная добротности
.
Постоянная времени контура
, (5.48)
характеризует инерционность контура. Очевидно, чем больше 
(чем больше 
), тем медленнее протекают переходные процессы в контуре.
Возвратимся к (5.42) и представим это выражение с учетом (5.44) в виде
.
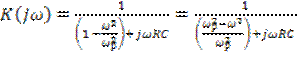Обозначая
,
после несложных преобразований получим
.
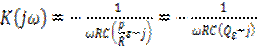Рассмотрим поведение комплексного коэффициента передачи в окрестности резонансной частоты, т.е. при 
. Тогда величина 
:
, (5.49)
где 
– абсолютная расстройка, представляет собой так называемую удвоенную относительную расстройку. С учетом этого выражение для комплексного коэффициента передачи можно представить как функцию удвоенной относительной расстройки в следующем виде
. (5.50)
Амплитудно-частотная характеристика
, (5.51)
а фазо-частотная характеристика
. (5.52)
На рис. 5.7 изображены графики АЧХ и ФЧХ рассматриваемого колебательного контура в окрестности резонансной частоты.
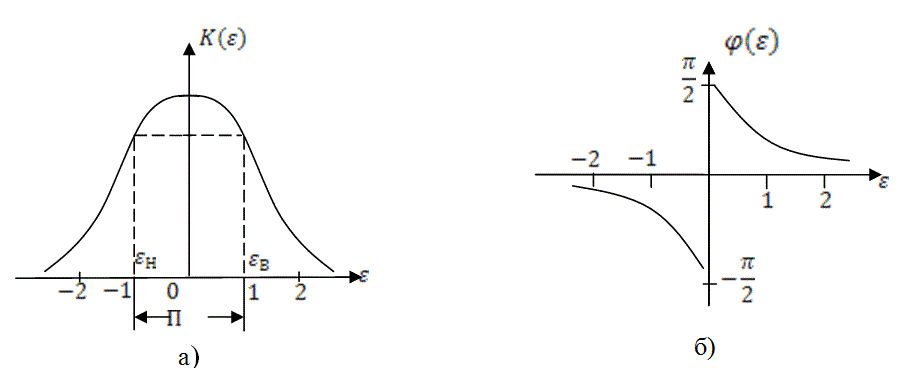
Рис. 5.7
Полосой пропускания контура называется диапазон частот, в пределах которого 
. Очевидно, равенство в этом выражении соответствует граничным частотам 
и 
полосы пропускания. Эти частоты находятся в результате решения уравнения
. (5.53)
Решение этого уравнения дает
, 
,
или с учетом (5.49)
, 
.
Тогда полоса пропускания контура определяется по формуле
. (5.54)
В заключение составим дифференциальное уравнение последовательного колебательного контура. Напряжение, приложенное к контуру:
, (5.55)
где 
– напряжение на резисторе, 
– напряжение на индуктивности, 
– напряжение на конденсаторе. Но напряжение на конденсаторе является выходным сигналом 
. С другой стороны напряжение на резисторе 
, а напряжение на индуктивности 
. Ток, протекающий через контур, можно выразить через напряжение на конденсаторе
.
Тогда напряжение на индуктивности
,
и на резисторе
.
Подстановка этих выражений в (5.55) дает соотношение
.
Разделим обе части этого уравнения на 
. Тогда уравнение принимает вид
, (5.56)
где 
– коэффициент затухания.
Применив к обеим частям уравнения (5.56) преобразование Лапласа, можно получить выражение для передаточной функции
. (5.57)
Нетрудно заметить, что замена в (5.57) 
на приводит к выражению (5.42).
Параллельный колебательный контур представляет собой параллельное соединение 
, 
и 
элементов (рис. 5.8). Входным сигналом такого контура является ток 
, а выходным – напряжение 
на элементах контура. Согласно закону Ома комплексное значение напряжения на элементах контура
.
В свою очередь комплексное сопротивление 
есть величина, обратная комплексной проводимости. При параллельном соединении 
, 
и 
комплексная проводимость равна
, (5.58)
или
. (5.59)
Проводя суммирование дробей, и вычисляя обратное значение суммы, получим
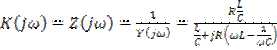. (5.60)
Как и в последовательном контуре, резонанс в параллельном колебательном контуре, как это следует из (5.60), имеет место при условии 
.
Характеристическое сопротивление контура описывается выражением (5.45). Что касается добротности 
, то в отличие от (5.46) для параллельного контура она определяется выражением
. (5.61)
Отсюда постоянная времени контура
. (5.62)
Вводя параметр 
и проводя аналогичные рассуждения, как и в случае последовательного контура, после несложных преобразований получим выражение для 
в окрестности резонансной частоты:
. (5.63)
Очевидно, амплитудно-частотная характеристика
, (5.64)
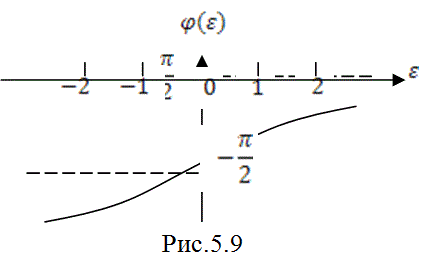
носит такой же характер, как и для последовательного контура (5.51). Поэтому график АЧХ параллельного контура совпадает по форме с кривой рис. 5.7а. Фазо-частотная характеристика имеет вид
. (5.65)
На рис. 5.9 приведен график ФЧХ параллельного контура. Полоса пропускания и граничные частоты 
и 
определяются аналогично этим же параметрами последовательного контура. При составлении дифференциального уравнения следует учесть, что входной сигнал – ток
, (5.66) где 
; 
; 
– токи, протекающие через соответствующие элементы, 
– напряжение на контуре, являющееся выходным сигналом 
.
Подстановка этих выражений в (5.65) дает
.
Дифференцирование левой и правой частей приводит к результату
, (5.67)
где 
– коэффициент затухания.
Передаточная функция параллельного контура описывается выражением
. (5.68)
5.5.3. Активные линейные цепи
Типичным примером активной цепи является усилитель, собранный на n-p-n транзисторе с общим эмиттером. Если нагрузкой усилителя служит R-цепь, то такой усилитель является апериодической активной цепью, а если нагрузкой служит колебательный контур – частотно-избирательной активной цепью.
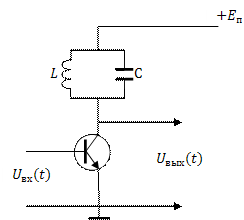
Рис. 5.10
На рис. 5.10 представлена упрощенная принципиальная схема частотно-избирательной активной цепи. При достаточно малой амплитуде входного сигнала такую цепь можно считать линейной (линейным усилителем малых сигналов). Этот случай мы и рассмотрим.
Для определения характеристик рассматриваемой активной цепи составим ее эквивалентную схему. Транзистор можно представить в
виде источника тока управляемого напряжением 
. Величина тока в этом случае составит
, (5.69)
где 
– крутизна характеристики транзистора (крутизна управления), имеющая размерность 
. Как известно, источник тока можно представить как параллельное соединение идеального источника и внутреннего сопротивления, в качестве которого выступает внутреннее сопротивление транзистора 
. Тогда эквивалентная схема рассматриваемой цепи принимает вид (рис. 5.11).
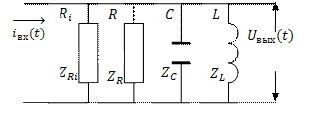
Рис.5.11
Так же, как и для пассивной цепи (параллельного контура) комплексный коэффициент передачи:
.
совпадает с комплексным сопротивлением 
. Вместе с тем, для рассматриваемой цепи комплексная проводимость определяется выражением
, (5.70)
где 
– эквивалентное сопротивление контура с учетом внутреннего сопротивления транзистора. Сравнение (5.70) с (5.59) показывает, что комплексный коэффициент передачи рассматриваемой цепи описывается выражением (5.60) с той лишь разницей, что вместо собственного сопротивления параллельного контура 
здесь выступает 
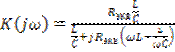. (5.71)
Очевидно, исходя из эквивалентной схемы, добротность рассматриваемого усилителя составит величину
. (5.72)
Так как 
, то включение параллельного контура в качестве нагрузки усилителя приводит к уменьшению его добротности, что объясняется шунтирующим свойством транзистора.
Аналогично комплексный коэффициент передачи как функция удвоенной относительной расстройки ε описывается выражением
, (5.73)
а амплитудно-частотная и фазо-частотная характеристики – соответственно выражениями:
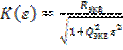, (5.74)
. (5.75)
Полоса пропускания рассматриваемого усилителя определяется в соответствии с (5.54), где вместо фигурирует 
. (5.76)
Очевидно, так как включение параллельного контура в качестве нагрузки усилителя приводит к уменьшению его добротности до , это в свою очередь обуславливает расширение полосы пропускания.