Характеристики системы связи в значительной степени зависят от параметров канала связи, который используется для передачи сообщений. Исследуя пропускную способность каналов, мы предполагали, что их параметры сохраняются постоянными. Однако большинство реальных каналов обладают переменными параметрами. Параметры канала, как правило, изменяются во времени случайным образом. Как уже отмечалось (§ 5.7), случайные изменения коэффициента передачи канала μ вызывают замирания сигнала, что эквивалентно воздействию мультипликативной помехи. Эквивалентная мощность этой помехи согласно (5.76) равна Тогда суммарная мощность помех в канале с переменными параметрами при наличии аддитивной помехи будет равна:

Отсюда следует, что замирания сигнала приводят к увеличению мощности помех, а следовательно, и к снижению пропускной способности канала (6.87) .

Рассмотрим, каким образом вычисляется пропускная способность канала с замираниями при передаче непрерывных сообщений. В этих условиях необходимо найти такое распределение вероятностей сигнала, которое при заданных статистических свойствах коэффициента передачи μ обеспечивало бы максимальную скорость передачи информации.

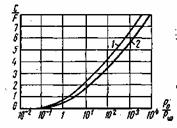
Рис. 6.5. Зависимость пропускной способности от среднего отношения сигнала к помехе для каналов с постоянными параметрами (1) и рэлеевскими замираниями (2)

Решение задачи в общем виде вызывает значительные трудности. Однако в случае медленных замираний, когда скорость замираний намного меньше скорости изменения непрерывного сообщения, можно с достаточной точностью предсказывать по текущим значениям коэффициента его последующие значения. При таком допущении максимум скорости передачи по-прежнему имеет место для сообщений с нормальным распределением, что дает возможность пользоваться ф-лой (6.87). Подставляя в (6.87) мощность принимаемого сигнала ²Р0, где Р0—переданная мощность сигнала, получим пропускную способность при фиксированном :

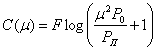
Усреднив по всем значениям , найдем среднее значение пропускной способности канала при медленных замираниях

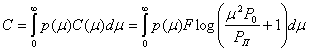
где p() — плотность вероятности коэффициента передачи. Во многих каналах изменения коэффициента подчиняются закону Рэлея (5.77). На рис. 6.5 показаны зависимости C/F от среднего отношения Р/Рдля канала с постоянными параметрами 1 и канала с рэлеевскими замираниями 2. Из анализа кривых рис. 6.5 следует, что медленные рэлеевеские замирания уменьшают пропускную способность канала не более чем на 17%.

Для вычисления пропускной способности дискретных каналов при быстрых замираниях могут быть использованы выражения для С, полученные при постоянных параметрах (6.58) и (6.59). В эти формулы необходимо подставить вместо вероятности ошибки ее среднюю статистическую величину, найденную путем усреднения по всем значениям коэффициента . Подставляя (5.81) в (6.58), получаем выражение для пропускной способности канала с ортогональными двоичными сигналами ири быстрых рэлеевских замираниях

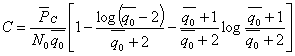
Здесь - что дает возможность заменить в (6.58)

отношением

Полученное выражение для С обладает максимумом, который достигается при :

В этом случае наблюдается значительный проигрыш по сравнению с пропускной способностью аналогичного канала без замираний

В многопозиционных системах положение существенно улучшается. Если число позиций , то при рэлеевских замираниях

Это дает проигрыш всего лишь на 27% по сравнению с таким же каналом без замираний. Отсюда следует вывод, что в условиях замираний передача дискретных сообщений более эффективна при использовании многопозиционных кодов.