2.1. Технологические процессы как объекты управления

2.2. Устройства получения информации

2.3. Преобразование исходных сигналов датчиков

2.4. Аналого-цифровые и цифро-аналоговые преобразователи

2.1. Технологические процессы как объекты управления

Технологические процессы представляют собой первичное звено создания материальных ценностей, обеспечивающее производство необходимой для общества продукции. Во всех технологических процессах происходит преобразование или перенесение материалов, энергии и информации.

Технологические процессы как объекты управления можно поделить на следующие группы:

непрерывные технологические объекты, в которых перемещение материалов, энергии и информации происходит в виде потоков, обеспечивающих непрерывное функционирование объекта (в химической, газовой, нефтехимической промышленности, в энергетике и т.п.);

непрерывно-дискретные технологические объекты, в которых процессы протекают в ограниченном времени, а перемещение материалов, энергии и информации происходит в виде непрерывных потоков (в металлургии и химической промышленности, например, вулканизации, полимеризации);

дискретные технологические объекты, которые характеризуются однократным протеканием процессов и перемещением материалов, энергии, информации в виде отдельных элементов (в машиностроении при изготовлении деталей).

Для того чтобы представить технологический процесс как объект управления, необходимо абстрагироваться от конкретных физических, химических или технологических условий, их характеристик, определяющих условия протекания технологических процессов. Это необходимо для создания общих принципов и методов представления объекта в теории управления независимо от разной природы объектов. При этом конкретные особенности каждого объекта должны учитываться при разработке его математической модели, способов получения информации от объекта и вывода управляющих воздействий на объект.

Рассмотрим технологический процесс в виде многомерного объекта (рис. 2.1).

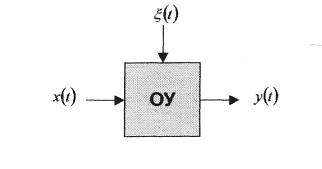
Рисунок 2.1. Схема многомерного объекта

К входным переменным Х(t)={Х₁(t),...,Х_n(t)} относятся параметры сырья и теплоносителей (давление, температура, химический состав, концентрация), а также параметры разных компонентов, которые принимают участие в протекании технологического процесса (температура, давление, например, воздуха, воды и инертного газа).

К выходным переменным Y(t) = {Y₁(t),...,Y_n(t)} можно отнести параметры выходного продукта (химический состав, размеры, концентрацию), режимные параметры объекта (температуру и давление продукта на выходе), технико-экономические показатели объекта (производительность, коэффициент полезного действия, себестоимость, затраты сырья). На технологические объекты действуют измеряемые и неизмеряемые возмущения, которые характеризуют условия протекания процесса

. (2.1)

К этим переменным относятся температура и влажность окружающей среды, наличие примесей в исходном сырье, а также параметры, которые определяют состояние объекта (активность катализатора, кристаллизация на внутренних стенках трубопроводов и т.д.). Значение переменных Y(t) зависит от входных переменных Х(t) и возмущений . В качестве управляющих воздействий может применяться часть входных переменных. При создании системы управления невозможно учитывать все переменные, которые влияют на ход технологического процесса. Поэтому в системе управления принимают участие только основные переменные, прежде всего те, которые определяют ход процесса.

При рассмотрении технологического процесса как объекта управления необходимо:

• изучить технологическую схему;
• представить технологический процесс в виде некоторого числа систем, связанных между собой материальными потоками;
• получить приближенные оценки статистических параметров материальных потоков с целью отбора существенных параметров для дальнейшего создания математической модели и разработки системы управления.

Для математического описания сложного объекта автоматического управления наиболее совершенными являются экспериментально-статистические методы. Аппарат корреляционного и регрессивного анализов разрешает получить математическое описание объекта в виде полинома. Эта зависимость называется уравнением регрессии. Для накопления статистического материала используются активный и пассивный эксперименты. Лучшие результаты в построении регрессивных статистических моделей достигаются при проведении активного эксперимента.

Активный эксперимент базируется на использовании искусственных возмущений, которые вводятся в объект по ранее спланированной программе.

Математическое описание технологического процесса в статике можно представить в виде полинома (уравнения регрессии):

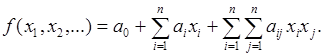(2.2)

Для определения коэффициентов регрессии линейной модели используются ортогональные экспериментальные планы.

План эксперимента на двух уровнях строится таким образом, чтобы в каждом эксперименте одновременно изменялись все значения относительно начальных базовых значений. При этом каждая переменная X в интервале варьирования может принимать только два крайних значения:

(2.3)

и обозначаться +1 и -1. Переход от нормализованных значений к кодовым определяется по формуле

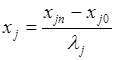, (2.4)

где х_j0 - базовое значение переменной;

- шаг варьирования.

С помощью эксперимента на двух уровнях можно получить линейную статистическую модель объекта вида

(2.5)

где - оценки коэффициентов регрессии.

Планирование эксперимента проводят с помощью матрицы планирования, которую составляют по правилам, изложенным ниже после табл.2.1.

Таблица 2.1. Матрица планирования

g	X0	x1	x2	x3	x1 x2	x1 x3	x2 x3	x123
1	+1	-1	-1	-1	+1	+1	+1	-1
2	+1	+1	-1	-1	-1	-1	+1	+1
3	+1	-1	+1	-1	-1	+1	-1	+1
4	+1	+1	+1	-1	+1	-1	-1	-1
5	+1	-1	-1	+1	+1	-1	-1	+1
6	+1	+1	-1	+1	-1	+1	-1	-1
7	+1	-1	+1	+1	-1	-1	+1	-1
8	+1	+1	+1	+1	+1	+1	+1	+1

В первой строке все управляющие факторы выбирают на нижнем уровне. Последующие варианты строят так, чтобы при переборке всех вариантов частота изменения знака фактора х_і+1 была в два раза меньше, чем для предыдущего. Три столбца х₁,х₂,х₃ соответственно создают матрицу, а другие столбцы получают перемножением соответствующих значений управляющих факторов и необходимых для расчета соответствующих коэффициентов.

Проведение эксперимента. Так как значение ответа Y носит случайный характер, то в каждой точке X_g проводят m параллельных опытов и находят среднее значение результатов исследований

. (2.6)

Перед реализацией плана на объекте необходимо рангомизировать варианты варьирования, т.е. с помощью таблицы равномерно распределенных случайных чисел определить последовательность реализации вариантов варьирования.

Проверка воспроизведения эксперимента представляет собой проверку гипотезы о равенстве генеральных дисперсий

(2.7)

Оценки дисперсии определяются из формулы

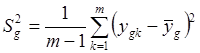. (2.8)

Для проверки гипотезы об однородности оценок пользуются критерием Кохрена

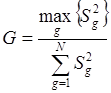. (2.9)

Если полученное значение критерия G окажется меньше критического G_kp, найденного из таблицы, то гипотеза принимается, а если нет, то нужно увеличить число параллельных опытов.

Получение математической модели

Оценки коэффициентов находятся согласно формулам:

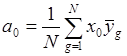, (2.10)

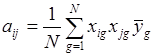, (2.11)

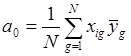. (2.12)

После определения оценок коэффициентов регрессии необходимо проверить гипотезы об их значимости с помощью критерия Стьюдента:

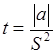, (2.13)

где S - дисперсия оценки коэффициента.

Если Sign(t-t_kp)= +1 - оценку признают значимой.

Если Sign(t-t_kp)= -1 - = 0.

Проверку адекватности математического описания проводят согласно F - критерию Фишера

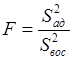. (2.14)

Если F<F_kp, найденного из таблицы, то гипотезу не отвергают. В противном случае математическое описание признается неадекватным и необходимо перейти к более сложной форме математического описания или проводить эксперимент с меньшим интервалом варьирования.

, (2.15)

где d - число членов полинома;

- предусмотренная величина ответа из полученного уравнения регрессии.

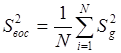. (2.16)

Интервал варьирования можно выбрать равным 0.05 - 0.3 от возможного диапазона варьирования факторов, т.е. область варьирования составляет 10-60% от всего диапазона. Начальную точку варьирования выбирают как можно ближе к центру области факторного пространства.

2.2. Устройства получения информации

Устройства получения информации предназначены для сбора и преобразования информации без изменения ее содержания о контролирующих и управляющих параметрах технологических процессов. К устройствам получения информации о состоянии процесса относятся чувствительные элементы или датчики, измерительные и нормирующие преобразователи. К этой же группе устройств относятся релейные (позиционные) преобразователи.

Измерительный преобразователь это совокупность чувствительного элемента, измерительного и нормирующего преобразователей. Нормирующие
преобразователи переводят выходной сигнал измерительного преобразователя с естественным выходом в унифицированный сигнал.

В настоящее время наиболее распространенные выходные сигналы: величины постоянного и переменного токов, напряжения, импульсы, модулированные по амплитуде, ширине, фазе или частоте и давление воздуха. Величины основных унифицированных сигналов установлены соответствующими стандартами и приведены в табл. 2.2.

Таблица 2.2. Унифицированные сигналы преобразователей

Для организации введения данных из датчиков необходимо осуществить опрос датчиков и определить значение измеряемых величин согласно показателям датчиков. Режим получения данных с объекта управления реализуется с помощью циклического и адресного опроса датчиков. При циклическом опросе датчики периодически опрашиваются в предварительно заданной и установленной последовательности. При этом в каждом цикле (такте квантования) отдельные датчики опрашиваются несколько раз через промежутки времени . Результаты опросов усредняются, и средние значения запоминаются. После этого через промежуток времени, который равен периоду квантования , весь процесс повторяется, т.е. датчики снова опрашиваются раз с дискретностью , и результаты опроса усредняются. Для большей точности желательно, чтобы при ограничении .

При адресном опрашивании по адресу, указанному оператором или определенному автоматически, опрашивается один или несколько датчиков. Для использования результатов опрашивания в алгоритмах управления необходимо определить истинные значения измерительных величин согласно показателям датчиков. Исходный сигнал датчика с истинным значением измерительного параметра X в общем случае заменяется нелинейной зависимостью вида . Для определения измерительной величины X по показателям датчика разработано много алгоритмов.

При линейной характеристике датчика значение измерительной переменной определяется следующим образом

, (2.17)

где - нижняя и верхняя границы шкалы измерительного параметра;

- нижняя и верхняя границы выходных сигналов датчика;

х - текущее значение параметра X;

у - выходной сигнал датчика текущего значения параметра х при каждом опросе.

При квадратичной характеристике датчика значения параметра определяются формулой

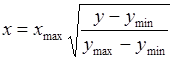. (2.18)

Если зависимость У от Х аналитически определить невозможно, то для определения истинного значения измеряемого параметра используются аппроксимирующие полиномы

, (2.19)

где - постоянные коэффициенты, которые определяются таким образом, чтобы погрешность аппроксимации (2.19) не превышала допустимого значения во всем интервале измеряемого параметра и сигнала , полученного с датчика.

Оценка точности представления сигналов. Реальный физический сигнал , снимаемый с выхода датчика, превращается в соответствующий цифровой код. Связь между реальным сигналом и точным невозбужденным значением сигнала на выходе датчика может быть представлена в виде

, (2.20)

где - погрешность, которая вызвана несовершенством динамической характеристики датчика;

- высокочастотный низкого уровня шум на выходе датчика;

- возможные сбои в работе датчика;

- случайная помеха, которая обусловлена дрейфом коэффициентов характеристики датчика в результате старения и других причин.

Влияние высокочастотной помехи может быть уменьшено применением алгоритмов усреднения, которые реализуют функции выделения постоянной составляющей сигнала в реальном времени и фильтрации случайных выбросов.

Для реализации фильтров высокочастотных помех применяется алгоритм усреднения с бесконечной памятью. Допустим, что на сигнал постоянной величины накладывается случайная помеха так, чтобы измерительный сигнал, который снимается с датчика, был равен

. (2.21)

Определим значение постоянного сигнала по методике наименьших квадратов

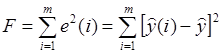. (2.22)

Благодаря минимизации функции потерь из условия 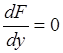, получаем усредненную оценку

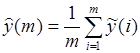. (2.23)

Алгоритм усреднения в рекурентной форме получается путем вычитания предыдущей оценки из (2.23):

. (2.24)

Рассмотренный алгоритм не применяется для оценки сигнала , который изменяется медленно. В этом случае применяется алгоритм усреднения с ослабленной памятью. В предыдущем алгоритме предусматривалось, что оцениваемая координата в интервале измерений остается постоянной. В этом случае в отдельные измерения входят значения с одинаковыми весами, независимые от дискретного времени . Если нужно отследить медленно изменяющийся сигнал , то новым измерениям необходимо увеличить вес сравнительно с теми, которые были получены раньше. Усредненная оценка параметра

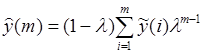, (2.25)

где величина выбирается порядка 0.95.

Алгоритм усреднения получим в виде

, (2.26)

где - усредненное значение сигнала , снимаемого с датчика.

Для устранения применяют алгоритмы перехода контролирующего параметра за допустимые границы. Простейший алгоритм базируется на отбраковке следующего опрошенного сигнала при выходе его за известный диапазон изменения . Если известная погрешность сигнала и диапазон изменения , то значение сигнала при -м опросе бракуется, если для него не выполняется условие

. (2.27)

При этом заменяют предыдущим по времени небракованным значением сигнала . Более тщательное устранение сбоев выполняется с учетом диапазона и скорости изменения при известной погрешности сигнала . При этом сигнал бракуется, если не выполняется хотя бы одно из неравенств:

(2.28)

. (2.29)

При преобразовании в АЦП аналогового сигнала в цифровой код возникает погрешность округления, которая равняется половине последнего верного разряда кода числа, которую условно можно отнести к составной .

2.3. Преобразование сигналов датчиков

Процесс преобразования аналоговых сигналов в цифровые, кроме процедуры преобразования, включают в себя операции обработки аналоговых сигналов, определенных условиями заданного качества сигнала, а в отдельных случаях необходимостью проведения функцио-нальных преобразований.

Большинство датчиков имеют большое исходное сопротивление и малый динамический диапазон, поэтому необходимо согласование выходных параметров датчиков с параметрами входных цепей системы обработки данных. В качестве устройств согласования чаще всего применяются операционные усилители, которые представляют собой усилители постоянного тока с большим коэффициентом усиления (например, ).

Рассмотрим основные схемы включения операционных усилителей: инвертирующий усилитель (рис. 2.2.) и неинвертирующий усилитель (рис.2.3).

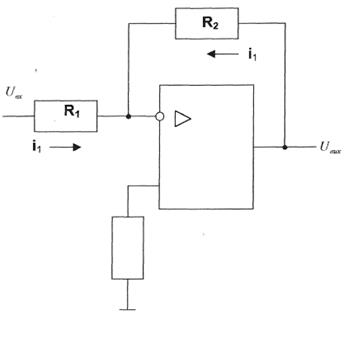
Рисунок 2.2. Инвертирующий усилитель

Перед анализом схемы вспомним основные правила:

• выход операционного усилителя стремится достичь такого состояния, чтобы разность напряжений между его входами была равна 0;
• входы операционного усилителя тока не потребляют.

Согласно первому и второму законам Кирхгофа можно записать

, (2.30)

тогда коэффициент усиления по напряжению для схемы инвертирующего усилителя

. (2.31)

Недостатком схемы является то, что она имеет малый входной импеданс. Этот недостаток устраняет схема неинвертирующего усилителя (рис. 2.3), для которого

, (2.32)

отсюда коэффициент усиления по напряжению

. (2.33)

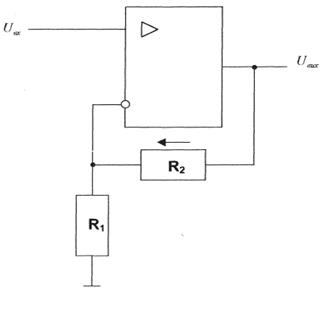
Рисунок 2.3. Неинвертирующий усилитель

Схема усилителя с единичным коэффициентом усиления (повторителя напряжения) приведена на рис.2.4.

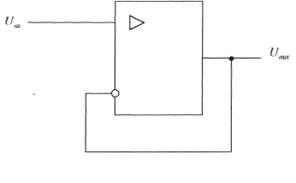
Рисунок 2.4. Повторитель напряжения

Такой усилитель также называют буфером, так как он имеет изолирующие свойства (большой входной импеданс и малый исходный).

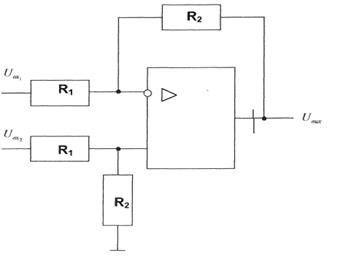
Рисунок 2.5. Дифференциальный усилитель

Схема дифференциального усилителя (рис. 2.5) пред-ставляет собой комбинацию инвертирующего и неинверти-рующего усилителей.

Для дифференциального усилителя можно записать

(2.34)

На практике часто необходимо ввести в исходный сигнал дифференциального усилителя постоянную составляющую. Это можно реализовать путем подключения источника смещения к инвертирующему входу операционного усилителя (рис.2.6).

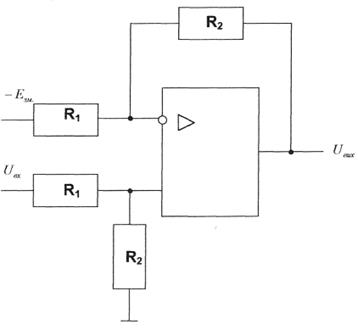
Рисунок 2.6. Смещение уровня

При введении смещения формула выходного напряжения имеет вид

(2.35)

Если входной сигнал изменяется в пределах от до и , то выходной сигнал будет изменяться от 0 до . Коэффициент усиления k определяется соотношением резисторов и .

Если выходной сигнал датчика - токовый, а для дальнейшей обработки сигнала требуется определённый уровень напряжения, то его необходимо превратить в напряжение и усилить до необходимого значения. Реализуем на базе операционного усилителя схему преобразователь ток-напряжение (рис. 2.7).

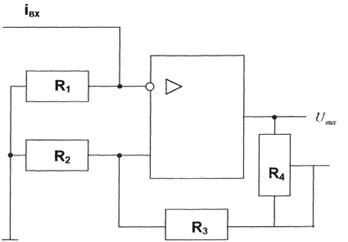
Рисунок 2.7. Преобразователь ток/напряжение

Преобразование входного тока в напряжение осуществляется на резисторе R₁, падение напряжения на котором усиливается на операционном усилителе, включенном по схеме неинвертирующего усилителя. Коэффициент усиления определяется соотношением резисторов R₃+R₄ и R₂. Резистор R₄ использован для коррекции значения коэффициента усиления.

В случаях, если необходимо ограничить диапазон изменения сигнала, например, напряжения, то можно воспользоваться амплитудными ограничителями (рис.2.8), представляющими собой инвертирующий усилитель, в цепь обратной связи которого включен стабилитрон.

Напряжение стабилизации и прямое напряжение стабилитрона определяют границы исходного напряжения. Исходное напряжение может быть инвертировано путем изменения полярности включения стабилитрона.

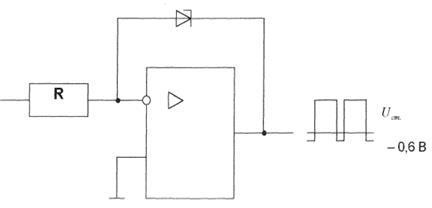
Рисунок 2.8. Амплитудный ограничитель

Для согласования датчиков с частотным выходом используют преобразователи частота-напряжение. В качестве такого преобразователя можно использовать микросхему К1108ПП1. Схема включения микросхемы в режиме преобразователя частота-напряжение приведена на рис 2.9.

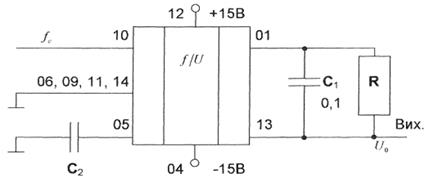
Рисунок 2.9. Преобразователь частота – напряжение

Для такого типа преобразователя можно записать

, (2.36)

где R- нагрузка усилителя и С₂ – входная ёмкость .

В дальнейшем аналоговые сигналы по параллельным каналам поступают на аналоговые коммутаторы (мультиплексоры). Для построения мультиплексоров рационально использовать многовыходные интегральные коммутаторы, например, серии 590. Условное графическое изображение мультиплексора на 8 входов приведено на рис. 2.10.

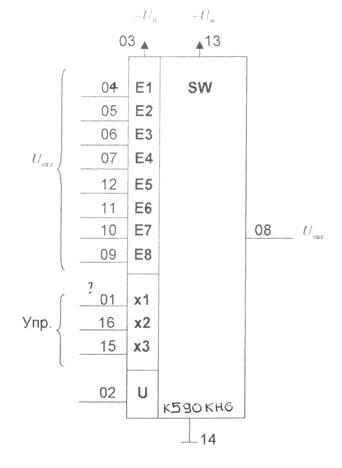
Рисунок 2.10. Мультиплексор 8 х 1

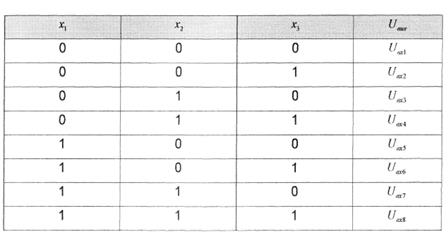
Данный мультиплексор имеет возможность коммутации сигналов, уровень которых достигает , в соответствии с табл. 2.2.

Таблица 2.2 – Коммутация сигналов мультиплексора

При необходимости построения мультиплексоров с большим числом каналов используют разные многоступенчатые конфигурации аналоговых коммутаторов (рис. 2.11).

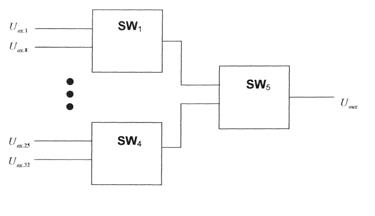
Рисунок 2.11. Мультиплексор 32 х 1

Применение мультиплексоров для переключения режимов работы и изменения параметров аналоговых корректирующих устройств позволяет получить простые и надежные схемы. Рассмотрим корректирующую схему пропорционально-интегрального регулятора (рис.2.12).

Эта схема реализует передаточную функцию

,

где - оператор Лапласа;

- коэффициент передачи пропорционального элемента (DA1);

- коэффициент передачи i-го потенциометра пропорционального элемента ( для R₁, для R₂);

- коэффициент передачи интегрального элемента (DA2);

- коэффициент передачи i-го потенциометра интегрирующего элемента ( для R₃, для R₄).

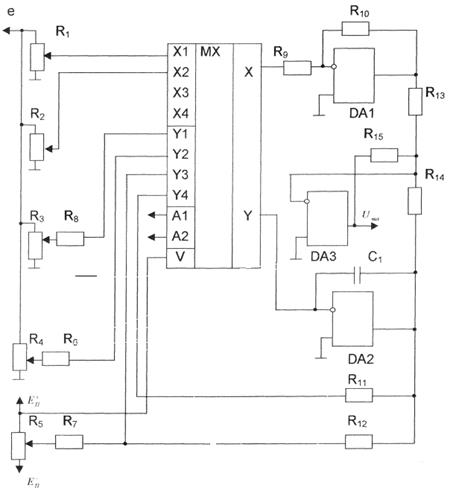
Рисунок 2.12. Корректирующая схема ПИ-регулятора

Приведенная схема позволяет управлять параметрами пропорционального и интегрирующего элементов. При сигнале «0» на входе DА2 схема работает в режиме формирования управляющего воздействия .

При сигнале «0» на входе DА1 параметры корректирующей схемы задаются потенциометрами R₁ и R₃, при сигнале «1» - R₂ и R₄. Необходимость изменения параметров корректирующей схемы возникает при управлении объектами или в случае, когда необходимо изменять параметры процесса управления.

Схема разрешает устанавливать нулевое значение исходного сигнала . Отключение исходного сигнала происходит при значениях, равных «0» и «1» на входах DА1 и DА2 соответственно. Для интегрирующего элемента в тот же момент устанавливается начальный нулевой заряд конденсатора С₁. Если на входах DА1 и DА2 формируется сигнал «1», то на выходе интегрирующего элемента устанавливается начальное значение напряжения, которое задается потенциометром R₅.

Для практической реализации схемы целесообразно выбирать параметры элементов равными соотношениям:

R₁₀/R₉=K_П; R₆=R₈; R₆C₁=1/K_j; R₇=R₁₂;
R₁₁С₁=; R₁₂C₂=; R₁₃=R₁₄=R₁₅,

где - постоянная времени разряда конденсатора С₁ при задании нулевого значения исходного сигнала ;

- постоянная времени перезаряда конденсатора С₁ при задании начального значения исходного сигнала .

Мультиплексоры также могут использоваться для моделирования дискретных элементов при переключениях , которые фиксируют значения непрерывных сигналов. В частности, можно реализовать модель квантователя непрерывного сигнала (рис.2.13а). Управляющие импульсы с частотой квантования поступают на вход счетного триггера DD1. На выходе триггера формируются импульсы с продолжительностью и периодом повторения (рис.2.13б).

Импульсы вызывают переключение мультиплексора DA1 таким образом, что на протяжении одного периода входной сигнал поступает через резистор R₁ на конденсатор С₁, а вход операционного усилителя DA2 подключается к конденсатору С₂. На протяжении второго полупериода через резистор R₁ заряжается конденсатор С₂, а на вход операционного усилителя подается сигнал, зафиксированный на конденсаторе С₁. Таким образом, при работе схемы на вход операционного усилителя подается кусочно-постоянный сигнал, значение которого равняется значению входного сигнала в момент переключения триггера DD1. Операционный усилитель необходимый для уменьшения тока разряда конденсаторов С₁ и С₂ через сопротивление нагрузки. При R₂=R₃ модель квантователя имеет единичный коэффициент передачи. Емкости конденсаторов С₁ и С₂ одинаковые, их выбирают таким образом, чтобы разряд через входные звенья операционного усилителя на протяжении одного периода не превышал заданной погрешности фиксирования сигнала при выполнении условия

,

где r_m - внутреннее проходное сопротивление открытого электронного ключа мультиплексора.

Если постоянная времени заряда конденсатора намного меньше , то к моменту окончания каждого периода квантования он оказывается заряженным до напряжения входного сигнала .

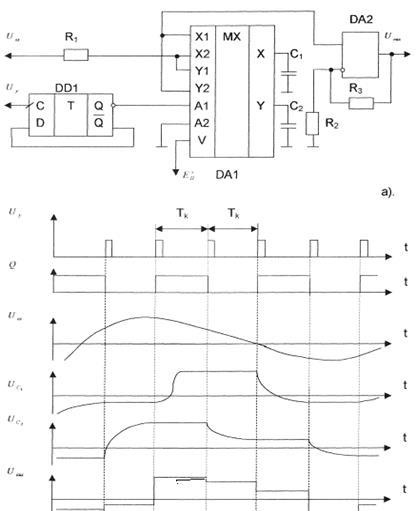
Рис 2.14. Схема модели квантователя непрерывного сигнала (а) и эпюры напряжения

Рисунок 2.13 – Схема модели квантователя непрерывного сигнала (а) и эпюры напряжений (б)

Для запоминания переменных аналоговых сигналов на время преобразования, коммутации и других операций в системах используют схемы выборки-хранения (рис. 2.14).

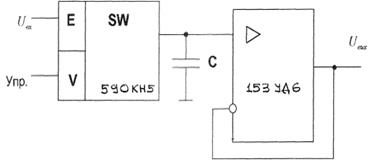
Рисунок 2.14. Схема выборки-хранения

Элементом памяти схемы выборки-хранения является конденсатор С, который подключается на время выборки к источнику сигнала. Время выборки сигнала определяется из соотношения

, (2.37)

где - сопротивление открытого ключа (для К590КН5); - сопротивление источника сигнала; С - емкость конденсатора.

В практических схемах широко используется микросхема К1100СК2, предназначенная для выборки и хранения аналогового сигнала, который запоминается по команде, поступающей на логический вход С₁, входной сигнал подаётся на , а постоянное значение сигнала поддерживается на выходе . Схема включения К1102СК2 приведена на рис.2.15.

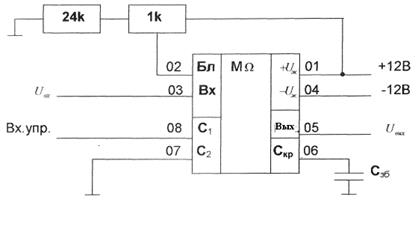
Рисунок 2.15. Схема выборки/хранения

Входной сигнал равен = 5В. Режиму выборки соответствует «1» на входе управления C_1, а режиму хранения- «0» при C_зб = 1000пФ и .

После необходимых преобразований сигналов, которые поступают от датчиков, нужно перейти к процедуре преобразования аналоговых сигналов в цифровой код и дальнейшей их обработки.

2.4. Аналого-цифровые и цифро-аналоговые преобразователи

Неотъемлемой частью современных автоматических систем контроля и управления являются преобразователи аналоговых и цифровых сигналов:

• аналого-цифровые преобразователи (АЦП);
• цифро-аналоговые преобразователи (ЦАП).

ЦАП - устройство, которое создает на выходе аналоговый сигнал (ток и напряжение), пропорциональный входному сигналу. При этом значение выходного сигнала зависит от опорного напряжения, которое определяет полную шкалу выходного сигнала. Если вместо опорного напряжения использовать любой аналоговый сигнал, то выходной сигнал ЦАП будет пропорциональный произведению входных цифровых и аналоговых сигналов. В АЦП цифровой код на выходе определяется отношением преобразующего входного аналогового сигнала к опорному сигналу, который отвечает полной шкале. Если опорный сигнал изменяется по любому закону, то цифровой сигнал на выходе АЦП будет пропорциональный отношению двух аналоговых (входного и опорного) сигналов. В этом случае АЦП можно рассматривать как измеритель отношений или делитель напряжения с цифровым выходом.

В зависимости от области применения на входе ЦАП или выходе АЦП могут быть или однополярные цифровые коды, или биполярные. К первым относятся прямой двоичный и двоично-десятичный коды, а ко вторым - двоичный код со смещением.

В стандартном двоичном коде старший разряд имеет вес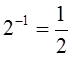

от значения полной шкалы. Разряд, который следует за старшим разрядом, имеет вес и так далее в направлении к младшему разряду с весом , где М - число разрядов преобразователя.

Сумма всех разрядов определяет значение полной шкалы преобразователя. Двоичный код со смещением отличается от прямого тем, что ноль двоичного числа и ноль аналоговой величины не совпадают, как в стандартном двоичном коде, а смещены таким образом, что в старшем разряде устанавливается «0» для всех отрицательных и «1» для всех положительных величин. Поэтому старший разряд определяет полярность цифрового кода (рис. 2.16). Из рисунка видно, что прямой код дает возможность использовать в два раза большую раздельность по сравнению со смещенным.

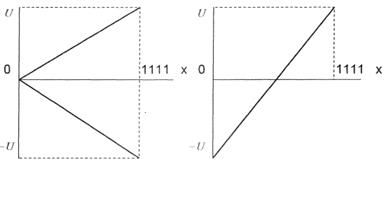
Рисунок 2.16. Графики соответствия цифровых кодов и аналоговых напряжений

Основными параметрами, которые характеризуют ЦАП и АЦП, являются:

статические характеристики – это нелинейность, монотонность, коэффициент преобразования, абсолютная и относительная погрешность, смещение нуля, раздельная способность;

динамические характеристики – это время установ-ления, время преобразования.

Раздельная способность определяет число дискретных значений исходного сигнала преобразователя, которые составляют его границы преобразования. Может выражаться или в процентах, или в долях к полной шкале, например, двенадцатиразрядный АЦП имеет раздельную способность 1/4096 или 0,0245% полной шкалы.

Нелинейность характеризуется отклонением значений реальной характеристики преобразователя от прямой. Преобразователь считается линейным, если его максимальная погрешность линейности не превышает половины младшего разряда преобразователя.

Монотонность преобразователя означает, что при каждом приращении входного сигнала происходит прирост выходного сигнала - первая производная от непрерывной функции выход-вход должна быть меньшей нуля.

Коэффициент преобразования - это отношение прироста выходного сигнала к приросту входного сигнала, определяющий угол отклонения характеристики. Для идеального ЦАП отклонение характеристики должно быть таким, чтобы при включении всех разрядов исходное напряжение преобразователя было меньше опорного напряжения на величину младшего разряда.

Степень отклонения реального значения коэффициента преобразования от расчетного характеризуется абсолютной погрешностью, под которой понимают разность между номинальным значением напряжения полной шкалы преобразователя и фактическим его значением.

Погрешность нуля (смещение) для ЦАП - это исходное напряжение ЦАП с нулевым входным кодом, а для АЦП - среднее значение входного напряжения АЦП, которое необходимо для получения нулевого кода на его выходе.

Время установления исходного сигнала ЦАП является важным динамическим параметром и определяется как интервал времени, на протяжении которого исходный аналоговый сигнал ЦАП при изменении кодовой комбинации на его цифровых входах достигает своего установленного значения, которое не превышает предельной погрешности.

Рассмотрим характеристики, которые помогают выбрать тип преобразователя для конкретного применения в разрабатываемых системах и устройствах. Практическую реализацию многоразрядных схем АЦП и ЦАП рационально проводить на основе микросхем, которые содержат основные блоки преобразователей в одном корпусе.

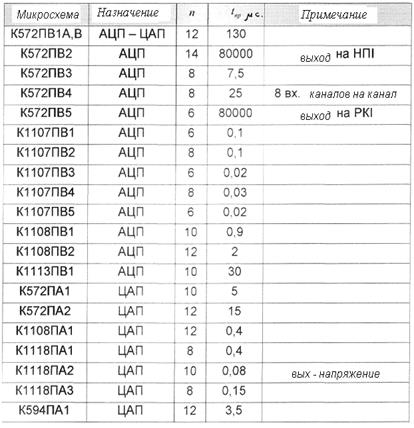
В табл. 2.3 приведены основные типы и параметры микросхем, на основе которых реализуются аналого-цифровые и цифро-аналоговые преобразователи (n -число разрядов, t_np - время преобразования).

Рассмотрим схемы включения и функциональные возможности микросхемы К572ПВ1, которую можно использовать как в режиме АЦП, так и в режиме ЦАП.

На рис. 2.17 приведена схема включения микросхемы в режим АЦП.

Этот АЦП имеет входные каскады с тремя состояниями, благодаря чему может выдавать информацию на системную шину микропроцессорного контроллера. Кодовые выходы могут использоваться не только для вывода, а также для введения дискретных сигналов, так как кодовый канал двунаправленный. Переключение кодового канала на ввод или вывод выполняется сигналом, который подается на вход V (режим).

Таблица 2.3 – Типы АЦП - ЦАП

Если V = 0 - вывод, то V = 1 - ввод. Перевод канала в высокоимпедансное состояние выполняется при LE=0 (управление 8 младшими разрядами канала) и НЕ=0 (управление 4 старшими разрядами).

Благодаря наличию этих входов информация с АЦП может выводиться побайтно на восьмиразрядную шину данных.

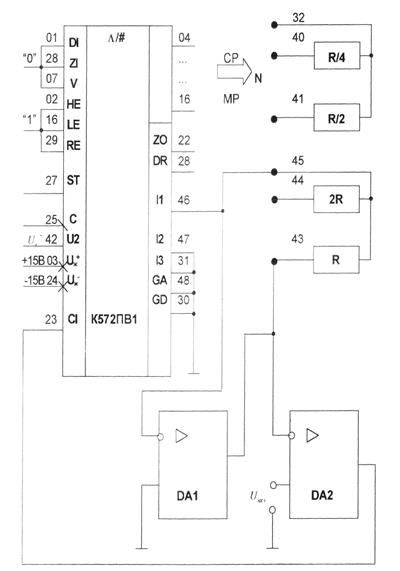
Рисунок 2.17. Режим АЦП

Работа преобразователя синхронизируется тактовыми импульсами, которые подаются на вход С с частотой не больше 250 кГц. Опорное напряжение должно иметь противоположную полярность напряжения . Операционный усилитель DA1 используется для преобразования в напряжение выходного тока. В качестве резистора обратной связи DA1 используется один из резисторов, которые входят в микросхему (выводы 43 и 45) . Компаратор DA2 сравнивает исходное напряжение DA1 с . Результат сравнения подается на вход С1. Запуск АЦП проводится положительным импульсом, который подается на вход ST (старт). Цикл преобразования содержит 28 периодов тактовых импульсов, после чего на выходе DR (готовность данных) формируется положительный импульс. Для организации циклической работы АЦП необходимо соединить между собой ZO (выход цикла) и ZI (вход цикла).

Схема включения микросхемы К572ПВ1 в режиме ЦАП приведена на рис. 2.18.

В этом случае на вход V подается «1» и через кодовый канал входной код N записывается в регистр АЦП. Внешняя кодовая комбинация в регистр может быть записана также последовательно по входу DI синхронно с парами тактовых импульсов, начиная от младших разрядов. Вход RE разрешает изменение кода во входном регистре при RE=1.

Если RE=0 – формируется сигнал сохранения введен-ного кода. Выводы GA и GD - аналоговая и цифровая земля.

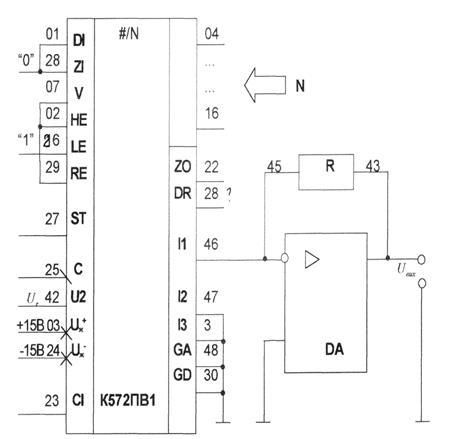
Рисунок 2.18. Режим ЦАП

Список литературы

Романенко В.Д., Игнатенко Б.В. Адаптивное управление технологическими процессами на базе микро-ЭВМ. - К.: Высшая школа, 1990.

Микропроцессоры /Под ред. Л.Н. Преснухина - М.: Высшая школа, 1986.- Т.2.

Гутников B.C. Интегральная электроника в измерительных устройствах. - Л.: Энергоатомиздат, 1988.

Цифровые и аналоговые микросхемы: Справочник /Под ред. С.В. Якубовского - М.: Радио и связь, 1990.

Микроэлектронные устройства автоматики /Под ред. А.А.Сазонова - М.: Энергоиздат, 1991.