Согласно теореме В. А. Котельникова, непрерывное колебание u(t) может быть передано по линии связи с необходимой точностью путем передачи отдельных мгновенных значений этого колебания

(9.50)

взятых для моментов времени, отстоящих друг от друга на величину , где F — наивысшая частота, содержащаяся в колебании u(t).

В системах связи, основанных на этом принципе (импульсные системы), для передачи колебания u(t) используется периодическая последовательность импульсов

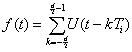(9.51)

При этом один из параметров этой последовательности изменяется в соответствии с изменением мгновенных значений (9.50) передаваемого колебания u(t).

Модулированную последовательность импульсов на выходе первой ступени модуляции можно записать в виде

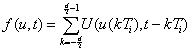(9.52)

В выражениях (9.51) и (9.52) пределы суммы взяты на основании предположения о том, что сообщение передается в интервале времени от - до , где T — достаточно большая величина по сравнению с периодом повторения импульсов , где р — тактовая частота. Полагаем, что d — целое число; U(t) — уравнение огибающей импульса, причем U(t)=0 при t<0 и t>, где — длительность импульса.

Для передачи колебания f(u, t) по радио необходимо применить еще одну ступень модуляции. При этом может быть использована любая из систем модуляции, рассмотренных в § 9.2.

Сигнал, излучаемый передатчиком, представляет собой колебания, зависящие от времени и передаваемого сообщения:

(9.53)

Потенциальную помехоустойчивость импульсных систем модуляции можно определить, исходя из общей ф-лы (9.12) или соответственно из ф-лы (9.19) для прямых систем модуляции несущей и ф-лы (9.21) —для интегральных систем.

Обозначение систем в дальнейшем изложении принято в виде короткой записи ХУZ—АВ, где первые три буквы обозначают вид импульсной модуляции в каналах, а символ АВ — способ модуляции несущей.

Подробные исследования помехоустойчивости импульсных систем модуляции читатель может найти в работе [2]. Здесь мы ограничимся лишь анализом полученных там результатов. Потенциальная помехоустойчивость систем АИМ-АМ, АИМ-БМ и АИМ-ОМ оказывается равной потенциальной помехоустойчивости соответствующих аналоговых систем AM, БМ, ОМ. Для этих систем помехоустойчивость не зависит от формы и длительности импульсов и ширины спектра сигнала.

В системах АИМ-ФМ и АИМ-ЧМ помехоустойчивость может быть повышена за счет расширения полосы частот, занимаемой сигналом.

Обобщенный выигрыш в системе ФИМ-АМ определяется следующим выражением:

(9.54)

где — коэффициент, зависящий от формы импульса, — максимальная девиация импульса. Как видим, помехоустойчивость системы ФИМ зависит от формы импульса. При оптимальном выборе параметров системы ФИМ-АМ: ,p = 2Fm, ,

(9.55)

При — , что соответствует треугольной форме импульсов,

(9.56)

Это совпадает с ф-лой (9.30) для системы с частотной модуляцией. Следовательно, потенциальная помехоустойчивость системы ФИМ-АМ при оптимальном выборе параметров и системы ЧМ одинакова.

Система с частотно-импульсной модуляцией (ЧИМ) имеет ту же потенциальную помехоустойчивость, что и система ФИМ-АМ.

Применение ЧМ и ФМ с ФИМ позволяет обеспечить более высокую помехоустойчивость по сравнению с системой ФИМ-АМ лишь при достаточно больших индексах модуляции. При использовании же коротких импульсов применение высоких индексов модуляции может оказаться практически неосуществимым или нецелесообразным.

Важным достоинством системы ФИМ-АМ является то, что ее передающее устройство в этой системе работает в режиме передачи кратковременных импульсов. В системах ФИМ-ЧМ и ФИМ-ФМ это преимущество теряется.

Формулы, определяющие потенциальную помехоустойчивость систем с ФИМ, справедливы и для соответствующих систем с ШИМ при u(t)=0. Однако при этом следует помнить, что в системе с ШИМ средняя длительность импульса больше, чем в системе с ФИМ. Вследствие этого при одинаковой амплитуде импульса в системе ШИМ-АМ затрачивается большая средняя мощность передатчика, чем в системе ФИМ-АМ.

Существенным преимуществом импульсных методов модуляции является возможность эффективного амплитудного ограничения по максимуму и минимуму. Это позволяет значительно повысить помехоустойчивость приема при малом уровне помех. Сказанное не относится к системе АИМ, в которой ограничение импульсов по амплитуде недопустимо.

В настоящее время широко применяется пороговый прием, при котором модулируемые параметры импульса определяются в момент перехода его через некоторый уровень (порог). При большом уровне помех отдельные выбросы помехи могут превысить уровень порога я вызвать ложные срабатывания выходных устройств в промежутках между импульсами. Кроме того, выбросы помехи могут подавлять отдельные импульсы сигнала. Если пиковое значение помехи равно или больше порога срабатывания приемника, то вероятность ложных срабатываний резко увеличивается и прием становится практически невозможным.

Таким образом, в импульсных системах с амплитудной модуляцией несущей, а также в системах передачи ОМ и БМ порог помехоустойчивости определяется порогом срабатывания приемника. Обычно пороговый уровень в приемнике выбирается равным половине амплитуды сигнала. В этом случае порог помехоустойчивости при пикфакторе помехи

(9.57)

где п — число каналов.

Пороговая мощность при этом равна:

(9.58)

При оптимальном выборе параметров системы Fτ0 = 1 и

(9.59)

Полученные выражения показывают, что пороговая мощность сигнала в импульсных системах с амплитудной модуляцией несущей <не зависит от полосы пропускания приемника. Это обусловливает одно из важнейших преимуществ импульсных систем по сравнению, например, с частотной модуляцией. Действительно, выбирая достаточно малую длительность импульса, можно увеличить выигрыш системы -у. не увеличивая при этом пороговую мощность сигнала. В системе же с частотной модуляцией увеличение выигрыша γ за счет расширения полосы частот канала ведет к увеличению пороговой мощности сигнала.

В импульсных системах с частотной модуляцией несущей порог помехоустойчивости определяется системой модуляции несущей.