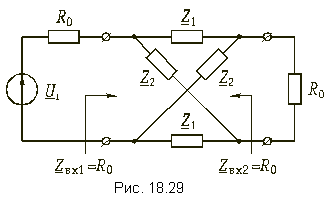
Пассивные корректоры. Фазовые корректоры должны иметь постоянное входное сопротивление и постоянное ослабление, которые не зависят от частоты. Таким условиям удовлетворяют симметричные мостовые четырехполюсники (рис. 18.29), у которых сопротивления Z1 и Z2 реактивные и взаимообратные, т. е.:
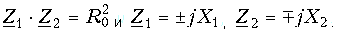
Такие четырехполюсники имеют с обеих сторон одинаковые характеристические сопротивления:
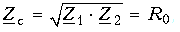
поэтому их легко согласовывать с внутренним сопротивлением генератора и сопротивлением нагрузки.
Рабочее ослабление мостового симметричного согласованно включенного четырехполюсника с взаимно-обратными сопротивлениями Z1 и Z2 равно нулю на всех частотах: A(w) = 0, т. е. эта схема не вносит никакого дополнительного ослабления сигнала.
Операторная передаточная функция по напряжению схемы рис. 18.29 имеет вид:
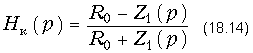
Комплексная передаточная функция по напряжению схемы рис. 18.29, в которой Z1 и Z2 - реактивные двухполюсники, может быть вычислена по формуле:
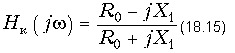
Нетрудно видеть, что модуль передаточной функции (18.15) равен 1, а аргумент и ГВП вычисляются по формулам:
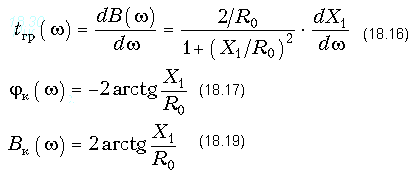
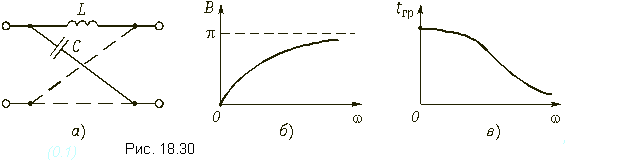
Формулы (18.16), (18.17) и (18.18) показывают, что фазо-частотная характеристика, фазовая постоянная и характеристика группового времени запаздывания корректора зависят только от вида двухполюсника X1. На практике используются типовые звенья пассивных фазовых корректоров первого и второго порядков.
На рис. 18.30, а изображена схема фазового корректора 1-го порядка, в котором двухполюсником Z1 является индуктивность Z1(p) = pL, а двухполюсником Z2 - емкость Z2(p) = 1/(pC). Операторная передаточная функция этого корректора в соответствии с (18.14) имеет вид:
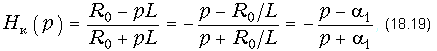
где a1 = R0/L.
Рабочая фазовая постоянная B(w) и ГВП в соответствии с формулами (18.17) и (18.18)
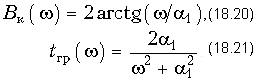
Графическое изображение данных характеристик показано на рис. 18.30, б и в. На рис. 18.31, а изображена схема фазового корректора 2-го порядка, с двухполюсником Z1, состоящим из последовательного соединения элементов L1 и C1, т. е. Z1(p) = pL1 + 1/(pC1). Операторная передаточная функция такого корректора в соответствии с (18.14) имеет вид:
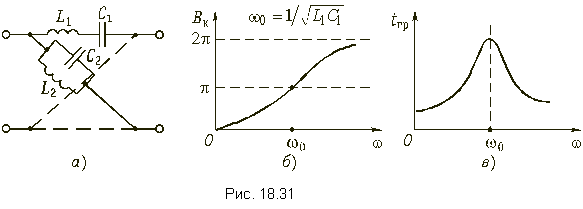
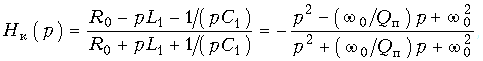
где w02 = 1/(L1C1), Qп = 1/(w0R0C1) -добротность полюса передаточной функции. Комплексная передаточная функция корректора получается при p = jw:
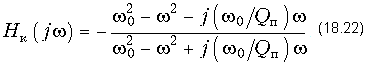
Модуль функции равен 1, а рабочая фазовая постоянная B(w) и ГВП tгр(w) вычисляются в соответствии с (18.17) и (18.18) по формулам:
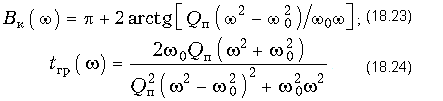
Графики зависимостей B(w) и tгр(w) фазового корректора 2-го порядка приведены на рис. 18.31, б и в. Если известны коэффициенты передаточной функции w0, Qп и нагрузка R0, то параметры элементов корректора рассчитываются по формулам
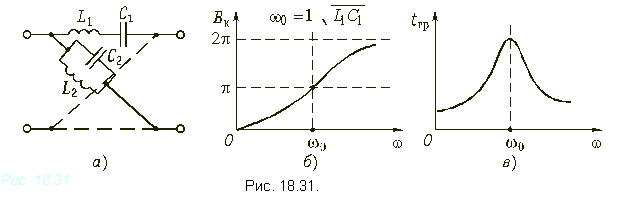
Пример. Фазовый корректор (рис. 18.30, а) имеет элементы L1 = 100 мГн, R0 = 500 Ом. Рассчитать и построить графики частотных зависимостей фазовой постоянной Bк(f) и группового времени прохождения tгр(f) в диапазоне частот от 0 до 10 кГц.
Фазовая характеристика B(w) рассчитывается по формуле (18.20), поэтому:
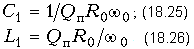
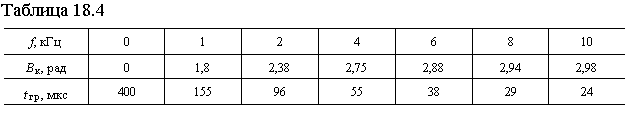
ГВП tгр(w) рассчитывается по формуле (18.21), поэтому:
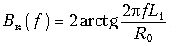
Подставляя в выражения для Bк(f) и tгр(f) значения L1 = 10Ч10-3 Гн и R0 = 500 Ом, получаем:
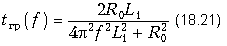
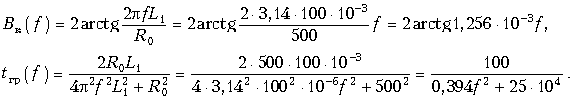
Результаты расчета Bк(f) и tгр(f) в диапазоне частот f = 0 ё 10 кГц приведены в таблице 18.4, а графики - на рис. 18.32, а и б.
Пример. Схема фазового корректора приведена на рис. 18.31, а. Рассчитать и построить графики частотных зависимостей фазовой постоянной Bк(f) и ГВП tгр(f) в диапазоне частот от 0 до 10 кГц для двух случаев: 1) R0 = 600 Ом; L1 = 36 мГн, С1 = 0,025 мкФ; 2) R0 = 600 Ом; L1 = 36 мГн, С1 = 0,05 мкФ.
Фазовая характеристика Bк(w) корректора рассчитывается по формуле (18.23), а ГВП tгр(w) по формуле (18.24), поэтому:
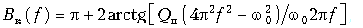
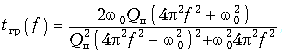
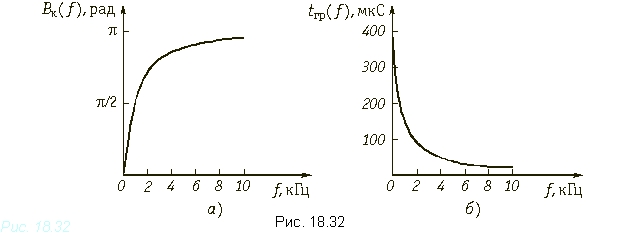
где w02 = 1/(L1C1), Qп = 1/(w0R0C1).
Рассчитаем значения w02 и Qп для двух случаев задания параметров элементов корректора:
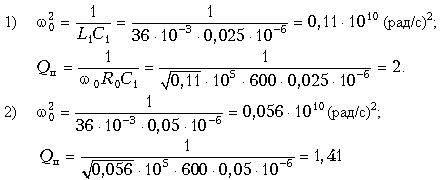
Подставляя значения w02 и Qп в выражения для расчета Bк(f) и tгр(f), рассчитываем эти характеристики в диапазоне частот от 0 до 10 кГц и заносим результаты расчета в таблицу 18.5 для случая 1) и в таблицу 18.6 для случая 2). Поскольку график tгр(w) имеет максимум (рис. 18.31, в), то для определения частоты этого максимума берем производную dtгр(w) и, приравняв ее к нулю, находим:
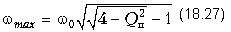
для первого случая (Qп = 2) и fmax = 2,42 кГц для второго случая (Qп =1,41).
В общем случае анализ выражения (18.27) показывает, что при Qп Х ГВП имеет максимум на частоте f = 0, а при Qп < = 1,73 максимум ГВП - на частоте fmax.
Значение tгрmax рассчитывается по формуле:
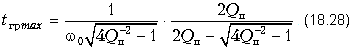
Для второго случая, когда Q = 1,41, имеем tгрmax = 144 мкС. Следует также отметить, что при Qп . 1 формулы (18.27) и (18.28) существенно упрощаются:
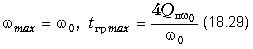
Графики зависимостей Bк(w) и tгр(w) для двух случаев приведены на рис. 18.33 (обозначены цифрами 1 и 2).
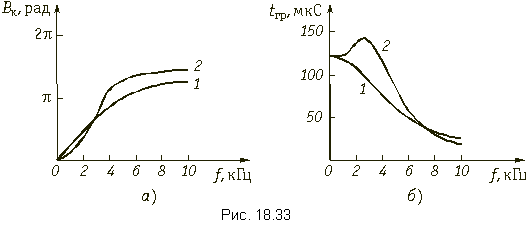
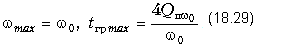
Мостовая схема не всегда удобна в реализации, так как является уравновешенной. Существует ряд эквивалентных схем в виде неуравновешенной схемы, как показано на рис. 18.34. Заметим, что на практике добротность полюса больше единицы и поэтому чаще используется схема рис. 18.34, а, что удобно, так как она не содержит связанных индуктивностей с заданным коэффициентом связи. Неуравновешенные схемы по сравнению с мостовыми содержат вдвое меньше элементов.
Активные корректоры. Помимо пассивных фазовых корректоров применяют активные фазовые корректоры. Кроме пассивных RC или RLC-элементов схемы активных корректоров содержат операционные усилители. Существуют активные фазовые звенья 1-го и 2-го порядков. На рис. 18.35 приведена схема фильтрового звена на операционном усилителе. Передаточная функция этого звена вычисляется по формуле:
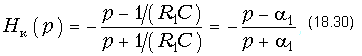
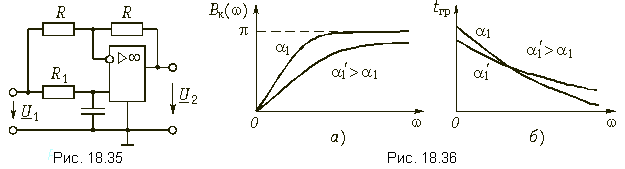
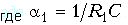
Выражение (18.30) аналогично формуле для расчета передаточной функции пассивного фазового корректора (18.19), т. е. схема, приведенная на рис. 18.35, - это активный корректор 1-го порядка. Фазовые характеристики B(w) и ГВП данного звена, также как у пассивного корректора 1-го порядка, вычисляются по формулам
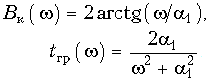
График Bк(w) монотонно нарастает от Bк(0) = 0 до Bк(Ґ) = p, а график tгр(w) монотонно убывает от tгр(0) = 2/a1 до tгр(Ґ) = 0. На рис. 18.36 показаны графики Bк(w) и tгр(w), построенные для разных значений a1 активного корректора 1-го порядка.
На рис. 18.37 приведена еще одна схема активного фазового корректора, также построенная на основе активного фильтрового звена. Если в схеме рис. 18.37 задать R3 = nR2, R4 = nR2/(n -1), n > 1, то передаточная функция, рассчитанная, например, с помощью метода узловых напряжений, будет иметь вид:
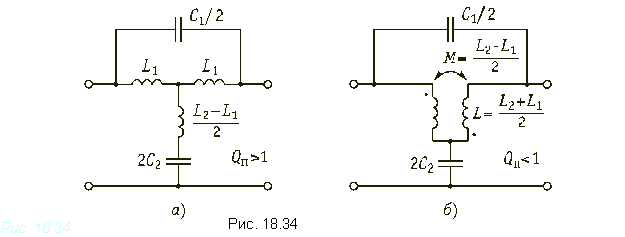

Это передаточная функция фазового корректора (сравни с формулой (18.14)).
Если в качестве двухполюсника Z выбрать емкость, то передаточная функция (18.31) принимает вид (18.30):
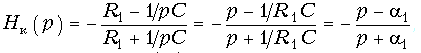
т. е. схема на рис. 18.37 - это схема фазового корректора 1-го порядка. Когда в качестве двухполюсника Z используется последовательный LC-контур, то получается передаточная функция фазового корректора 2-го порядка:
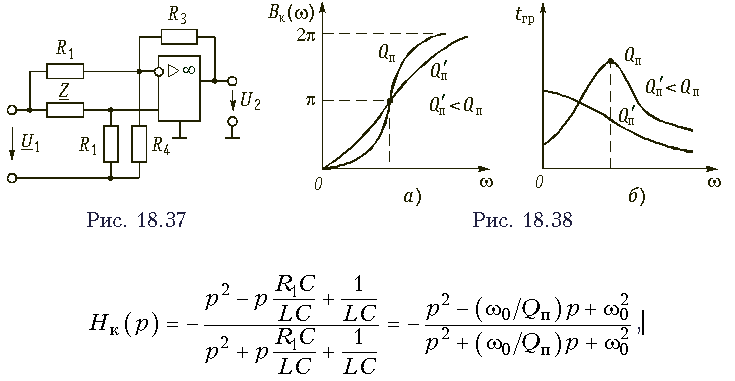 , где w02 = 1/(LC), Qп = 1/(w0R1C) - добротность полюса передаточной функции.
, где w02 = 1/(LC), Qп = 1/(w0R1C) - добротность полюса передаточной функции.
Графики частотных зависимостей Bк(w) и tгр(w) данного корректора, полученные для разных значений Qп, приведены на рис. 18.38. Хотя активные ARZ-фазовые корректоры имеют индуктивность, но преимуществом их по сравнению с пассивными корректорами является меньшее количество элементов при том же порядке передаточных функций.
Пример. Определить передаточную функцию фазового корректора, построенного по схеме рис. 18.35, в которой в качестве двухполюсника Z используется параллельный LC-контур. Рассчитать и построить качественно частотную характеристику ГВП tгр(f) корректора в диапазоне частот от 0 до 5 кГц для элементов цепи R1 = 37,5 Ом, L = 36 мГн, C = 1,6 мкФ.
Найдем сопротивление Z(p) параллельного LC-контура:
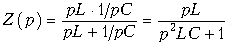
Подставив Z(p) в формулу (18.31), получим передаточную функцию фазового корректора:
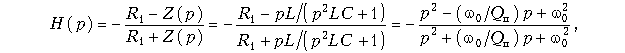
где w02 = 1/(LC), Qп = w0R1C.
ГВП рассчитывается по формуле (18.24), в которой w = 2pf,
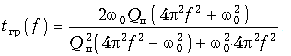
Находим значения w02 и Qп:
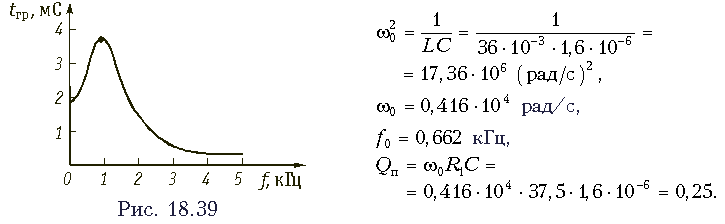
Поскольку , то находим значения wmax и tгрmax по формулам (18.27) и (18.28):
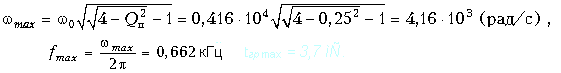
Рассчитываем значения tгр(f) на частотах f1 = 0 и f2 = 5 кГц по формуле (18.24). Получаем tгр(f1) = 1,92 мС и tгр(f2) = 0,12 мС. График зависимости tгр(f) приведен на рис. 18.39.
Синтез фазовых корректоров. При синтезе фазовых корректоров задаются характеристика ГВП корректируемой цепи, сопротивление нагрузки R0, точность коррекции и диапазон частот wн ... wв, в котором осуществляется коррекция. Вначале определяют требуемую характеристику фазового корректора. Для этого задают постоянное значение ГВП t0, которое должно быть несколько больше максимального значения ГВП цепи (рис. 18.12, б):
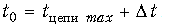
Затем любым способом определяют площадь Sк под характеристикой требуемого ГВП корректора, например, площадь можно рассчитать по формуле:
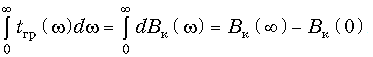
После этого приближенно можно определить число фазовых звеньев второго порядка, необходимых для коррекции, так как площадь под кривой группового времени фазового звена второго порядка равна 2p:
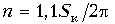
В данной формуле коэффициентом 1.1 учитывается то, что не вся площадь под характеристикой фазового звена попадает в диапазон коррекции.
Зная число звеньев, задаемся в первом приближении их параметрами w0k и Qпk, k = 1 ... n. Для начала частоты распределяются равномерно, добротность определяют из условия требуемой величины группового времени звена на частоте wmaxk. Эта величина выбирается на 10 ... 20% меньше, чем требуемое групповое время корректора на этой частоте. Из сказанного и формулы (18.27) следует:
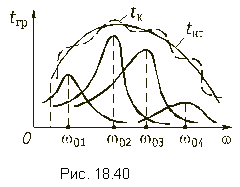
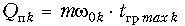
где m = 0,8 ... 0,9. На рис. 18.40 показаны характеристики ГВП четырех фазовых звеньев, требуемая и реальная характеристики ГВП корректора. Далее с применением компьютерных программ решается оптимизационная задача в общей постановке:
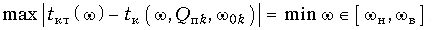
Если полученный минимум меньше или равен требуемой точности коррекции, то по заданным Qпk, w0k и R0 рассчитывают элементы L1k и C1k мостовой схемы фазового звена (рис. 18.31, а). Остальные элементы находят из условия, что двухполюсники Za и Zb обратные:
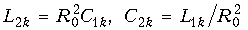
Если полученная точность коррекции не удовлетворяет требованиям, то увеличивают число звеньев и повторяют расчет также с помощью компьютера. С синтезом активных фазовых корректоров можно познакомиться в специальной литературе.

