14.4.1. Пример генерирования ключа с использованием линейного регистра сдвига с обратной связью

14.4.2. Слабые места линейных регистров сдвига с обратной связью

14.4.3. Синхронные и самосинхронизирующиеся системы поточного шифрования

Ранее мы определили разовое заполнение как систему шифрования со случайным одноразовым ключом, который обеспечивает безусловную защищенность. Реализовать разовое поточное заполнение можно с использованием действительно случайного потока ключей (ключевая последовательность никогда не повторяется). Таким образом, совершенная секретность может достигаться для бесконечного числа сообщений, так как каждое сообщение шифруется с помощью разных частей случайного ключевого потока. Развитие схем поточного шифрования — это попытка имитации схем одномоментного заполнения. Большой упор делается на генерации ключевых потоков, которые должны выглядеть случайными. Реализовать такие последовательности можно с помощью соответствующих алгоритмов. Названная технология поточного шифрования использует псевдослучайные последовательности; их название отражает тот факт, что они выглядят случайными для случайного наблюдателя. Статистические свойства двоичных псевдослучайных последовательностей подобны получаемым при случайном подбрасывании симметричной монеты. В то же время, разумеется, эти последовательности являются детерминистическими (см. раздел 12.2). Данные технологии популярны, поскольку алгоритмы шифрования и дешифрования воплощаются с использованием регистров сдвига с обратной связью. На первый взгляд может показаться, что поточный псевдослучайный ключ может обеспечивать ту же защищенность, что и метод одномоментного заполнения, поскольку период последовательности, порожденной линейным регистром сдвига, составляет 2^n-1 бит, где п — количество разрядов в регистре. Если псевдослучайная последовательность воплощается с помощью 50-разрядного регистра и дискретности в 1 МГц, последовательность будет повторяться каждые 2⁵⁰-1 микросекунды, или каждые 35 лет. В эпоху больших интегральных схем совсем несложно реализовать схему с 100 разрядами. В этом случае последовательность будет повторяться каждые 410¹⁶ лет. Следовательно, можно предположить, что поскольку псевдослучайная последовательность не повторяется в течение такого длительного периода, она может казаться действительно случайной и давать совершенную секретность. Но все же существует одно важное отличие псевдослучайной последовательности от действительно случайной последовательности, используемой в методе одномоментного заполнения. Псевдослучайная последовательность генерируется алгоритмом. Таким образом, если известен алгоритм, то известна и сама последовательность.

14.4.1. Пример генерирования ключа с использованием линейного регистра сдвига с обратной связью

В технологии поточного шифрования для генерации псевдослучайной ключевой последовательности обычно используются регистры сдвига. Регистр сдвига может быть превращен в генератор псевдослучайной последовательности путем введения контура обратной связи, который вычисляет новый элемент для первого разряда, основываясь на предыдущих п элементах. Говорят, что регистр является линейным, если линейна операция, производимая в контуре обратной связи. В разделе 12.2 мы уже рассматривали пример генератора псевдослучайной последовательности. На рис. 14.13 этот генератор приведен повторно. В данном случае разряды регистра удобно нумеровать так, как показано на рис. 14.13, где n =4, а выходы разрядов 1 и 2 суммируются по модулю 2 (линейная операция) и передаются обратно на разряд 4. Если начальное состояние разрядов (x4, x3, x2, x1,) — это 1000, то следующие состояния будут выглядеть как 1000, 0100, 1001, 1100 и т.д. Выходная последовательность составлена из битов, снимаемых с крайнего правого разряда регистра, т.е. 111101011001000, где крайний правый бит в последовательности является самым ранним, а крайний левый — наиболее поздним. При данном произвольном n-разрядном линейном регистре сдвига с обратной связью выходная последовательность в конечном счете периодична.

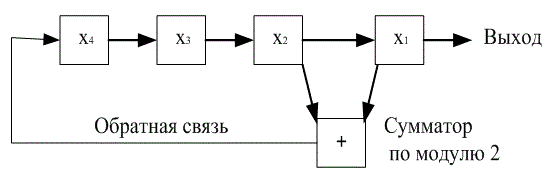
Рис. 14.13. Пример линейного регистра сдвига с обратной связью

14.4.2. Слабые места линейных регистров сдвига с обратной связью

Схема шифрования, в которой для порождения ключевого потока применяются линейные регистры сдвига с обратной связью (linear feedback shift register — LFSR), является очень уязвимой по отношению к атакам. Чтобы определить отводы обратной связи, начальное состояние регистра и всю последовательность кода, криптоаналитику требуется всего 2п бит открытого текста и соответствующий им шифрованный текст. Как правило, 2n намного меньше периода 2ⁿ-1. Проиллюстрируем эту уязвимость с помощью примера регистра, изображенного на рис. 14.13. Пусть криптоаналитику, который ничего не знает о внутренних связях регистра, удалось получить 2п = 8 бит шифрованного текста и их открытый эквивалент.

Открытый текст: 01010101

Шифрованный текст: 00001100

Здесь крайний правый бит получен первым, а крайний левый — последним.

Чтобы получить фрагмент ключевого потока 01011001 (рис. 14.14), криптоаналитик складывает обе последовательности по модулю 2. Ключевой поток показывает содержание регистров в различные моменты времени. Крайние правые четыре ключевых бита показывают содержание регистра сдвига в момент t1. Если последовательно «сдвигать» эту четверку на один символ влево, то получим содержимое регистра в моменты t2, t3, t4. Используя линейную структуру регистра сдвига, можно записать следующее.

g4x4 + g3x3 + g2x2 + gixi= x5 (14.27)

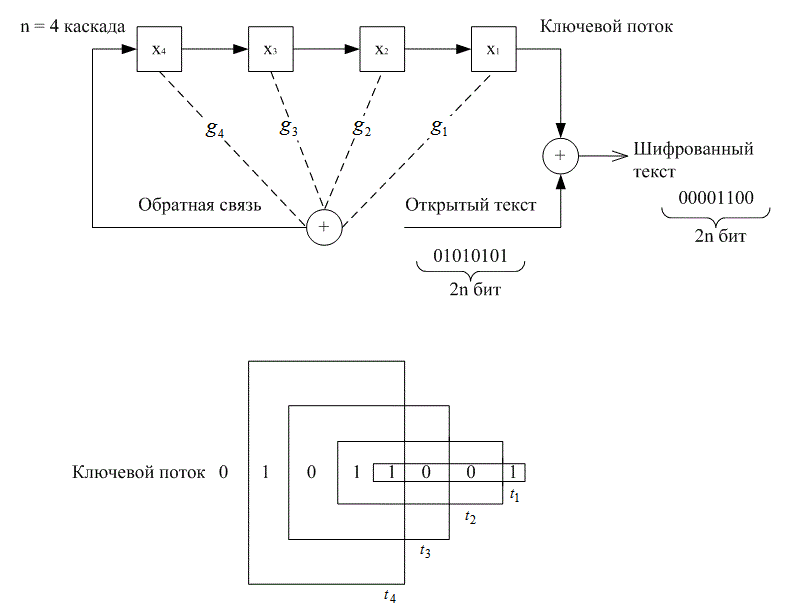
Рис. 14.14. Пример уязвимости линейного регистра сдвига с обратной связью

Здесь x5 — цифра, которая через контур обратной связи подана обратно на вход, а gi (i= 1 или 0) определяет i-e соединение обратной связи. Таким образом, изучая содержание регистра в четыре момента времени, изображенных на рис. 14.14, можно написать следующие четыре уравнения с четырьмя неизвестными.

g4 (1) + g3 (0) + g2 (0) + g1 (1) = 1

g4 (1) + g3 (1) + g2 (0) + g1 (0) = 0

g4 (0) + g3 (1) + g2 (1) + g1 (0) = 1 (14.28)

g4 (1) + g3 (0) + g2 (1) + g1 (1) = 1

Решение уравнений (14.28), соответствующих регистру, изображенному на рис. 14.13, является g1 = l, g2 = l, g3 = 0, g4 = 0. Таким образом, криптоаналитик узнал связи регистра, а также его начальное состояние в момент t1. Следовательно, он может узнать последовательность в любой момент времени [3]. Обобщив этот пример на любой регистр сдвига с п разрядами, можно переписать уравнение (14.27) следующим образом.

(14.29)

Уравнение (14.29) можно записать в матричной форме.

х = Хg (14.30)

где

x = g =

и

Х = .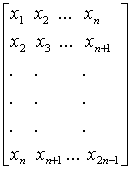

Можно показать [3], что столбцы X линейно независимы; таким образом, матрица X невырождена (ее определитель отличен от нуля) и имеет обратную. Следовательно,

g = X^-1 x (14.31)

Обращение матрицы требует порядка n³ операций и, таким образом, легко выполняется на компьютере для любого разумного значения п. Например, если n = 100, то n³ = 10⁶, и компьютеру со скоростью работы одна операция за 1 мкс для обращения матрицы понадобится 1с. Слабость регистра сдвига с обратной связью обусловлена линейностью уравнения (14.31). Использование нелинейной обратной связи в регистре сдвига делает задачу криптоаналитика гораздо сложнее, если не вычислительно трудноосуществимой.

14.4.3. Синхронные и самосинхронизирующиеся системы поточного шифрования

Системы поточного шифрования можно разделить на синхронные и самосинхронизирующиеся. В первых ключевой поток генерируется независимо от сообщения; так что потеря символа во время передачи неизбежно требует повторной синхронизации передачи и генераторов ключей приёмника. Синхронный поточный шифр изображен на рис. 14.15. Начальное состояние генератора ключа инициализируется с помощью известного входа I0. Шифрованный текст получается путем сложения по модулю 2 i-го символа ключа ki и i-го символа сообщения mi. Такие синхронные шифры обычно создаются для смешения, но не диффузии. Иными словами, шифрование символа не распространяется вдоль некоторого блока сообщения. По этой причине синхронные поточные шифры не имеют накопления ошибки.

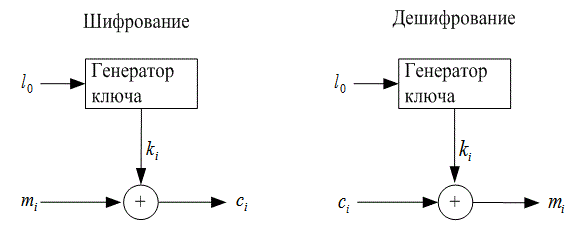
Рис. 14.15. Синхронный поточный шифр

При самосинхронизирующемся поточном шифре каждый ключевой символ определяется из фиксированного числа п предшествующих символов шифрованного текста (отсюда и название обратная связь по шифру). В таких системах происходит следующее: если символ шифрованного текста теряется во время передачи, ошибка накапливается для п символов, но после получения n верных символов шифрованного текста система восстанавливается.

В разделе 14.1.4 приводился пример обратной связи для шифрования с помощью автоматического ключа Вигнера. Показывалось, что преимуществом такой системы является: (1) генерация неповторяющегося ключа и (2) диффузия статистик открытого сообщения в шифрованном тексте. В то же время был и недостаток — ключ проявлялся в шифрованном тексте. Этой проблемы можно избежать, если при получении ключа пропустить символы шифрованного текста через нелинейный блок шифрования. На рис. 14.16 изображен регистр сдвига генератора ключа, работающий в режиме обратной связи по шифру. Каждый выходной символ шифрованного текста сi (образованный путем сложения по модулю 2 символа сообщения mi и символа ключа ki) подается обратно на вход регистра сдвига. Как и ранее, инициализация происходит с помощью известного входа I0. При каждой итерации выход регистра сдвига используется как вход (нелинейного) блочного алгоритма шифрования ЕВ. Символ младшего разряда на выходе ЕB становится следующим символом ключа ki+1, который используется в следующем символе сообщения mi+1. Поскольку после нескольких первых итераций вход алгоритма зависит только от шифрованного текста, система является самосинхронизирующейся.

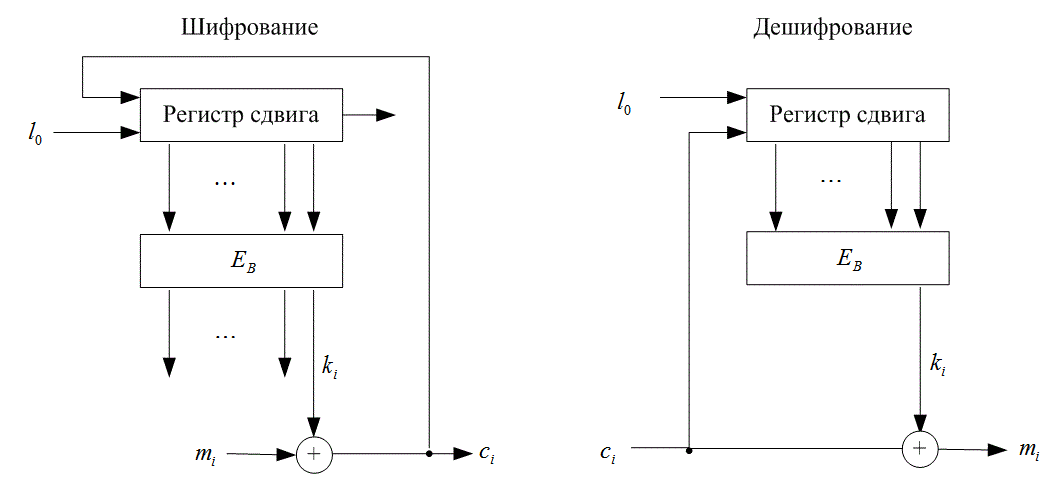
Рис. 14.16. Шифрование в режиме обратной связи