Передача непрерывных (аналоговых) сигналов по линии связи предполагает передачу бесконечного множества их мгновенных значений на протяжении конечного промежутка времени. При этом спектр финитного, т.е. ограниченного во времени, непрерывного сигнала бесконечен. Однако, на практике различные радиотехнические устройства (фильтры, усилители и другие) имеют ограниченную полосу пропускания, что приводит к ограничению спектра сигнала некоторой граничной частотой (или ), которая определяется свойствами получателя сообщений. Так например, общепринятой нормой в системах передачи речевых сигналов является ограничение спектра сигнала в пределах , в системах телевидения – . Как преодолеть противоречие между ограничением спектра сигнала и конечным временем его существования? Ответ на этот вопрос даёт теорема, сформулированная и доказанная академиком В.А. Котельниковым и получившая название теоремы Котельникова или теоремы отсчётов.

Теорема Котельникова формулируется следующим образом. Непрерывный сигнал , ограниченный по спектру частотой (или), полностью определяется совокупностью мгновенных значений (отсчётов) в моменты времени , отстоящие друг от друга на интервал времени .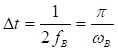

Математически теорема Котельникова определяется выражением

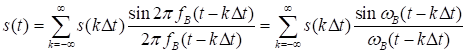, (3.1)

или с учётом (2.12)

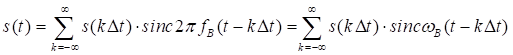, (3.2)

которое представляет собой разложение сигнала в особого рода ряд по системе базисных функций

,

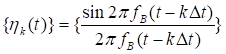являющихся ортогональными на интервале времени (сравните с разложением сигнала в ряд Фурье).

Доказательство теоремы Котельникова приведено в литературе [1]. Мы же остановимся на вопросах физического толкования и практического применения результатов теоремы.

Выделим одно из слагаемых ряда (3.1)

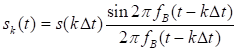. 3.3)

Это слагаемое представляет собой отклик идеального фильтра нижних частот (ФНЧ), т.е. фильтра с постоянным коэффициентом передачи в пределах полосы частот от нуля до , на очень короткий импульс с амплитудой . (рис. 3.1).

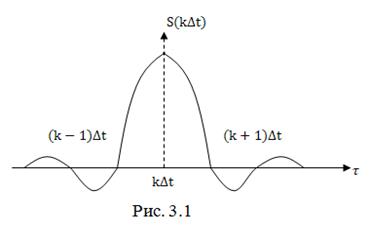
Отметим, что в моменты времени , и т.д. значения отклика равны нулю. Это определяет механизм восстановления непрерывного сигнала по его отсчётам.

Формирование последовательности отсчётов непрерывного сигнала, которая представляет собой дискретный сигнал, т.к. значение любого отсчёта сохраняется неизменным в течение интервала времени (см. классификацию сигналов), осуществляется при помощи импульсного модулятора.

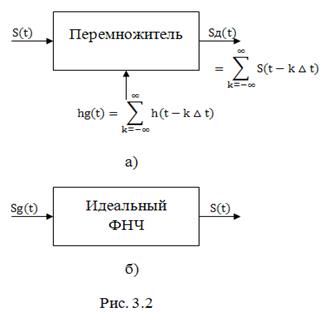Простейший вариант импульсного модулятора представляет со­бой перемножитель (рис. 3.2), на один вход которого подаётся непре­рывный сигнал , а на второй – последовательность

коротких единичных импульсов вида (1.13), следующих друг за другом с периодом (рис. 3.2, а). Тогда на выходе перемножителя будет иметь место последовательность коротких импульсов

,

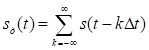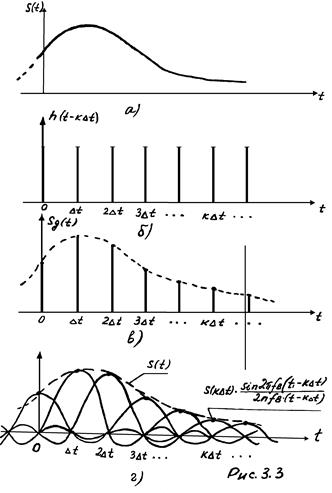амплитуды которых равны , т.е. соответствуют мгновенным значениям сигнала , отсчитанным в момент времени . (рис 3.3, в).

Процесс формирований последовательности отсчётов называется дискретизацией непрерывного сигнала.

Восстановление непрерывного сигнала осуществляется путём подачи дискретного сигнала на идеальный фильтр нижних частот. Отклик фильтра на каждый отсчёт определяется выражением (3.2). При этом, в момент времени , значение отклика определяется только k -тым отсчётом дискретного сигнала; отклик на остальные отсчёты равны нулю (Рис. 3.3, г). Суммируясь, эти отклики дают на выходе ФНЧ исходный сигнал .

Отметим два важных обстоятельства.

Во-первых, точное восстановление сигнала имеет место только при 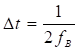. Введя в рассмотрение частоту дискретизации , получим так называемую частоту Найквиста, т.е. минимальное значение частоты дискретизации, при котором возможно точное восстановление непрерывного сигнала. Обычно, на практике частоту дискретизации выбирают выше предела Найквиста. Так, например, частота Найквиста для речевого сигнала при составляет . В реальных РТИС эта частота составляет .

Во-вторых, точное восстановление сигнала возможно при суммировании бесконечного числа откликов, что соответствует сигналу , неограниченному во времени. Но в действительности, сигналы являются ограниченными и по спектру и по времени. Однако, при определённых допущениях теорема Котельникова справедлива и для этого случая.

Если сигнал, длительностью ограничивается радиотехническим устройством с граничной частотой , то для его представления в дискретной форме требуется конечное число отсчетов, где

. (3.4)

Таким образом для восстановления сигнала длительностью , ограниченного по спектру частотой достаточно передать независимых отсчетов, однозначно связанных с его формой.

Но теоретически сигнал, ограниченный по времени имеет бесконечный спектр. А это означает, что при восстановлении сигнала по отсчетам будет иметь место ошибка, т.е. восстановленный сигнал ŝ(t) будет отличаться от исходного . Казалось бы, теорема Котельникова неприменима к реальным сигналам. Тем не менее, если к точности восстановления сигнала по отсчетам предъявить определенные требования, например, допустить его восстановление с заданным уровнем ошибки, то утверждения теоремы Котельникова можно с успехом распространить на реальные сигналы, несколько изменив частоту дискретизации по сравнению с пределом Найквиста.

Теперь с учетом того, что реальный сигнал длительностью представляется отсчетами мгновенных значений, выражение (3.1) принимает вид:

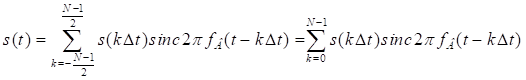. (3.5)

Величина называется базой сигнала . Понятие базы играет важную роль при представлении непрерывного сигнала конечным числом отсчетов. Соответствующим образом выбранная база определяет информационные показатели сигналов, способность противостоять помехам при передаче по каналам связи, энергетическую скрытность и другие.

Рассмотрим теперь вопрос оценки точности восстановления непрерывного сигнала по совокупности отсчетов его мгновенных значений. Как уже неоднократно подчеркивалось выше, ограниченный во времени сигнал имеет бесконечный спектр. Согласно равенству Парсеваля (2.50) энергия такого сигнала равна

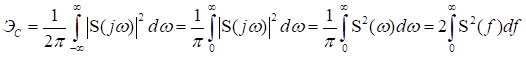, 3.6)

где или – энергетический спектр, представленный как функция либо круговой , либо циклической частоты.

Энергия за пределами частоты (или ) составляет величину

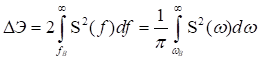. (3.7)

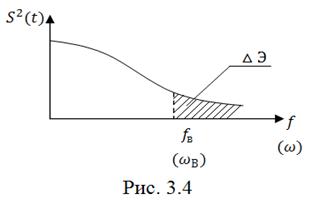
На рис. 3.4 изображен энергетический спектр сигнала, ограниченного во времени и граничная частота .

Площадь под всей кривой характеризует полную энергию сигнала , а площадь заштрихованного участка - ту часть энергии , которая сосредоточена за пределами .

Тогда отношение

(3.8)

может служить оценкой точности восстановления сигнала. Задаваясь величиной можно определить частоту , а следовательно и частоту дискретизации .

Рассмотрим следующий пример. Пусть сигнал на интервале времени описывается экспоненциальной функцией

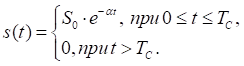
Воспользовавшись преобразованием Фурье, найдем спектральную функцию сигнала

.

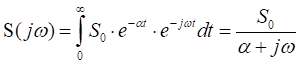Модуль спектральной функции

,

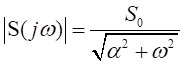а энергетический спектр

.

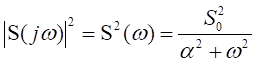Воспользовавшись выражением (3.5), найдем энергию сигнала

.

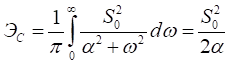В соответствии с (3.6), вычислим :

.

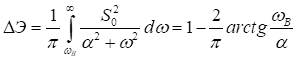При расчете и использован табличный интеграл

.

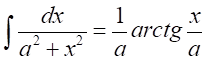Найдем величину среднеквадратичной ошибки восстановления

.

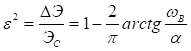Представим

.

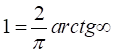Тогда

,

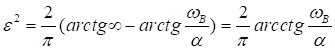откуда следует

.

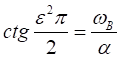Полагая, что для малых значений

,

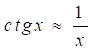получим

.

Теперь можно найти

,

или переходя к циклическим частотам

.

Частота дискретизации

.

Таким образом, задаваясь величиной можно определить частоту дискретизации непрерывного сигнала. Очевидно, число отсчетов при дискретизации рассматриваемого сигнала будет равно

.

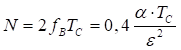Из приведенного примера следует, что чем меньшую ошибку восстановления требуется обеспечить, тем выше должна быть частота дискретизации.

Теорема Котельникова устанавливает однозначное соответствие между аналоговым сигналом и отсчетами его мгновенных значений во временной области. Оказывается, можно сформулировать теорему отсчетов и в частотной области. При этом примем во внимание, что комплексный спектр одиночного сигнала длительностью является сплошным. Тогда имеет место следующее утверждение. Спектральная функция сигнала , ограниченного во времени величиной полностью определяется совокупностью отсчетов , отстоящих друг от друга на частотный интервал 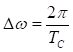, т.е.

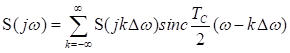. (3.9)

Теорема отсчетов в частотной области основывается на свойстве симметрий преобразований Фурье относительно переменных (или ) и . Суть этого свойства состоит в том, что преобразование Фурье периодического сигнала с периодом приводит к линейчатой (дискретной) спектральной функции, где отдельные спектральные составляющие (см. подраздел 2.1) отстоят друг от друга по оси частот на величину (или ), и наоборот, преобразование Фурье периодической спектральной функции с периодом приводит к дискретной временной функции с периодом .

Исходя из этого свойства, если в (3.2) заменить на ; на , а на , то в результате получим выражение (3.9). Как и в случае разложения сигнала в ряд Котельникова, разложение его спектра ограничивается отсчетами. Тогда выражение (3.5) в частотной области принимает вид

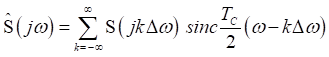. (3.10)

Казалось бы, для восстановления спектральной функции по совокупности отсчетов , необходимо знать отсчетов модуля и отсчетов аргумента комплексных величин . Однако, если учесть, что модуль спектра , т.е. амплитудный спектр является четной функцией, а аргумент , т.е. фазовый спектр – нечетной функцией, то число независимых отсчетов сокращается вдвое и составляет , т.е. равно базе сигнала.

Подводя итог вышеизложенному, отметим, что теорема Котельникова устанавливает принципиальную возможность представления непрерывного сигнала последовательностью его мгновенных значений. Такую операцию иногда называют импульсным преобразованием непрерывного сигнала. Такое преобразование лежит в основе импульсных методов передачи сообщений в радиотехнических системах. Более того, дискретизация непрерывных сигналов в соответствии с теоремой Котельникова является промежуточной операцией при формировании цифровых сигналов, которые в настоящее время нашли самое широкое распространение как в радиотехнических системах передачи сообщений, так и радиоэлектронных системах обработки, отображения и регистрации информации, и во многих других областях.