4.6.1. Квадратурная реализация модулятора

4.6.2. Пример модулятора D8PSK

4.6.3. Пример демодулятора D8PSK

Описание реальных модуляторов и демодуляторов облегчается при использовании комплексной формы записи, введенной в разделе 4.2.1. Любой реальный полосовой сигнал s(t) можно представить в комплексной форме как

(4.57)

где g(t) — комплексная огибающая (complex envelop), которую можно записать следующим образом.

(4.58)

Амплитуда комплексной огибающей выражается как

, (4.59)

а фаза определяется следующим образом.

(4.60)

В формуле (4.57) g(t) можно называть полосовым сообщением или данными в комплексной форме, а — несущей в комплексной форме. Произведение этих двух величин представляет операцию модулирования, a s(t), действительная часть произведения, — это переданный сигнал. Следовательно, используя формулы (4.4), (4.57) и (4.58), s(t) можно выразить следующим образом.

(4.61)

Отметим, что модулирование сигналов, выраженное в общей форме (а + ib), умноженное на (с + id), дает сигнал с переменой знака (в квадратурном члене несущей волны) вида ас - bd.

4.6.1. Квадратурная реализация модулятора

Рассмотрим узкополосный сигнал g(t), который представлен последовательностью идеальных импульсов x(t) и y(t), передаваемых в дискретные моменты времени k = 1,2,.... Таким образом, g(t), x(t) и y(t) в уравнении (4.58) можно записывать как gk, xk и yt. Пусть значения амплитуд импульсов равны xk=yk=0,101A. При этом комплексную огибающую можно выразить в дискретной форме следующим образом.

(4.62)

Из комплексной алгебры знаем, что , но с практической точки зрения i можно рассматривать как "метку", напоминающую, что мы не можем использовать обычное сложение при группировке членов в формуле (4.62). Далее мы будем рассматривать синфазную и квадратурную модуляции, xk и yt, как упорядоченную пару. Модулятор, реализованный по квадратурному принципу, показан на рис. 4.21, где можно видеть, что импульс xk умножается на (синфазный компонент несущей), а импульс yt — на (квадратурный компонент несущей). Процесс модулирования можно кратко описать как умножение комплексной огибающей на с последующей передачей действительной части произведения. Итак, записываем следующее.

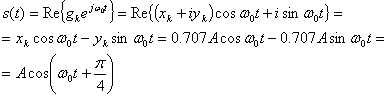(4.63)

Снова напомним, что квадратурный член несущей включает перемену знака в процессе модуляции. Если в качестве опорного сигнала использовать , то при передаче сигнала s(t) (уравнение (4.63)) происходит сдвиг опоры на π/4. Если же в качестве опорного сигнала применить , то переданный сигнал s(t) в уравнении (4.63) приводит к запаздыванию опоры на π/4. Графическая иллюстрация сказанного приведена на рис. 4.22

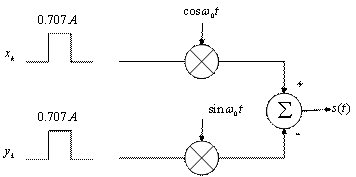
Рис. 4.21. Модулятор работающий по квадратурному принципу

4.6.2. Пример модулятора D8PSK

На рис. 4.23 изображена квадратурная реализация модулятора дифференциальной восьмифазной манипуляции (differential 8-PSK — D8PSK). Поскольку модуляция является 8-ричной, каждому информационному вектору , который можно записать как

(4.64)

присваивается 3-битовое сообщение (xk, yk, zk).

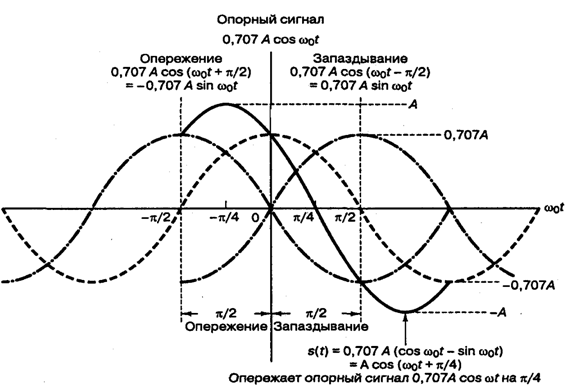
Рис. 4.22. Опережение/запаздывание синусоид

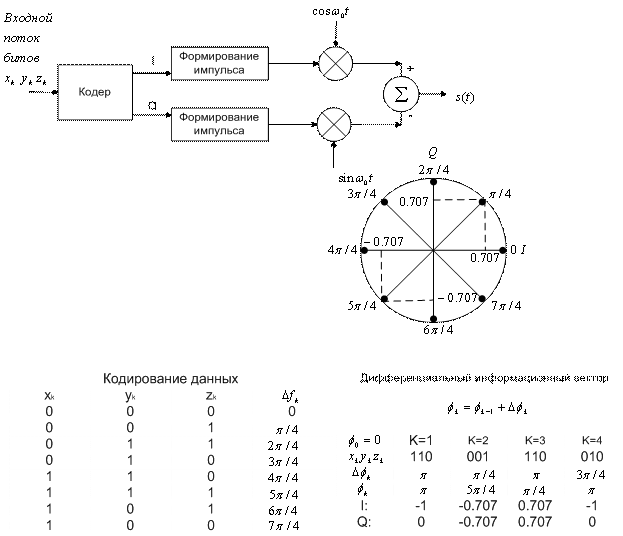
Рис. 4.23. Квадратурная реализация модулятора D8PSK

Сложение текущего кодируемого сообщения, выраженного разностью фаз с предыдущей фазой обеспечивает дифференциальное кодирование сообщений. Последовательность векторов, созданная с использованием уравнения (4.64), подобна результатам дифференциального кодирования, полученного с помощью процедуры, описанной в разделе 4.5.2. Можно заметить (рис. 4.23), что в результате кодирования 3-битовых последовательностей сообщений разностями фаз получаем не двоичную последовательность от 000 до 111, а специальный код, называемый кодом Грея (Gray code). (Преимущества использования подобного кода приведены в разделе 4.9.4.)

Пусть на вход модулятора, изображенного на рис. 4.23, в моменты времени k= 1, 2, 3, 4 поступают информационные последовательности 110, 001, 110, 010. Далее используем таблицу кодирования данных, приведенную на рис. 4.23, формулу (4.64) и, кроме того, положим начальную фазу (момент времени k = 0) равной нулю: = 0. В момент времени k = 1 дифференциальная информационная фаза, соответствующая набору = 110, равна = 4π/4 = π. Считая амплитуду вращающегося вектора единичной, синфазный (I) и квадратурный (Q) узкополосные импульсы равны -1 и 0. Как показано на рис. 4.23, форму этих импульсов обычно задает фильтр (такой, как фильтр с характеристикой типа приподнятого косинуса).

Для момента k = 2 таблица на рис. 4.23 показывает, что сообщение 001 кодируется сдвигом фаз = π/4. Следовательно, согласно формуле (4.64), вторая дифференциальная информационная фаза равна , и в момент k=2 синфазный и квадратурный узкополосные импульсы равны, соответственно, xk = -0,707 и yk = -0,707. Переданный сигнал имеет вид, приведенный в формуле (4.61).

(4.65)

Для сигнального множества, которое может представляться в координатах "фаза-амплитуда", такого как MPSK или MQAM, уравнение (4.65) позволяет сделать интересное наблюдение. Из него видно, что квадратурная реализация передатчика сводит все типы передачи сигналов к единственной амплитудной модуляции. Каждый вектор на плоскости передается посредством амплитудной модуляции его синфазной и квадратурной проекций на синусоидный и косинусоидный компоненты его несущей. В каждом случае процесс формирования импульса считается идеальным, т.е. предполагается, что информационные импульсы имеют идеальные прямоугольные формы. Таким образом, используя уравнение (4.65) для момента k = 2, при xk = -0,707 и yk = -0,707, можно записать переданный сигнал s(t) следующим образом.

(4.66)

4.6.3. Пример демодулятора D8PSK

В предыдущем разделе описание квадратурной реализации модулятора начиналось с умножения комплексной огибающей (узкополосного сообщения) на с последующей передачей действительной части произведения s(t), описанного в формуле (4.63). Демодулятор подобной схемы включает обратный процесс, т.е. умножение принятого полосового сигнала на с целью восстановления узкополосного сигнала. В левой части рис. 4.24 в упрощенном виде показан модулятор, изображенный на рис. 4.23, и сигнал , переданный в момент времени k = 2 (продолжаем использовать пример, описанный в предыдущем разделе). В правой части рис. 4.24 показана квадратурная реализация демодулятора.

Рис. 4.24. Пример модулятора/демодулятора

Отметим тонкое отличие между членом в модуляторе и демодуляторе. В модуляторе знак "минус" появляется при определении действительной части комплексного сигнала (произведения комплексной огибающей и комплексной несущей). В демодуляторе член появляется при умножении полосового сигнала на сопряженное несущей модулятора. Демодуляция является когерентной, если фаза восстанавливается. Для упрощения записи основных соотношений процесса мы пренебрегаем шумом. Итак, после синфазного умножения в демодуляторе на в точке А получаем следующий сигнал.

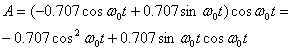(4.67)

Используя тригонометрические соотношения, приведенные в формулах (Г.7) и (Г.9), получаем следующее.

(4.68)

После фильтрации с использованием фильтра нижних частот (low-pass filter — LPF) в точке А' восстанавливается идеальный отрицательный импульс.

(с точностью до масштабного коэффициента) (4.69)

Подобным образом после квадратурного умножения в демодуляторе на в точке В получаем сигнал.

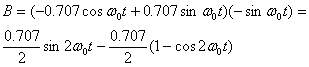(4.70)

После прохождения сигналом фильтра нижних частот в точке В' восстанавливается идеальный отрицательный импульс.

(с точностью до масштабного коэффициента) (4.71)

Таким образом, видим, что в точках A' и В' (идеальные) дифференциальные информационные импульсы для синфазного и квадратурного каналов равны -0,707. Поскольку модулятор/демодулятор является дифференциальным, для нашего примера k=2 получаем следующее.

(4.72)

Будем считать, что в предыдущий момент времени k = 1 демодулятор правильно определил, что фаза сигнала равна π. Тогда из формулы (4.72) можем получить следующее.

(4.73)

Вернувшись к таблице модуляции на рис. 4.23, видим, что данной фазе соответствует информационная последовательность = 001, что совпадает с данными, посланными в момент времени k = 2.