2.1. Вектор. Линейные операции над векторами
2.1.1. Геометрический вектор. Понятие вектора
2.1.2. Линейные операции над векторами
2.1.3. Линейная зависимость векторов, теоремы о линейной зависимости
2.2.1. Скалярное произведение векторов
2.1. Вектор. Линейные операции над векторами
2.1.1. Геометрический вектор. Понятие вектора
Вектор:
отрезок с началом в точке А и концом в точке В.
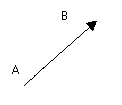 Обозначается:
Обозначается: ![]()
Два вектора ![]() равны, если они совпадают при параллельном переносе.
равны, если они совпадают при параллельном переносе.
Два вектора называются коллинеарными, если они параллельны.
Три вектора называются компланарными, если они лежат в одной плоскости.
2.1.2. Линейные операции над векторами
А) Умножение вектора на число.
Б) Сложение векторов
1) ![]()
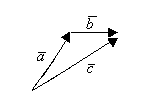
![]()
2) ![]()
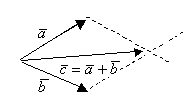
![]()
3) ![]() - длину вектора умножить на
- длину вектора умножить на ![]() и оставить направление вектора если
и оставить направление вектора если ![]()
Таким образом операции обладают св-ми.
1) ![]()
2) ![]()
Вектор у которого начало и конец совпадают есть нулевой вектор ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
Вычитание - обратное сложению.
2.1.3. Линейная зависимость векторов, теоремы о линейной зависимости
Определение 1. Система векторов ![]() называется линейно зависимой, если сущ. числа
называется линейно зависимой, если сущ. числа ![]() не все равные 0, такие что
не все равные 0, такие что ![]() (1)
(1)
Система векторов![]() называется линейно независимой, если равенство (1) возможно только в том случае, когда все числа
называется линейно независимой, если равенство (1) возможно только в том случае, когда все числа ![]() =0
=0
Выражение стоящее в левой части рав-ва (1) наз-ют линейной комбинацией векторов ![]()
Определение 2. Система векторов является линейно зависимой, если существует линейная комбинация этих векторов с неравными 0 числами, которая тождественно равна.
Теорема 1. Если система векторов ![]() содержит нулевой вектор, то данная система линейно зависима.
содержит нулевой вектор, то данная система линейно зависима.
Доказательство. Пусть ![]() , тогда
, тогда ![]()
![]()
![]()
Теорема 2. Если к системе линейно зависимых векторов ![]() добавить произвольный вектор
добавить произвольный вектор ![]() , то вновь полученная система будет линейно зависима.
, то вновь полученная система будет линейно зависима.
Доказательство. Т.К. система векторов ![]() линейно зависима, то есть
линейно зависима, то есть ![]() не все равные нулю, такие что
не все равные нулю, такие что ![]() (2)
(2) ![]() (3)
(3)
![]() (4)
(4)
Есть ![]() ,
,![]()
![]() 0 - не все равны нулю
0 - не все равны нулю
Следовательно система линейно зависима.
Следствие. Если к линейно зависимой системе добавить любое кол-во векторов, то полученная система будет линейно зависима.
2.1.4. Теорема о линейной зависимости двух векторов
Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство. ![]()
![]()
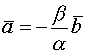
![]() - коллинеарны
- коллинеарны
Теорема. Три вектора линейно зависимы тогда и только тогда, когда они компланарны
Доказательство. ![]()
![]()
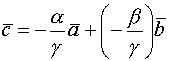
![]()
![]()
Для ![]() и
и ![]() пл-ть
пл-ть ![]() , что
, что ![]() (или
(или
//) и ![]()
![]()
![]()
![]()
![]() либо
либо ![]() ,
,
либо // ей ![]() они компланарны.
они компланарны.
Теорема. В трехмерном пространстве любые 4 вектора линейно зависимы.
Доказательство.
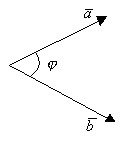
![]()
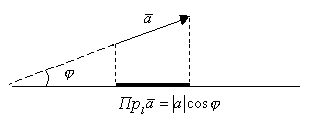
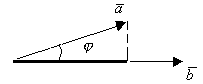
![]() -угол между
-угол между![]()
Вектор в системе координат
Базис-максимальная упорядоченная система линейно независимых векторов.
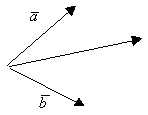
![]()
На плоскости 2 любых неколлинеарных вектора образуют базис.
ДПБ-базис, состоящий из ортогональных единичных векторов.
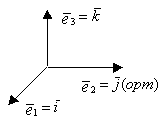
Операции над векторами в координатной форме.
![]()
![]()
![]()
![]()
![]()
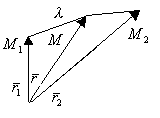
![]()
![]()
![]()
![]()
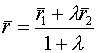
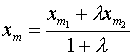
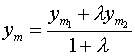
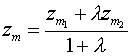
![]() -нач.точка
-нач.точка ![]() - кон.точка
- кон.точка
![]()
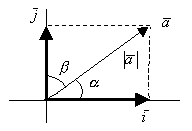
![]()
![]()
направляющие косинусы
![]()
![]()
2.2. Произведение векторов
2.2.1. Скалярное произведение векторов
Определение. Скалярным произведением векторов наз-ся скалярное произведение длин этих векторов на косинус угла между ними. ![]()
Если вектор нулевой, то все произведения - ноль
Свойства скалярного произведения
-
- Если
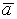 и
и 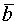 ортогональны
ортогональны 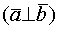 ,
,
то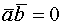
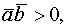 если
если 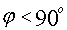 ;
; 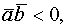 если
если 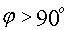
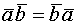 (коммутативность)
(коммутативность)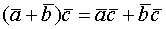 (дистрибутивность)
(дистрибутивность)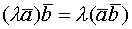
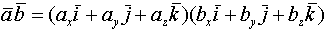 =
=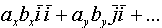 =
=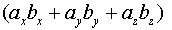
- Если
(скалярное произведение в координатах)
Условие ортогональности векторов ![]()
Условие коллинеарности векторов 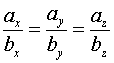
Скалярный квадрат ![]()
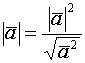
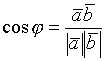
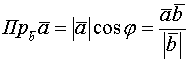
2.2.2. Векторное произведение векторов
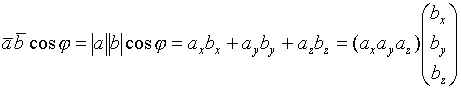
Ориентация базиса
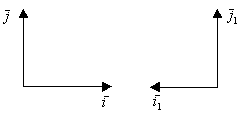
Декартов прямоугольный базис на плоскости
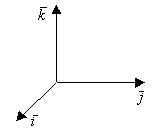
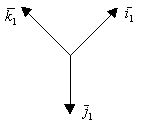 Декартов прямоугольный базис в пространстве
Декартов прямоугольный базис в пространстве
Правой тройкой векторов называется такая тройка, что если смотреть с конца вектора ![]() , то поворот от
, то поворот от ![]() происходит в положительном направлении (против часовой стрелки).
происходит в положительном направлении (против часовой стрелки).
Определение: Векторным произведением, ![]() 2-х векторов называется вектор
2-х векторов называется вектор ![]() , такой что
, такой что
1) ![]() - правая тройка
- правая тройка
2) ![]()
3) ![]()
Свойства векторного произведения
-
- Если 2 вектора коллинеарны, их произведение =0
![]()
-
- Если поменять местами сомножители, меняется знак
![]() (антикоммутативность)
(антикоммутативность)
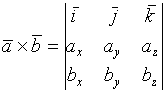
Пример.
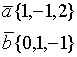
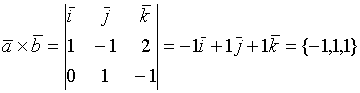
2.2.3. Смешанное произведение векторов
![]()
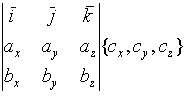 =
=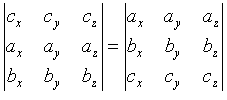 =
=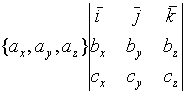 =
=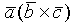
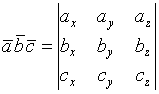
Свойства смешанного произведения