1. В основе соотношений неопределённостей лежит корпускулярно-волновая двойственность свойств частиц. Возможность задавать для частицы лишь вероятность пребывания в данной точке приводит к тому, что классические понятия координаты частицы, импульса могут применяться лишь в переделах, установленных соотношениями неопределённостей.

.

В этих формулах характеризуют неопределённости в координатах частицы, а - пределы, в которых могут быть заключены проекции импульса частицы на оси. Чем точнее заданы координаты частицы, тем более неопределены компоненты её импульса.

2. Так как то уравнения, связывающие неопределенности координат и импульса, примут вид:

.

3. Аналогичное соотношение неопределённостей существует между энергией W и временем t. Если частица некоторое время находится в нестационарном (например, возбуждённом) состоянии, то энергия W этого состояния может быть определена лишь с точностью до величины . Неопределённость энергии связана со временем соотношением:

.

4. Шириной Г энергетического уровня называется неопределённость энергии квантовомеханической системы (атома, молекулы и др), обладающей дискретными уровнями энергии W_k в состоянии, которое не является строго стационарным. Например, если электрон в атоме находится в возбуждённом состоянии, то размытие уровня энергии и называется уширением уровня . Значение ширины уровня Г связано со средним временем t пребывания системы в возбуждённом состоянии соотношением неопределённостей:

.

Для строго стационарного состояния . Ширина уровня может быть и очень малой по сравнению с энергией уровня (например, для ядра при -распаде), и сравнимой со значениями расстояний между энергетическими уровнями (например, для возбуждённых ядер, испускающих нейтроны при квантовых переходах). Ширина уровня пропорциональна сумме вероятностей всех возможных переходов с этого уровня - и спонтанных , и вызванных различными следствиями.

5. Ширина энергетического уровня Г определяет ширину спектральной линии. Зависимость интенсивности I испускания или поглощения от частоты обычно имеет максимум при частоте перехода (рисунок 1), которая определяется соотношением:

,

где - энергии состояний, между которыми происходят переходы.

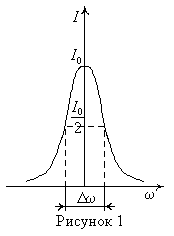
Шириной (полушириной) спектральной линии называют интервал частот отсчитываемый по кривой зависимости интенсивности от частоты при значении интенсивности, равной половине максимальной интенсивности . Так как длина волны и частоты излучения связаны соотношением , то ширину спектральной можно характеризовать интервалом длин волн , учитывая, что:

.

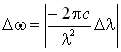Уширение отражает степень немонохроматичности спектральных линий и связано со временем жизни атомной системы в состояниях, характеризуемых квантовыми числами n и k.

,

где - естественная ширина спектральной линии. Для установления немонохроматичности ограниченного цуга волн (атом излучает свет в виде отдельных импульсов - цугов волн) следует пользоваться соотношением неопределённостей в виде, отличном от формул (17-20).

,

где - длительность излучения, - ширина спектра.

Пространственная протяжённость цуга волн в вакууме задаётся соотношением:

,

где с = 3 × 10⁸ м/с - скорость света в вакууме.

Чем короче цуг волн, тем шире его спектр, т.е., тем сильнее цуг отличается от монохроматической волны (сравните с волновым пакетом).

6. С помощью соотношений неопределённостей можно оценить минимальную энергию частицы в любом силовом поле U=U(r).Для этого необходимо записать полную энергию частицы в виде суммы кинетической и потенциальной:

.

Затем воспользоваться соотношением неопределённостей координаты и импульса. Для центрально-симметричного поля эту формулу можно переписать в виде . С учётом того, что частица квантовая, надо сделать приближения ~ p, ~ r, найти зависимость энергии частицы от координат:

и исследовать эту функцию на экстремум, определив наименьшую возможную координату, а затем и минимальную энергию.

Если силовое поле симметрично относительно некоторой оси (например, ), то следует неопределённость в координате полагать равной двойному значению координаты .