4.1. Реляционная модель данных
4.2. Основные операции реляционной алгебры
4.3. Переход от ER-диаграмм к системе отношений (таблиц)
4.4. Понятие первичного и внешнего ключа
4.5. Ограничительные условия, поддерживающие целостность
4.1. Реляционная модель данных
Реляционная модель данных – это такая модель данных, в которой данные представлены в виде таблиц.

Основные понятия реляционной МД.
Атомарное значение – неделимое значение.
Домен – множество атомарных значений одного и того же типа. Если значения принадлежат одному и тому же домену, то имеет смысл их сравнение. А1, А5, А7, Аi – атрибуты отношения, т.е. набор значений принадлежащих к одному и тому же домену.
Заголовок (схема отношений) – это набор его атрибутов.
Математическое определение отношений. Если V1, V2…, Vi – это набор множеств именуемых доменами, тогда отношение R (V1, V2, .., Vi) представляет собой подмножество декартовых произведений доменов (V1*V2*…*Vi). Каждому домену приписывается имя, в качестве отношения рассматривается отношение этих имён. Элементом отношения является кортеж.
Кортеж – это множество пар имён атрибутов, значений атрибутов (это строка таблицы).
Мощность отношения – это число его кортежей.
Степень отношения – это число его атрибутов (число столбцов в таблице).
Возможный ключ отношения – это минимальный набор атрибутов, который однозначно определяет кортеж. У ключа есть 2 свойства: уникальность и минимальность.
Уникальность – значения ключевых атрибутов не могут повторяться.
Минимальность – ни один из атрибутов не может быть исключён из набора без нарушения уникальности.
Свойства отношений:
- Отношение имеет своё уникальное имя.
- Уникальность имён атрибутов.
- Отсутствие кортежей-дубликатов.
- Атомарность значений атрибутов.
- Отсутствие упорядоченности атрибутов и кортежей.
4.2. Основные операции реляционной алгебры
В реляционной алгебре в качестве операндов используются отношения. В результате этих операций возникают новые отношения.
Условные обозначения:
X, Y – отношения-операнды.
R – отношение-результат.
Mx, My, Mr – мощности отношений X,Y,R.
А, B – подмножества схем отношений.
Все операции можно разбить на 2 группы:
- Теоретико-множественные.
- Операции, учитывающие структуру решений как модель данных.
-
- Объединение.
R=X+Y
Max(Mx,My) ≤ Mr ≤ Mx+My
Схемы кортежей и операндов должны быть одинаковы. - Разность.
R=X-Y
0 ≤Mr ≤ Mx - Пересечение
R=X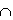 Y=X-(X-Y)
Y=X-(X-Y)
0 ≤ Mr ≤min(Mx,My) - Декартово произведение.
R=X*Y
Mr=Mx*My
- Объединение.
X:
|
A |
B |
|
15 |
7 |
|
8 |
11 |
Y:
|
W |
Z |
|
6 |
4 |
|
2 |
3 |
R=X*Y:
|
A |
B |
W |
Z |
|
15 |
7 |
6 |
4 |
|
8 |
11 |
6 |
4 |
|
15 |
7 |
2 |
3 |
|
8 |
11 |
2 |
3 |
-
- Проекция (ограничение).
R=X(A), где A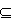 схема X.
схема X.
Результатом проекции является отношение со схемой А, где каждый кортеж составлен из значений соответствующего кортежа Х.
Пример:
- Проекция (ограничение).
Х:
|
Ф.И.О. |
Отдел |
должность |
Оклад |
|
Иванов |
ОГЭ |
Слесарь |
1000 |
|
Петров |
ОГМ |
Электрик |
2000 |
|
Сидоров |
ОГЭ |
Мастер |
3000 |
R=X(Ф.И.О.)
R:
|
Ф.И.О. |
|
Иванов |
|
Петров |
|
Сидоров |
Операция проекции обладает свойством собственности. Это значит, что 2 последовательных проекции могут быть заменены одной проекцией при соблюдении следующих условий:
![]()
- Селекция (выбор).
R=X(A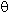 B), где А
B), где А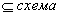 Х, В- множество констант,
Х, В- множество констант, 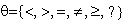
Нужно, чтобы А и В были сравнимы по смыслу с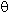 .
.
Для всякого Ai,j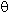 Bi,j должно иметь смысл.
Bi,j должно иметь смысл.
Результатом операции селекции является отношение, состоящее из тех кортежей Х, которые удовлетворяют заданным условиям. Селекция часто используется в комбинации с проекцией. - Деление.
R=X(B)Y; B![]() схема Y
схема Y
Результатом операции деления является минимальное множество кортежей таких, что декартово произведение этого множества с Y присутствует в X.
Y(B)![]() X
X
- R1=X(A-B)*Y(B)-X(A)
- R=X(A-B)-R1(A-B)
Пример: Найти преподавателя, который проводит занятия по каждой дисциплине.
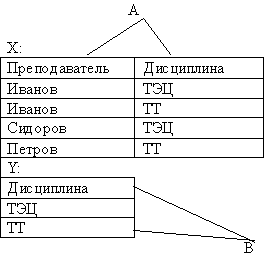
8. Соединение.
R=X(A![]() B)Y A
B)Y A![]() схема Х
схема Х
В![]() схема Y, или множество констант.
схема Y, или множество констант.
Результатом операции соединения является селекция по заданному условию декартова произведения операндов.
R1=X*Y R=R1(A![]() B)
B)
Пример: соединить отношения Х и У по условию W>5:
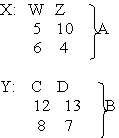
X(W>5)Y
R1: W Z C D W Z C D
5 10 12 13 6 4 8 7
6 4 8 7 6 4 12 13
5 10 8 7
6 4 12 13
9. Переименование.
Результатом переименования является тождественно равное отношение операндов, но с другим именем
Операции реляционной алгебры используются в запросах для поиска нужных данных в таблице.
4.3. Переход от ER-диаграмм к системе отношений (таблиц)
При создании системы отношений необходимо выполнить следующие условия:
- Информация в таблицах не должна повторяться.
- Поля таблиц не должны принимать неопределённых (пустых) значений.
ШАГ 1
- Преобразование сущностей. Каждая простая сущность становится таблицей.
- Каждый атрибут сущности становится столбцом в таблице.
- Уникальный идентификатор сущности становится первичным ключом таблицы.
- Если в ER-диаграмме присутствовали подтипы сущностей, они выносятся в отдельные столбцы.
ШАГ 2
Переход от ER-диаграмм к системе отношений.
|
Значность связи |
Членство |
Число таблиц |
|
1:1 |
Обязательная |
1 |
|
Возможная |
2 |
|
|
Необязательная |
3 |
|
|
1:m |
Обязательная |
2 |
|
Возможная |
2 |
|
|
Необязательная |
3 |
|
|
m:m |
Обязательная |
3 |
|
Возможная |
3 |
|
|
Необязательная |
3 |
4.4. Понятие первичного и внешнего ключа
Ключ – это минимальный набор атрибутов, который однозначно определяет кортеж.
Минимальность означает, что никакое подмножество атрибутов входящих в ключ не будет являться ключом.
Суперключ – это любой набор атрибутов, который однозначно определяет кортеж.
Составной ключ – это ключ, содержащий 2 или более атрибутов. Возможных ключей может быть много, но только один из них выбирается в качестве первичного.
Первичный ключ – это ключ наиболее удобный для поиска строк таблицы.
Внешний ключ – это набор атрибутов одного отношения, который является ключом другого отношения или того же самого отношения.
Рекурсивный внешний ключ – это внешний ключ, который ссылается на своё собственное отношение.
Набор схем отношений с определёнными первичными и внешними ключами называется схемой данных.
4.5. Ограничительные условия, поддерживающие целостность
Целостность – это согласованность данных в базе данных.
Ограничительные условия – это правила, которые определяют набор возможных значений в БД.
- Существует 2 вида целостности:
- Категорная целостность
- Целостность на уровне ссылок
Категория – это конкретный объект, информация о котором хранится в БД.
Правила категорной целостности заключаются в том, что никакой ключевой атрибут строки не может оставаться пустым.
При целостности на уровне ссылок каждое непустое значение внешнего ключа должно быть равно одному из текущих значений первичного ключа связанного с ним отношения.
Каскадное обновление – это автоматическое обновление данных в таблице при изменении данных связанных с ней.
4.6. Аномалии хранения данных
Аномалия обновления – это противоречивость данных, связанная с избыточностью и частичным обновлением.
Аномальное удаление – непреднамеренная потеря данных в связи с удалением других данных.
Аномалии ввода – это невозможность ввести данные в таблицу ввиду отсутствия других данных.
Декомпозиция – это разделение таблиц на 2 или несколько таблиц с целью устранения аномалий.
Подход создания БД с помощью декомпозиции называется аналитическим.
Синтетический способ – это способ, когда создаются таблицы сразу без аномалий.
4.7. Функциональная зависимость
R(X,Y) ; X,Y ![]() схема R.
схема R.
Если не может существовать более одного кортежа R, совпадающего по всем значениям из Х и отличающегося хотя бы по одному значению по Y, то зависимость называют функциональной зависимостью по Х.
Классификация функциональных зависимостей.
- Полная функциональная зависимость(ФЗ).
Y зависит от Х, но не зависит от любого подмножества Х. - Неполная ФЗ.
Y зависит от Х и от какого-нибудь подмножества Х. - Тривиальная ФЗ.
Y является подмножеством Х. - Транзитивная ФЗ.
R(X,Y,Z); X,Y,Z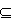 R
R
X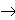 Z, Z
Z, Z 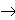 Y, X
Y, X 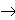 Y.
Y.
В этом случае Х функционально определяет Z, Z определяет Y, когда Х не определяет функцию Y. - Многозначная ФЗ.
Говорят, что в отношении R с наборами атрибутов X,Y,Z имеется многозначная ФЗ, если существует множество значений Z, соответствующее паре значений X и Y, которое зависит функционально от Y, но не зависит функционально от Z.
Правила вывода или аксиомы Армстронга.
Сформулируем правила вывода:
- Рефлексивность.
X,Y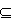 схема R
схема R
Если X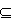 Y, то Y
Y, то Y 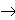 X.
X. - Присоединение.
X,Y,Z
W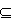 Z
Z
XZ=X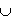 Z
Z
Если X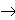 Y, то XZ
Y, то XZ 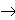 YW.
YW. - Транзитивность.
X,Y,Z
Если X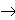 Y и Y
Y и Y 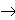 Z, то X
Z, то X 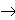 Z
Z - Псевдотранзитивность.
X,Y,Z,W
X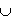 W=XW
W=XW
Y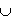 W=YW
W=YW
Если X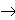 Y, XW
Y, XW 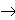 YW, YW
YW, YW 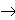 Z, то YW
Z, то YW 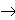 Z
Z - Объединение.
X,Y,Z
Если X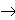 Y, X
Y, X 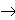 Z, то X
Z, то X 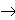 YZ
YZ - Декомпозиция.
X,Y,Z
Если X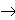 YZ, то X
YZ, то X 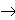 Y и X
Y и X 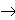 Z
Z
4.8. Нормальные формы отношений
Нормализация – это разбиение таблицы на 2 или несколько таблиц с целью улучшения её свойств при включении, добавлении или удалении данных.
Каждая таблица делится до тех пор, пока она не станет обладать некоторыми определёнными свойствами.
Свойства нормальных форм:
- Каждая нормальная форма должна обладать лучшими свойствами при включении, добавлении и удалении данных, чем предыдущая.
- Каждая следующая нормальная форма должна сохранять форму предыдущей.
Первая нормальная форма (1НФ).
При первой нормальной форме значения всех её атрибутов атомарные.
Сотрудники – отделы – проекты.
|
№сотрудника |
Зарплата |
№отдела |
№проекта |
Задание |
Ключом являются №сотрудника и №проекта
Функциональная зависимость (ФЗ):
№сотрудника ![]() зарплата (*)
зарплата (*)
№сотрудника, №проекта ![]() задание (**)
задание (**)
№сотрудника ![]() №отдела (***)
№отдела (***)
(*) и (***) – это неполные ФЗ.
Чтобы избежать аномалий, нужно данную таблицу разделить на 2 таблицы: удаляются все неполные ФЗ.
Вторая нормальная форма (2НФ).
Сотрудники – отделы
|
№сотрудника |
Зарплата |
№отдела |
Сотрудники – проекты
|
№сотрудника |
№проекта |
Задание |
ФЗ:
зарплата ![]() отдел
отдел
отдел ![]() зарплата
зарплата
сотрудник ![]() зарплата
зарплата
Третья нормальная форма (3НФ).
Сотрудники – отделы
|
№сотрудника |
№отдела |
Отдел – зарплата
|
№отдела |
Зарплата |
Отношение находится в 3НФ, когда удалены транзитивные ФЗ.
Нормальная форма Бойса-Кодда (НФБК).
|
№сотрудника |
Имя сотрудника |
№проекта |
Задание |
ФЗ:
№сотрудника ![]() имя сотрудника
имя сотрудника
№сотрудника, №проекта ![]() задание
задание
№сотрудника ![]() №проекта
№проекта
Имя сотрудника ![]() №проекта
№проекта
Исходная таблица разделяется на 2 таблицы:
|
№сотрудника |
Имя сотрудника |
|
№сотрудника |
№проекта |
Задание |
Отношение находится в НФБК, если любая нетривиальная зависимость в нём есть зависимость от ключа
№сотрудника, №проекта ![]() задание
задание
Четвёртая нормальная форма (4НФ).
Отношение находится в 4НФ, если любая многозначная зависимость в ней есть зависимость от ключа.
Достаточным условием для 4НФ является наличие в отношении не более 2 атрибутов.
|
№сотрудника |
№проекта |
Задание |
Исходная таблица разделяется на 2 таблицы:
|
№сотрудника |
№проекта |
|
№проекта |
Задание |
Пятая нормальная форма (5НФ).
Отношение находится в 5НФ тогда, когда в любой её полной декомпозиции все проекции содержат возможный ключ.
|
№сотрудника |
№отдела |
№проекта |
Ключ: №сотрудника, №отдела, №проекта
|
№сотрудника |
№отдела |
|
№сотрудника |
№проекта |
|
№отдела |
№проекта |
Общие правила нормализации:
1.T(k1,k2,F), k2 ![]() F , где Т, Т1,Т2 – это таблицы, k1, k2 – ключи.
F , где Т, Т1,Т2 – это таблицы, k1, k2 – ключи.![]()
T1(k1, k2), T2(k2, F).
3.T(k,F1,F2), F1 ![]() F2
F2![]()
T1(k, F1), T2(k, F2).

