Вторичные параметры и уравнения передачи. Реальная линия всегда обладает потерями. Однако в ряде случаев удобно считать линию идеальной, т. е. не имеющей потерь. Линия без потерь – это линия, у которой рассеяние энергии отсутствует, что имеет место при значениях первичных параметров R = 0 и G =0.

Такая идеализация оправдана для коротких по длине линий, работающих на сверхвысоких частотах (фидеров, элементов радиотехнических устройств, полосковых линий, измерительных линий, согласующих СВЧ устройств и др.), где выполняются условия R 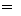wL и g 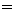wC и поэтому резистивными сопротивлением проводов и проводимостью изоляции можно пренебречь по сравнению с индуктивным сопротивлением и емкостной проводимостью линии.

Коэффициент распространения линии без потерь

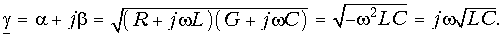
Отсюда коэффициент ослабления a = 0, а коэффициент фазы b = w 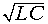линейно зависит от частоты.

Волновое сопротивление линии без потерь

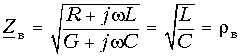
является чисто активным (резистивным).

Коэффициент фазы b связан с длиной волны электромагнитного колебания. Длиной волны l называется расстояние между двумя точками, взятыми в направлении распространения волны, фазы в которых отличаются на 2p. Следовательно, bl = 2p и l = 2p/b

Уравнения передачи линии без потерь получаются из (13.9 в), если учесть, что

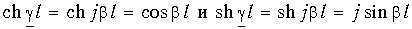
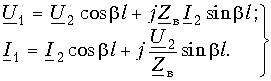
При анализе процессов, происходящих в линии без потерь, общепринято расположение той или иной точки на линии характеризовать ее удалением не от начала линии, как это делали прежде, а от конца линии (рис. 13.8). В этом случае уравнения передачи линии без потерь, выражающие комплексные действующие значения напряжения и тока в произвольной точке линии х, отсчитанной от ее конца, записываются в виде:

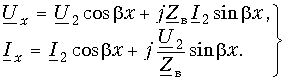
Рассмотрим различные режимы работы линии без потерь.

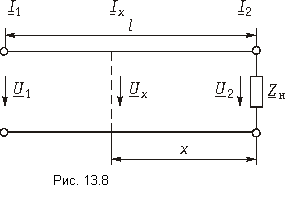
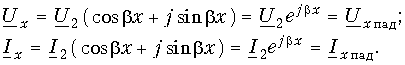
Заменяя комплексные амплитуды их модулями и фазами, т. е.

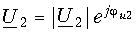
и

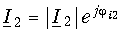
и полагая для упрощения ju2 = = ji2 = 0, перейдем к уравнениям передачи для мгновенных значений напряжений и токов. Тогда

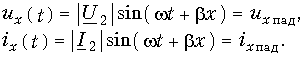
Эти уравнения описывают падающие волны, распространяющиеся в линии слева направо, т. е. от начала к концу линии (рис. 13.9, а). На направление распространения волн указывает знак «плюс» перед bx (напомним, что расстояние х отсчитывается от конца линии).

Таким образом, при согласованном включении линии без потерь в ней существуют только падающие, или бегущие, волны напряжения и тока. При этом амплитуды колебаний постоянны по всей длине линии (рис. 13.9, б). Данный режим работы линии называют также режимом бегущей волны. Сдвиг фаз между напряжением их и током ix равен нулю, поэтому энергия бегущей волны носит активный характер.

Короткое замыкание линии. При Zн = 0 напряжение в конце линии U2 = 0. Уравнения передачи (13.19) для данного режима работы линии принимают вид:

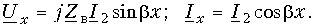
Если положить для простоты начальную фазу ji2 тока в конце линии равной нулю, то мгновенные значения напряжения и тока в любой точке линии описываются выражениями:

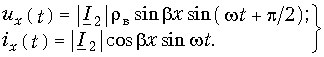
Амплитуды напряжения

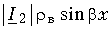
и тока

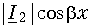
являются функциями координаты х. В линии есть точки, в которых амплитуда напряжения (тока) в любой момент времени равна нулю. Это так называемые узлы напряжения (тока). Имеются также точки, в которых амплитуда напряжения (тока) приобретает максимальное значение – пучности напряжения (тока).

Узлы напряжения и пучности тока образуются в точках, в которых bx = 0, p, 2p, ..., так как при этом sin bx = 0 и ux = 0, a cos bx = ±1 и ток ix имеет максимальную амплитуду. Пучности напряжения и узлы тока возникают в тех точках линии, где

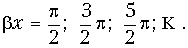
При этих значениях bх sin bх = ±1, в этом случае амплитуда напряжения ux оказывается максимальной, a cos bх = 0 и амплитуда тока ix равной нулю. Рассмотрим причины появления узлов и пуч-ностей напряжения и тока.

При КЗ линии коэффициенты отражения имеют значения

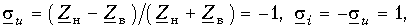
т. е. происходит полное отражение энергии, в результате чего в любой точке цепи результирующее напряжение (ток) оказывается равным сумме падающих и отраженных волн. Действительно, из уравнений в комплексной форме (13.20) следует:

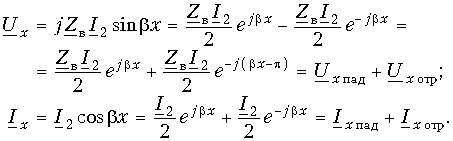
Поскольку потерь в линии нет, амплитуды падающих и отраженных волн во всех точках линии одинаковы.

Сдвиг фаз между падающей и отраженной волнами напряжения в точке х

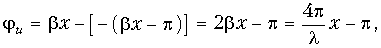
а между падающей и отраженной волнами тока

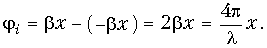
Удобно рассматривать в линии без потерь точки х, отстоящие от конца линии на расстояния, кратные четверти длины волны, т. е. кратные l/4. В конце линии (х = 0) ju = —p и ji = 0. Следовательно, падающая и отраженная волны напряжения находятся в противофазе, а падающая и отраженная волны тока – в фазе. Поэтому в конце линии наблюдается узел напряжения и пучность тока.

В промежуточных точках между узлами и пучностями фазовые соотношения отличны от 0, p 2p и т. д. В них амплитуды напряжения и тока принимают промежуточные значения между нулем и максимальным значением.

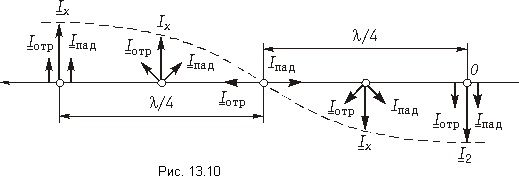
Векторная диаграмма, приведенная на рис. 13.10, иллюстрирует соотношение фаз между падающей и отраженной волнами тока в различных точках КЗ линии.

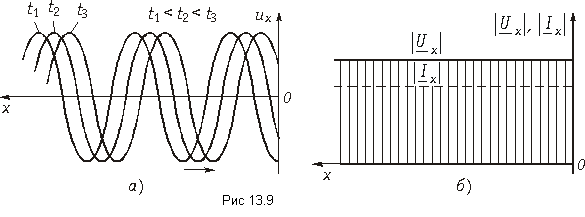
Распределение модулей комплексных амплитуд напряжения |Ux| и тока |Ix| по длине линии представлено на рис. 13.11. Расстояние между соседними узлами (пучностями) равно l/2.

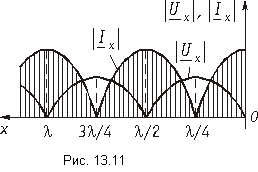
Таким образом, в КЗ линии возникают волны напряжения и тока, которые не распространяются вдоль линии, находятся на одном месте. Такие волны называются стоячими а уравнения передачи (13.20) и (13.21) – уравнениями стоячих волн. Описываемый режим работы линии получил также название режима стоячих волн

Определим входное сопротивление КЗ линии в произвольной точке х. Из (13.20) следует, что

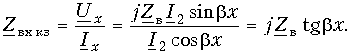
При x = 0, l/2, l, 3l/2, ... величина

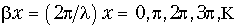
и входное сопротивление 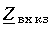= 0. При х = l/4, 3l/4, 5l/4, ... величина

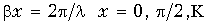
и входное сопротивление 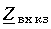= = ±j¥

На рис. 13.13 приведена зависимость

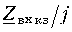
от длины линии (расстояния х от конца линии).

Меняя длину КЗ линии без потерь, можем получить входное сопротивление, имеющее индуктивный характер (в диапазоне x = = 0 ... l/4), емкостный характер (х = l/4 ... l/2), затем опять индуктивный (х = l/2 ... 3l/4) и т. д.

При длинах, кратных l/4, входное сопротивление короткозамкнутой линии без потерь эквивалентно входному сопротивлению параллельного колебательного контура, а при длинах, кратных l/2 – входному сопротивлению последовательного колебательного контура.

Учитывая, что в линиях, без потерь

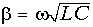
и, следовательно, частота w и длина линии l (или расстояние от конца линии х) входят в выражение 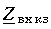симметричным образом, приходим к выводу, что частотная зависимость 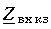аналогична зависимости от длины линии (рис. 13.14). На тех частотах, где bl кратно p/2,

,

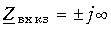а где bl кратно p, 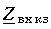= 0. При фиксированной длине КЗ линия представляет собой двухполюсник с бесконечным числом резонансов.

Размыкание линии. В режиме XX Zн = ¥ и I2 = 0. Уравнения передачи получим из (13.19):

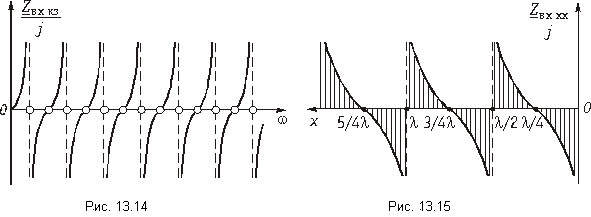
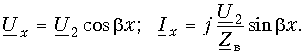
Для мгновенных значений имеем (при начальной фазе напряжения ju2 = 0):

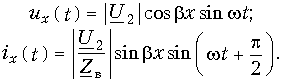
Сравнивая уравнения передачи (13.22) и (13.23) с уравнениями КЗ линии (13.20) и (13.21), видим, что полученные уравнения также являются уравнениями стоячих волн. Разница состоит в том, что узлы и пучности напряжения при XX совпадают с узлами и пучностями тока при коротком замыкании, а узлы и пучности тока разомкнутой линии – с узлами и пучностями напряжения КЗ линии. В конце разомкнутой линии образуется пучность напряжения и узел тока.

Данный режим работы линии по аналогии с предыдущим называется режимом стоячих волн. Входное сопротивление разомкнутой линии без потерь определяется из (13.22):

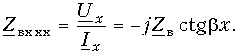
Его график, отражающий зависимость от х, дан на рис. 13.15.

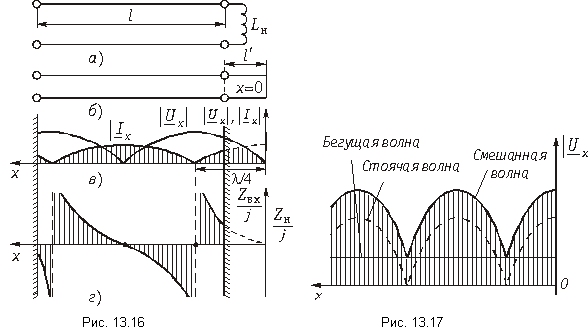
Включение линии на реактивное сопротивление. Пусть линия нагружена на индуктивность Lн (рис. 13.16, а). При заданной частоте w сопротивление нагрузки Zн = jwLн

Из рис. 13.13 видно, что отрезок закороченной линии длиной меньше l/4 имеет входное сопротивление индуктивного характера. Поэтому всегда можно подобрать такую длину отрезка l¢, при которой его входное сопротивление равнялось бы заданному сопротивлению Zн. Заменим индуктивность Lн отрезком КЗ линии (рис. 13,16, б). Эта замена позволяет применить теорию КЗ линии и сразу же построить кривые распределения напряжения и тока в линии, нагруженной на индуктивность (рис. 13.16, в). В рассматриваемой линии возникают стоячие волны. Этот режим отличается от режима КЗ замыкания тем, что ближайший узел и пучность сдвинуты от конца линии на некоторое расстояние.

В случае, когда линия нагружена на емкость Cн с сопротивлением Zн = = 1/(jwCн), можно заменить эту емкость отрезком разомкнутой линии длиной l < l/4 (см. рис. 13.15), входное сопротивление которого равняется заданному 1/(jwCн). Очевидно, и в этом случае в линии возникают стоячие волны. Предоставляем читателю возможность проанализировать данный режим работы линии самостоятельно.

Включение линии на резистивное сопротивление, не равное волновому. Положим для определенности, что сопротивление нагрузки Rн > Zв = rв, и рассмотрим распространение по линии волны напряжения.

Падающая волна не вся поглощается нагрузкой, часть ее отражается обратно в линию. Амплитуда отраженной волны меньше амплитуды падающей волны, поэтому падающую волну можно представить в виде суммы двух волн. Одна из них, равная по амплитуде отраженной волне, взаимодействуя с ней, образует стоячую волну. Отставшаяся падающая волна является бегущей. Таким образом, в линии возникает смешанная волна, состоящая из бегущей и падающей волн. Данный режим работы называется режимом смешанных волн

На рис. 13.17 показано распределение по длине линии модуля комплексной амплитуды напряжения. В линии будут отсутствовать узлы и пучности, а будут наблюдаться минимумы и максимумы амплитуды волн.

Чтобы оценить близость данного режима к режиму бегущей волны, вводят коэффициент бегущей волны

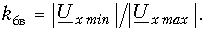
Величина kбв изменяется в пределах от 0 <= kбв <= 1. При kбв = 0 в линии имеет место стоячая волна, при kбв = 1 – бегущая волна.

Коэффициент бегущей волны можно выразить через отношение волнового сопротивления и сопротивления нагрузки. Действительно, минимальное значение амплитуды смешанной волны

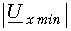
представляет собой амплитуду бегущей волны

,

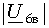т. е. той волны, которая поглощается частью сопротивления нагрузки, равной волновому сопротивлению. Поэтому

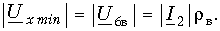
Максимальное значение амплитуды смешанной волны

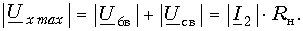
где |Ucв| – максимальная амплитуда стоячей волны. Отсюда находим

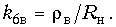
Часто используют обратную величину kcв = 1/kбв которую называют коэффициентом стоячей волны

Из общих уравнений передачи линии без потерь (13.19) рассмотрим сначала уравнение для напряжения:

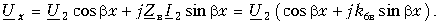
Воспользуемся подстановкой в виде тождества

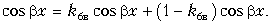
Тогда после несложных преобразований получим

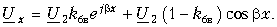
Уравнение передачи для мгновенных значений напряжения находим как обычно (полагая при этом ju2 = 0):

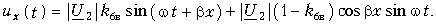
Первое слагаемое этого уравнения является бегущей волной, второе слагаемое – стоячей волной. При kбв = 0 первое слагаемое обращается в нуль и в уравнении присутствует только стоячая волна. При kбв = 1 обращается в нуль второе слагаемое и уравнение содержит только бегущую волну.

Рассматривая аналогичным образом уравнение для тока ix(t), имеем:

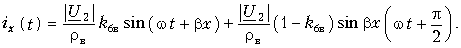
Можно сделать некоторые выводы:

• если переносимая вдоль линии энергия полностью рассеивается на ее конце (линия нагружена на резистивное сопротивление, равное волновому), то отражение энергии отсутствует и в линии существуют только бегущие волны;
• если энергия в конце линии не рассеивается (короткое замыкание, холостой ход, реактивная нагрузка), то происходит полное отражение волн, и, как следствие этого, в линии образуются только стоячие волны;
• когда переносимая вдоль линии энергия лишь частично рассеивается на ее конце (линия замкнута на резистивное сопротивление, не равное волновому), в линии одновременно присутствуют как бегущие, так и стоячие волны.