Аппроксимация функций является одним из разделов математики и широко используется в различных областях знаний. В 10.2. Графические методы расчета цепей с нелинейными резистивными двухполюсниками мы сталкивались с аппроксимацией ВАХ нелинейных элементов. И в данном случае подход к решению задачи остается прежним. Прежде всего это касается критериев близости функций. Напомним, что наиболее распространенными являются два критерия. Во-первых, это среднеквадратический критерий, когда минимизируется интеграл от квадрата модуля разности функций. Другим критерием является минимаксный критерий, когда минимизируется максимум модуля разности двух функций. Если достигается такой минимум, то говорят, что аппроксимация выполнена по Чебышеву или оптимально равномерно. Однако в решении задачи аппроксимации при синтезе цепей имеются и отличия. Во-первых, существуют ограничения на вид аппроксимирующих функций и, во-вторых, должны контролироваться УФР.

Действительно, если выполняется аппроксимация квадрата модуля передаточной функции, то в качестве аппроксимирующей необходимо выбрать дробно-рациональную функцию, которая представляет собой отношение двух четных полиномов с вещественными коэффициентами. При этом степень полинома числителя не должна превышать степени полинома знаменателя и свободный член полинома знаменателя не может равняться нулю. Таким выбором аппроксимирующей функции удовлетворяются первые два УФР квадрата модуля передаточной функции. Третье условие должно контролироваться в процессе решения аппроксимационной задачи.

Когда рассматриваются временные характеристики, то выбор аппроксимирующей функции осуществляется в соответствии с выражениями (16.7).

Методы аппроксимации. Обозначим заданную функцию (х). Как уже говорилось, это может быть: АЧХ |H(j)| или ее квадрат |H(j)|²; ФЧХ () или ее тангенс D = tg(); характеристика группового времени прохождения (ГВП) t_гр() = d ()/d ; импульсная характеристика h(t); переходная характеристика g(t) и т. д.

В качестве аппроксимирующей функции выбирают соответствующую частотную или временнyю функцию цепи F(x). Например, если задан квадрат АЧХ, т. е. (х) = |H(j)|², то функция цепи, аппроксимирующая заданную, ищется в общем случае в виде 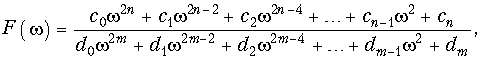где подлежат определению значения коэффициентов c₀, ..., c_n, d₀, ..., d_m.

Для заданной переходной функции (х) = g(t) аппроксимирующая функция может описываться выражением 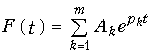, где в результате аппроксимации определяются значения коэффициентов А_k и корней характеристического уравнения p_k = a_k j_k и т. д.

Из рассмотренных примеров видно, что аппроксимирующая функция F(x) зависит от некоторых параметров цепи (в первом случае от c₀, ..., c_n, d₀, ..., d_m, во втором – от A_k и p_k и др.). Обозначим параметры цепи в общем виде буквами a₁, a₂, ..., a_N, т. е. F(x) = F(x, a₁, a₂, ..., a_N). Решением задачи аппроксимации считается нахождение наилучших значений коэффициентов a₁, a₂, ..., a_N, при которых функция F(x) будет наиболее “близка” к функции (х).

Различные аппроксимации (приближения одной функции к другой) отличаются, прежде всего, понятиями “близости” двух функций. Наиболее широкое распространение в радиотехнике и связи получили такие методы аппроксимации, как интерполяция, приближение по Тейлору, приближение по Чебышеву, среднеквадратическое приближение.

При приближении функции F(x) и (х) методом интерполяции наилучшей “близостью” этих функций считается совпадение их значений в выбранных точках – узлах интерполяции – x₁, x₂, ..., x_N, т. е.

Решение этой системы уравнений позволяет найти искомые значения коэффициентов a₁, a₂, ..., a_N.

Решение задачи аппроксимации данным методом имеет следующие недостатки:

1. Отсутствует процедура выбора точек интерполяции и первоначального порядка функции и поэтому время, необходимое для отыскания оптимального решения, зависит от квалификации и интуиции разработчика.
2. В процессе решения не контролируются УФР.

Несмотря на отмеченные недостатки, метод интерполяции применяется довольно широко на практике, например, при синтезе амплитудных корректоров.

Данный метод аппроксимации применяется довольно часто ввиду его простоты, однако он не гарантирует получения физически реализуемой функции F(x).

Приближение функций по Тейлору предполагает, что наилучшая “близость” F(x) и (х) достигается при совпадении в выбранной точке x₀ значений самих функций и их (N— 1) производных. Таким образом,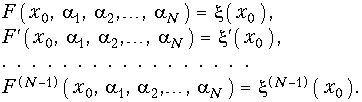

В основе этой системы уравнений лежит разложение функций F(x) и (х) в ряды Тейлора и приравнивание первых N коэффициентов соответствующих рядов. Приближение по Тейлору нашло применение, в частности, при синтезе электрических фильтров. По имени автора, впервые предложившего такой вид аппроксимации в теории фильтров, она называется аппроксимацией по Баттерворту.

Наилучшее приближение функции F(x) к (х) при аппроксимации по Чебышеву определяется из условия

Этот критерий “близости” функций следует понимать так: коэффициенты a₁, a₂, ..., a_N функции F(x) должны быть выбраны такими, чтобы самое наибольшее отклонение F(x) от (х) в любой точке х рассматриваемого диапазона сделать минимально возможным.

Задача чебышевских приближений решена аналитически для электрических фильтров.

При использовании Чебышевского критерия близости полезной является теорема Чебышева, которая формулируется следующим образом.

Теорема Чебышева. Если рациональная функция F(x, a₁, a₂, ..., a_N) с n коэффициентами аппроксимирует вещественную функцию на данном интервале по Чебышеву, то все максимумы отклонения равны между собой, а также равны величинам отклонений на границах интервала и достигаются не менее, чем в N + 1 точках, причем знаки отклонений чередуются.

Эта теорема отвечает на вопрос: данная аппроксимация выполнена оптимально или нет.

При среднеквадратическом приближении наилучшая “близость” двух функций достигается при выполнении условия 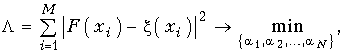т.е. при таких значениях коэффициентов a₁, a₂, ..., a_N, при которых сумма квадратов отклонений F(x) от (х) в точках x₁, x₂, ..., x_M (M > N) является минимально возможной.

Минимизация достигается путем составления и решения системы алгебраических уравнений:

Отметим, что заданная и аппроксимирующие функции могут быть не только вещественными, но и комплексными, что позволяет одновременно аппроксимировать как АЧХ, так и ФЧХ.

При решении задач среднеквадратических приближений разработано большое количество численных методов, предназначенных для использования их на ЭВМ.

Заметим, что не существует четких рекомендаций по применению того или иного метода аппроксимации. Зачастую выбор метода зависит от сложности решения задачи аппроксимации (аналитического или численного), от конкретного применения синтезированной цепи и т. п.