В реальных условиях при передаче сообщений сигнал в точке приема заранее неизвестен и поэтому не может быть описан определенной функцией времени. То же самое можно сказать и о помехах, появление которых ,в канале может быть обусловлено самыми различными и чаще всего неизвестными для нас причинами.

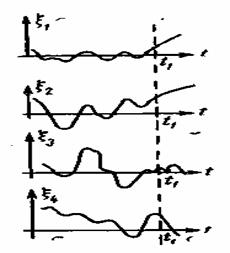
Рис. 2.2. Реализации случайного процесса

Таким образом, реальные сигналы и помехи представляют собой случайные процессы. Случайный процесс описывается случайной функцией, значения которой при любом значении аргумента являются случайными величинами. Аргументом функции может быть величина любой физической природы. Для электрических сигналов такой величиной обычно является время. При неизменных условиях опыта случайный процесс ξ(t) может принимать ту или иную конкретную форму ξ(t) (рис. 2.2). Эти возможные формы случайного процесса называются его реализациями. Совокупность всех возможных реализаций {ξ(t)} случайного процесса ξ(t) называется ансамблем. Реализации ξ(t) уже являются не случайными, а детерминированными функциями. Однако предсказать, какова будет реализация процесса в каждом конкретном опыте, невозможно.

Если рассматривать не каждую реализацию в отдельности, а совокупность их большого числа, то можно определить вероятностные характеристики случайного процесса. Такими характеристиками являются законы распределения, которые могут быть получены теоретически или на основе экспериментальных данных.

Пусть ξ(t) есть случайный процесс. В некоторый фиксированный момент времени t различные реализации процесса будут иметь различные значения (рис. 2.2). Значение является случайной величиной.

Одномерная функция распределения или интегральный закон распределения определяется как вероятность того, что случайная величина не превысит некоторого значения x.

F(x,t)= (2.5)

Частная производная

(2.6)

называется одномерной плотностью вероятности случайного процесса {ξ(t)} для t=t.

Двумерным интегральным законом распределения случайного процесса {ξ(t)} называется вероятность того, что в момент t функция {ξ(t)} не превысит некоторого значения x, а в момент — значения х2, т. е.

= (2.7)

Двумерная плотность вероятности определяется как частная производная (если она существует) второго порядка

(2.8)

Произведение выражает вероятность того, что в момент времени t функция ξ(t) находится в интервале между xи x+dx, а в момент времени — в интервале между х2и х2+dх2. Аналогично определяются трехмерный, четырехмерный, и т. д. законы распределения.

Наиболее полной характеристикой случайного процесса является n-мерный закон распределения, т. е. распределение значения ξ(t) для п произвольно выбранных моментов времени. Функция

(2.9)

называется n-мерным интегральным законом распределения, а частотная производная

(2.10)

называется n- мерной плотностью вероятности.

Случайный процесс задай, если его n-мерное распределение известно для любого числа n произвольно выбранных моментов времени .Если значения случайной функции l(t) при любых значениях t независимы, то

(2.11)

Отсюда следует, что исчерпывающей характеристикой случайной функции с независимыми значениями является ее одномерный закон распределения.

Законы распределения являются достаточно полными характеристиками случайного процесса. Однако они сложны и требуют для своего определения обработки большого экспериментального материала. Кроме того, такое подробное описание процесса не всегда бывает нужным. Для решения многих практических задач достаточно знать более простые (хотя и менее полные) характеристики случайного процесса. Такими характеристиками являются средние значения и функция корреляции случайного процесса.

(2.21)

В дальнейшем, говоря о стационарных процессах, мы будем иметь в виду стационарность в широком смысле.

Для стационарных процессов в большинстве практически важных случаев справедлива эргодическая теорема, согласно которой усреднение по ансамблю можно заменить усреднением по времени, т. е. с вероятностью, сколь угодно близкой к единице, можно считать:

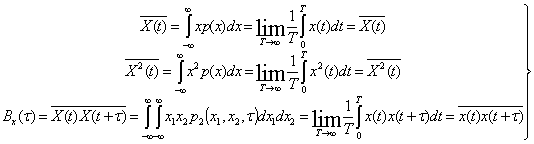(2.22)

Свойство эргодичности имеет большое практическое значение. Оно позволяет при исследовании статистических свойств процесса рассматривать не множество его реализаций, а всего лишь одну реализацию достаточно большой продолжительности. Например, при изучении свойств шума на выходе усилителя не нужно иметь большое число одинаковых усилителей, дающих различные реализации шума; достаточно взять один усилитель и исследовать шум на его выходе в течение длительного промежутка времени.

Важнейшей характеристикой эргодического процесса является его корреляционная функция. Поясним физический смысл этой функции. Пусть x(t) есть электрическое напряжение на выходе приемника. Если в момент t значение x(t) велико, то мало вероятно, что в момент t+τ, где τ — малая величина, оно станет очень малым. Если же взять τ достаточно большим, то величина x(t+τ) может быть уже какой угодно. Другими славами, между x(t) и x(t+τ) имеется зависимость, которая ослабевает с увеличением τ. Мерой этой зависимости может быть среднеквадратическое отклонение x(t) от x(t+τ),т. е.

Отсюда следует, что среднеквадратическое отклонение полностью определяется корреляционной функцией, которая указывает, насколько в среднем связаны друг с другом два значения эргодического процесса, разделенные интервалом времени τ.

Основными свойствами корреляционной функции являются следующие:

— автокорреляционная функция эргодического процесса является функцией четной, т. е. Bx(τ)= Bx(-τ)

— из определения (2.22) ясно, что Вх(0)==σ, т. е. значение корреляционной функции эргодического процесса при т=0 совпадает co средней мощностью этого процесса;

— любое значение корреляционной функции не может превышать значения этой функции при τ=0, т. е. Это вытекает из неравенства

я корреляционная функция не превосходит по модулю единицы: ρ(τ)1;

— если автокорреляционная функция процесса удовлетворяет условиям:

ВХ(0)0 при τ=0

Bx(τ)= 0 при |τ|>0,

то это означает, что между значениями x(t) и x(t+ τ) не существует связи. Taкиe процессы называют чисто случайными;

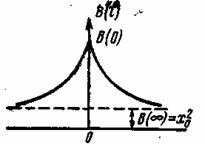
Рис. 2.3. График корреляционной функции эргодического процесса

— если эргодический процесс не содержит детерминированной составляющей, то его корреляционная функция неограниченно убывает с увеличением τ, т. е. зависимость между значениями x(t) и х(t+ τ) ослабевает и в пределе (при τ) они становятся независимыми. Наличие постоянной (детерминированной) составляющей в процессе x(t)=ξ(t)+x приводит к тому, что

На рас. 2.3 приведена типичная кривая корреляционной функции эргодического процесса, иллюстрирующая перечисленные свойства этой функции;

—функция автокорреляции периодического процесса есть периодическая функция с периодом этого процесса. Пусть имеется периодический процесс x(t)=

Тогда, в силу периодичности x(t), беря среднее за период, имеем

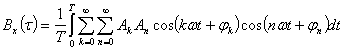
Ввиду того что интегралы от произведения косинусов при nk равны нулю, а n=k0 при эти интегралы равны — получаем

(2.23)

Заметим, что корреляционная функция не зависит от фазовых углов гармоник исходного периодического процесса.

Для случайного процесса, не содержащего детерминированных составляющих, можно указать такой интервал Δτ, что при τ>Δτ взаимная связь между значениями x(t) и x(t+ τ) будет несущественной (их можно считать некоррелированными). Этот интервал называется интервалом корреляций. Его обычно определяют шириной основания прямоугольника единичной высоты, площадь которого равна площади, ограниченной кривой коэффициента корреляции и осью абсцисс:

(2.24)

В ряде случаев случайный процесс представляет собой дискретную последовательность элементов (i=l, 2, . . ., п). Статистические свойства такой последовательности описываются вероятностями появления отдельных элементов p(), P(), . . ., Р(ап), причем , т. е. элементы последовательности образуют полную совокупность. Вероятности P() определяются из опыта или задаются заранее и поэтому называются априорными (доопытными) .

Для многих реальных дискретных сигналов вероятность выбора отдельных элементов последовательности зависит от предшествующих элементов. Вероятность сложного события, состоящего в последовательном выборе двух элементов и , определяется совместной вероятностью

(2.25)

где — условная вероятность, т. е. вероятность появления символа за символом . Из выражения (2.25) следует известная в теории вероятностей формула Байеса

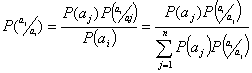(2.26)

Если вероятность появления отдельных элементов зависит от конечного числа элементов, предшествующих данному, то такая последовательность называется однородной сложной цепью Маркова. В частном случае, когда вероятность появления элемента зависит только от предшествующего элемента, цепь Маркова называется простой. Среди возможных цепей Маркова в теории передачи сигналов имеют большое значение эргодические цепи. Эргодичность означает статистическую однородность. Если процесс эргодический, то каждая последовательность, создаваемая процессом, имеет одинаковые статистические свойства. Если элементы в, и независимы, то P(,)=P()P() и P(/) = P().