Нелинейный четырехполюсник, предназначенный для ограничения мгновенных напряжений сигнала, называется ограничителем.

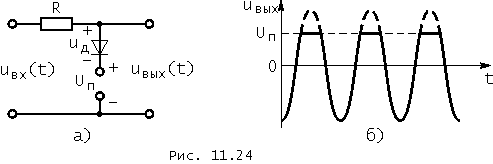
Схема простейшего ограничителя с ограничением сверху приведена на рис. 11.24, а. В ограничитель входят линейный резистор с сопротивлением R, выпрямительный диод и генератор постоянного напряжения с задающим пороговым напряжением U_п. На первом этапе анализа процессов в рассматриваемом ограничителе будем считать, во-первых, что диод идеален, т. е. его сопротивление или бесконечно велико, если u_д < 0, или равно нулю, если u_д > 0, и во-вторых, что внутреннее сопротивление генератора постоянного напряжения равно нулю.

Если при указанных предположениях напряжение на зажимах диода будет отрицательным, т. е. когда u_вх(t) < U_п, диод будет "закрыт" и напряжение на выходе ограничителя будет равно напряжению на его входе, т. е. u_вых(t) = u_вх(t). Если же u_вх(t) > U_п, диод "открывается", его сопротивление становится равным нулю. Тем самым источник постоянного напряжения подключается к выходу ограничителя и напряжение на выходе ограничителя будет равно задающему напряжению источника U_п на протяжении всего времени пока u_вх > U_п. Итак:

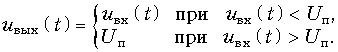
Соответствующая графическая иллюстрация приведена на рис. 10.24, б для воздействия в виде гармонического колебания . Штриховой линией на рисунке показаны "отсеченные" ограничителем участки входного колебания.

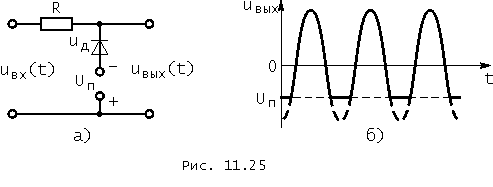
На рис. 11.25, а изображена схема ограничителя с ограничением снизу. Аналогичные рассуждения показывают, что у такого ограничителя при тех же, что и выше, допущениях:

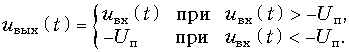
График напряжения на выходе ограничителя с ограничением снизу для того же, гармонического, воздействия изображен на рис. 10.25, б.

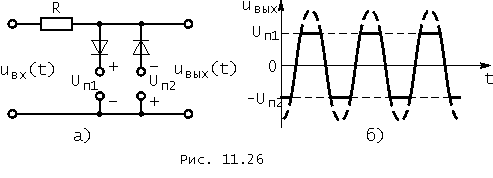
Наконец, на рис. 11.26, а приведена схема ограничителя с двухсторонним ограничением, у которого для принятых допущений

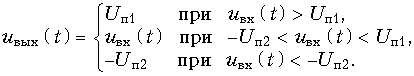
Обычно ограничители с двухсторонним ограничением имеют как симметричные, так и асимметричные пределы ограничений.

Напряжение на выходе ограничителя с симметричными пределами ограничения, если к его входу подается гармоническое напряжение , по форме близко к периодической последовательности импульсов трапециедальной формы и чередующейся полярности (см. рис. 11.2). Форма импульсов приближается к прямоугольной по мере усиления неравенства U_m> U_п1 = U_п2.

Если рассматриваемую периодическую последовательность импульсов подвести к устройству, моделирующему операцию дифференцирования, то напряжение на его выходе будет представлять собой периодическую последовательность коротких импульсов чередующейся полярности. Форма каждого отдельного импульса близка к прямоугольной; его длительность тем меньше, а высота тем больше, чем больше амплитуда гармонического колебания превышает порог ограничения.

В заключение заметим, что задачу анализа колебаний в ограничителе можно решать с учетом реальных характеристик диодов и конечного внутреннего сопротивления генераторов. При этом качественно картина процессов в ограничителе практически сохранится без изменений по сравнению с рассмотренной выше.