2.1. Формулировка задачи и правила оценки
2.4. Комплексная огибающая радиосигнала
2.5. Автокорреляционная функция и отклик согласованного фильтра
2.6. Оценка запаздывания радиосигнала
2.1. Формулировка задачи и правила оценки
В большинстве систем необходимая информация содержится в текущем значении некоторого сигнального параметра (например, амплитуды, частоты, начальной фазы, запаздывания и др.) и для ее извлечения наблюдатель должен измерить или оценить соответствующий параметр. Предположим, что наблюдение ![]() наряду с шумом содержит сигнал
наряду с шумом содержит сигнал ![]() , являющийся детерминированным, за исключением неизвестного значения постоянного параметра
, являющийся детерминированным, за исключением неизвестного значения постоянного параметра ![]() . Наблюдатель, основываясь на анализе
. Наблюдатель, основываясь на анализе ![]() , должен принять решение о том, какое конкретное значение из диапазона возможных принял параметр сигнала
, должен принять решение о том, какое конкретное значение из диапазона возможных принял параметр сигнала ![]() . Естественным является вопрос: какое правило решения является оптимальным, т.е. гарантирующим наименьший ущерб от отклонений
. Естественным является вопрос: какое правило решения является оптимальным, т.е. гарантирующим наименьший ущерб от отклонений ![]() от
от ![]() .
.
Простейший подход к этой проблеме основывается на понимании того факта, что задача оценки или измерения неизвестного параметра не является чем-то принципиально новым по отношению к задаче различения ![]() сигналов, отличающихся друг от друга только значением параметра
сигналов, отличающихся друг от друга только значением параметра ![]() :
:
![]()
Для того, чтобы охватить подобной постановкой и случай непрерывного параметра ![]() , требуется лишь устремить число его возможных значений
, требуется лишь устремить число его возможных значений ![]() , т.е. различаемых сигналов, к бесконечности (вплоть до несчетной). Учитывая это, не трудно увидеть, что оптимальное оценивание параметра l заключается в минимизации расстояния
, т.е. различаемых сигналов, к бесконечности (вплоть до несчетной). Учитывая это, не трудно увидеть, что оптимальное оценивание параметра l заключается в минимизации расстояния ![]() между наблюдением
между наблюдением ![]() и сигналом
и сигналом ![]() , определяемого как
, определяемого как
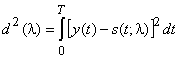 .
.
Это правило формирует максимально правдоподобную оценку ![]() , находя такое значение
, находя такое значение ![]() , при котором сигнал
, при котором сигнал ![]() наиболее близок к наблюдению
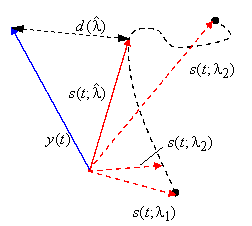
наиболее близок к наблюдению ![]() в смысле евклидова расстояния (см. рисунок). В геометрической интерпретации сигнал
в смысле евклидова расстояния (см. рисунок). В геометрической интерпретации сигнал ![]() можно отождествить с вектором
можно отождествить с вектором ![]() , который перемещается в пространстве по некоторой траектории с изменением параметра
, который перемещается в пространстве по некоторой траектории с изменением параметра ![]() , и в качестве оценки выбирается такое значение
, и в качестве оценки выбирается такое значение ![]() , которое отвечает точке этой траектории, ближайшей к вектору наблюдения
, которое отвечает точке этой траектории, ближайшей к вектору наблюдения ![]() :
:
![]() .
.
После раскрытия скобок в выражении для квадрата расстояния получаем
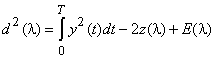 ,
,
где
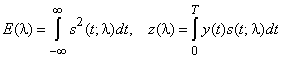
соответственно энергия сигнала и корреляция между наблюдением ![]() и сигналом
и сигналом ![]() как функции измеряемого параметра l. Из последнего соотношения видно, что при известном наблюдении
как функции измеряемого параметра l. Из последнего соотношения видно, что при известном наблюдении ![]() первое слагаемое в выражении для
первое слагаемое в выражении для ![]() фиксировано, и нахождение оптимальной оценки l может быть осуществлено (как и ранее при различении M сигналов) путем максимизации разности
фиксировано, и нахождение оптимальной оценки l может быть осуществлено (как и ранее при различении M сигналов) путем максимизации разности ![]() .
.
Общепринято подразделять параметры сигнала на два класса: если энергия сигнала зависит от параметра l, то последний называется энергетическим, в противном случае l является неэнергетическим параметром. Во втором случае единственным фактором, определяющим зависимость усредненного квадрата расстояния от ![]() , является корреляция
, является корреляция ![]() , и оптимальной оценкой служит значение l, максимизирующее
, и оптимальной оценкой служит значение l, максимизирующее ![]() :
:
![]() .
.
В свете физической трактовки корреляции последнее правило оценки имеет весьма прозрачную интерпретацию: оптимальная оценка неэнергетического параметра ![]() отвечает такому значению
отвечает такому значению ![]() , при котором сигнал
, при котором сигнал ![]() имеет максимальное сходство с наблюдаемым колебанием
имеет максимальное сходство с наблюдаемым колебанием ![]() .
.
Продолжая опираться на аналогию между распознаванием M сигналов одинаковой энергии и измерением неэнергетического параметра, можно предположить, что достоверность измерения будет зависеть не только от соотношения уровней сигнала и шума (ОСШ), но и от подобия сигнальных копий ![]() при различных значениях l. Действительно, для непрерывного параметра l гораздо уместнее характеризовать качество измерения с позиции точности, т.е. дисперсией оценки, а не вероятностью ошибочного решения. В свете сказанного коэффициент корреляции между рассогласованными по l сигнальными копиями
при различных значениях l. Действительно, для непрерывного параметра l гораздо уместнее характеризовать качество измерения с позиции точности, т.е. дисперсией оценки, а не вероятностью ошибочного решения. В свете сказанного коэффициент корреляции между рассогласованными по l сигнальными копиями ![]() и
и ![]()
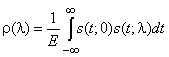 ,
,
характеризующий степень подобия, критически влияет на точность измерения неэнергетического параметра l.
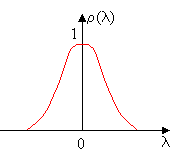
Коэффициент корреляции является четной функцией, достигающей максимума ![]() при
при ![]() (см. рисунок справа). Чем быстрее копия сигнала, расстроенная по
(см. рисунок справа). Чем быстрее копия сигнала, расстроенная по ![]() , теряет свое сходство с исходной версией, тем больше острота
, теряет свое сходство с исходной версией, тем больше острота ![]() в нулевой точке, а значит, выше точность измерения l. Из курса математического анализа известно, что кривизна или острота функции в рассматриваемой точке определяется второй производной и для выпуклой кривой имеет отрицательный знак. На основании этого следующее выражение для дисперсии оптимальной оценки неэнергетического параметра
в нулевой точке, а значит, выше точность измерения l. Из курса математического анализа известно, что кривизна или острота функции в рассматриваемой точке определяется второй производной и для выпуклой кривой имеет отрицательный знак. На основании этого следующее выражение для дисперсии оптимальной оценки неэнергетического параметра
![]()
является вполне ожидаемым и легко объяснимым. Последний факт подсказывает общее направление синтеза сигналов в задачах оценки неэнергетического параметра ![]() . Для достижения нужной точности не за счет «грубой силы», т.е. простого увеличения энергии, следует синтезировать сигналы, у которых коэффициент корреляции
. Для достижения нужной точности не за счет «грубой силы», т.е. простого увеличения энергии, следует синтезировать сигналы, у которых коэффициент корреляции ![]() как функция
как функция ![]() подобен «острому» импульсу.
подобен «острому» импульсу.
2.2. Оценка амплитуды сигнала
Предположим, что информация содержится в амплитуде сигнала. Данная ситуация характерна для многих приложений: от телевизионного вещания до сотовой связи и цифровых линий передачи данных. Сформулируем ее как задачу измерения неизвестной амплитуды ![]() , постоянной на интервале наблюдения
, постоянной на интервале наблюдения ![]() . При этом принятый полезный сигнала может быть представлен моделью
. При этом принятый полезный сигнала может быть представлен моделью
![]() ,
,
где ![]() – детерминированный эталонный сигнал, амплитуда и энергия которого по определению полагаются равными единице и E соответственно. Тогда энергия
– детерминированный эталонный сигнал, амплитуда и энергия которого по определению полагаются равными единице и E соответственно. Тогда энергия ![]() сигнала с амплитудой
сигнала с амплитудой ![]() найдется как
найдется как
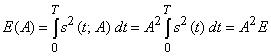 ,
,
что определяет квадрат расстояния между ![]() и
и ![]() в виде
в виде
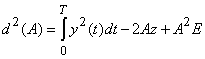 , где
, где 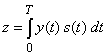 –
–
корреляция наблюдения ![]() с эталонным сигналом
с эталонным сигналом ![]() .
.
Максимизация по ![]() разности
разности ![]() дает следующее оптимальное правило оценивания амплитуды
дает следующее оптимальное правило оценивания амплитуды ![]() , которое сразу же приводит к выражению для дисперсии оценки амплитуды
, которое сразу же приводит к выражению для дисперсии оценки амплитуды
![]() .
.
Последняя формула показывает, что точность оценки зависит исключительно от энергии E эталонного сигнала.
Никакое усложнение закона модуляции при неизменной энергии сигнала не в состоянии повысить точность измерения. Следовательно, рассмотренная классическая задача приема не содержит предпосылок к привлечению широкополосной технологии.
2.3. Оценка фазы сигнала
Обратимся теперь к ситуации, в которой носителем полезной информации выступает начальная фаза сигнала ![]() :
:
![]() ,
,
где ![]() – огибающая сигнала (закон амплитудной модуляции), а
– огибающая сигнала (закон амплитудной модуляции), а ![]() – несущая частота. Данный случай типичен для когерентных локационных и навигационных приемников, демодуляторов систем мобильной радиосвязи 2-го и 3-го поколений и многих других приложений.
– несущая частота. Данный случай типичен для когерентных локационных и навигационных приемников, демодуляторов систем мобильной радиосвязи 2-го и 3-го поколений и многих других приложений.
Поскольку энергия сигнала не зависит от j ![]() , то фаза является неэнергетическим параметром, и точность измерения определяется только отношением сигнал-шум (т.е. энергией сигнала E) и коэффициентом корреляции между двумя копиями сигнала, сдвинутыми друг относительно друга по фазе j:
, то фаза является неэнергетическим параметром, и точность измерения определяется только отношением сигнал-шум (т.е. энергией сигнала E) и коэффициентом корреляции между двумя копиями сигнала, сдвинутыми друг относительно друга по фазе j:
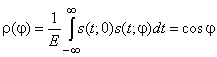 ,
,
где учтено, что ![]() есть по определению косинус угла между двумя сдвинутыми по фазе на угол
есть по определению косинус угла между двумя сдвинутыми по фазе на угол ![]() копиями сигнала, т.е. двумя векторами, разделенными углом
копиями сигнала, т.е. двумя векторами, разделенными углом ![]() .
.
Вторая производная ![]() по j в нулевой точке есть
по j в нулевой точке есть ![]() , что после подстановки в выражение для оценки дисперсии неэнергетического параметра дает
, что после подстановки в выражение для оценки дисперсии неэнергетического параметра дает
![]() .
.
Вновь, как и в случае измерения амплитуды, точность оценки фазы зависит только от отношения сигнал-шум. Таким образом, и эта классическая задача приема нейтральна к закону модуляции при неизменности энергии сигнала и, следовательно, никак не стимулирует к применению широкополосных сигналов.
Содержание следующих двух параграфов находится несколько в стороне от основной линии, однако они необходимы для напоминания некоторых важных положений основ теории сигналов.
2.4. Комплексная огибающая радиосигнала
Любой радиосигнал может быть представлен как результат модуляции амплитуды и фазы непрерывного косинусоидального колебания (несущей). Спектр радиосигнала располагается в окрестностях несущей частоты ![]() (см. рисунок).
(см. рисунок).
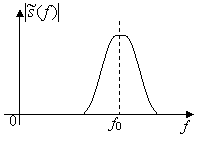
В соответствие с подобной трактовкой любой радиосигнал может быть формализован следующей моделью
![]() ,
,
в которой ![]() – действительная огибающая сигнала (закон амплитудной модуляции),
– действительная огибающая сигнала (закон амплитудной модуляции), ![]() – закон фазовой (угловой) модуляции. Анализ радиосигналов значительно упрощается при введении в обращение комплекснозначной функции времени
– закон фазовой (угловой) модуляции. Анализ радиосигналов значительно упрощается при введении в обращение комплекснозначной функции времени
![]() ,
,
где комплексная огибающая
![]()
объединяет в себе законы как амплитудной, так и угловой модуляции сигнала. Если рассматриваются несколько сигналов одной и той несущей частоты, их отличие состоит только в законах модуляции, и, следовательно, в комплексных огибающих содержится их исчерпывающее описание. Ярчайшим примером продуктивности этого понятия служит комплексный интеграл свертки для комплексной огибающей отклика полосового фильтра на входной радиосигнал
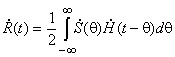 ,
,
где вещественная импульсная характеристика ![]() фильтра заменяется на ее комплексную огибающую аналогично процедуре, осуществляемой с входным радиосигналом
фильтра заменяется на ее комплексную огибающую аналогично процедуре, осуществляемой с входным радиосигналом
![]() .
.
Применение комплексного интеграла свертки позволяет за один шаг определить законы амплитудной и фазовой модуляции на выходе фильтра, представляя реакцию фильтра ![]() на входной сигнал следующим образом
на входной сигнал следующим образом
![]() .
.
2.5. Автокорреляционная функция и отклик согласованного фильтра
Теория систем с расширенным спектром в значительной степени базируется на понятии автокорреляционной функции (АКФ) сигнала, являющейся скалярным произведением двух копий одного и того же сигнала, сдвинутых по времени относительно друг друга на ![]() секунд:
секунд:
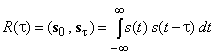 ,
,
характеризуя степень сходства или подобия между ними. Умножение на ![]() приводит к нормированной версии АКФ
приводит к нормированной версии АКФ
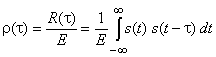 ,
,
являющейся попросту коэффициентом корреляции сдвинутых во времени копий сигнала ![]() и
и ![]() , или в геометрической интерпретации косинусом угла между ними.
, или в геометрической интерпретации косинусом угла между ними.
В соответствие с общими свойствами коэффициента корреляции АКФ – четная функция ![]() , имеющая максимум в нуле
, имеющая максимум в нуле
![]() .
.
Для любого радиосигнала АКФ может быть представлена как
![]() ,
,
где
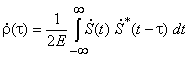
коэффициент корреляции двух сдвинутых по времени копий комплексной огибающей ![]() сигнала. Как можно заметить, АКФ
сигнала. Как можно заметить, АКФ ![]() радиосигнала
радиосигнала ![]() может считаться радиосигналом, комплексная огибающая которого определяется АКФ
может считаться радиосигналом, комплексная огибающая которого определяется АКФ ![]() комплексной огибающей сигнала
комплексной огибающей сигнала ![]() . В частности, действительная огибающая
. В частности, действительная огибающая ![]() АКФ
АКФ ![]() является модулем
является модулем ![]() :
: ![]()
Технически любая АКФ может быть получена как выходной сигнал коррелятора, причем вычисления во всем диапазоне значений ![]() выполняются раздельно по точкам. Альтернативной структурой является согласованный фильтр (СФ), вычисляющий и воспроизводящий АКФ как выходной сигнал в реальном времени. Для фиксированного сигнала СФ максимизирует среди всех линейных систем выходное отношение сигнал-шум. Если приложить сигнал
выполняются раздельно по точкам. Альтернативной структурой является согласованный фильтр (СФ), вычисляющий и воспроизводящий АКФ как выходной сигнал в реальном времени. Для фиксированного сигнала СФ максимизирует среди всех линейных систем выходное отношение сигнал-шум. Если приложить сигнал ![]() ко входу согласованного с ним фильтра, то реакция фильтра
ко входу согласованного с ним фильтра, то реакция фильтра ![]() воспроизведет АКФ
воспроизведет АКФ ![]() в реальном времени с задержкой, равной длительности сигнала T:
в реальном времени с задержкой, равной длительности сигнала T:
![]() .
.
Пример 2.5.1. Прямоугольный видеоимпульс ![]() длительности
длительности ![]() (см. рисунок а) обладает треугольной АКФ
(см. рисунок а) обладает треугольной АКФ ![]() длительности
длительности ![]() с максимумом в нулевой точке (рисунок b, пунктирная линия). Реакция на него согласованного фильтра
с максимумом в нулевой точке (рисунок b, пунктирная линия). Реакция на него согласованного фильтра ![]() представляет собой копию АКФ с запаздыванием, равным длительности сигнала
представляет собой копию АКФ с запаздыванием, равным длительности сигнала ![]() , так что максимальное напряжение на выходе фильтра наблюдается в момент окончания входного сигнала (рисунок b, сплошная линия). Для радиоимпульса
, так что максимальное напряжение на выходе фильтра наблюдается в момент окончания входного сигнала (рисунок b, сплошная линия). Для радиоимпульса ![]() с прямоугольной огибающей АКФ оказывается треугольным радиоимпульсом (рисунок с, пунктирная линия), а сигнал на выходе согласованного фильтра – запаздывающей на
с прямоугольной огибающей АКФ оказывается треугольным радиоимпульсом (рисунок с, пунктирная линия), а сигнал на выходе согласованного фильтра – запаздывающей на ![]() копией последнего (рисунок с, сплошная линия).
копией последнего (рисунок с, сплошная линия).
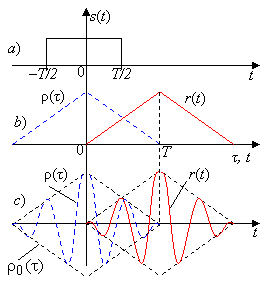
Максимум отклика фильтра, согласованного с сигналом, всегда приходится на момент окончания сигнала (по крайней мере, не ранее), поскольку этот фильтр должен обработать весь сигнал целиком. Поучительно также отметить, что для радиосигнала моменты максимумов огибающей и высокочастотного заполнения на выходе согласованного фильтра всегда совпадают, поскольку любая АКФ имеет максимум в начале координат.
2.6. Оценка запаздывания радиосигнала
Рассматриваемая задача является одной из наиболее часто встречающихся в радиотехнических приложениях. Она типична для телевидения (каналы синхронизации), цифровых систем мобильной радиосвязи (пилотные каналы, тактовая синхронизация), радиолокации (измерение дальности до цели), навигации космического и наземного базирования (измерение расстояния до маяков) и т.п. Дополнительное обращение к основам теории сигналов в двух предыдущих параграфах было обусловлено стремлением облегчить знакомство с задачей измерения временного запаздывания.
Предположим, что радиосигнал
![]() ,
,
распространяясь по каналу, приобретает неизвестные запаздывание ![]() и начальную фазу
и начальную фазу ![]() , т.е. принимает вид
, т.е. принимает вид
![]() .
.
Во многих ситуациях фаза ![]() случайна и равномерно распределена на интервале
случайна и равномерно распределена на интервале ![]() . Включим фазовый набег, обусловленный запаздыванием
. Включим фазовый набег, обусловленный запаздыванием ![]() в полную начальную фазу
в полную начальную фазу ![]() . Последняя, оставаясь случайной и равномерно распределенной на интервале
. Последняя, оставаясь случайной и равномерно распределенной на интервале ![]() , вновь независима с
, вновь независима с ![]() , т.е. не содержит информации об измеряемом временном сдвиге, вследствие деструктивного вклада
, т.е. не содержит информации об измеряемом временном сдвиге, вследствие деструктивного вклада ![]() . Тогда принятый сигнал может быть представлен как
. Тогда принятый сигнал может быть представлен как
![]() ,
,
где запаздывание ![]() является неизвестным полезным параметром, подлежащим измерению, а
является неизвестным полезным параметром, подлежащим измерению, а ![]() – бесполезная начальная фаза, неопределенность которой лишь потенциально затрудняет оценку
– бесполезная начальная фаза, неопределенность которой лишь потенциально затрудняет оценку ![]() . Из последнего соотношения видно, что интересующая нас информация затрагивает только комплексную огибающую сигнала
. Из последнего соотношения видно, что интересующая нас информация затрагивает только комплексную огибающую сигнала ![]() . Поскольку наблюдаемое колебание
. Поскольку наблюдаемое колебание ![]() является таким же радиосигналов сигналом, как и
является таким же радиосигналов сигналом, как и ![]() , то его можно записать в виде
, то его можно записать в виде
![]() ,
,
где ![]() – комплексная огибающая наблюдения
– комплексная огибающая наблюдения ![]() .
.
Тогда можно заметить, что в данных условиях минимизация Евклидова расстояния, направленная на оценку величины t, может быть упрощена заменой некогерентных сигналов их детерминированными законами модуляции, т.е. комплексными огибающими:
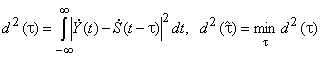
Учитывая, что запаздывание – неэнергетический параметр, минимизация этого расстояния эквивалентна максимизации корреляции упомянутых комплексных огибающих
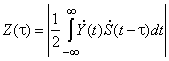 .
.
Точность измерения t регулируется коэффициентом корреляции рассогласованных во времени копий комплексной огибающей сигнала, который показывает степень их сходства как функции рассогласования по времени t:
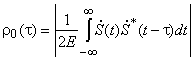 .
.
Этот коэффициент корреляции представляет собой модуль АКФ комплексной огибающей сигнала, который определяет форму АКФ всего сигнала ![]() . В сопоставлении с двумя ранее рассмотренным измерительными задачами ситуация выглядит достаточно новой. Имеется реальный ресурс повышения точности вне варианта «грубой силы», т.е. простого увеличения энергии. В рассматриваемом случае оценка запаздывания сигнала t может быть выполнена более точно без привлечения дополнительной энергии, а только за счет остроты автокорреляционной функции сигнала. Наряду со второй производной
. В сопоставлении с двумя ранее рассмотренным измерительными задачами ситуация выглядит достаточно новой. Имеется реальный ресурс повышения точности вне варианта «грубой силы», т.е. простого увеличения энергии. В рассматриваемом случае оценка запаздывания сигнала t может быть выполнена более точно без привлечения дополнительной энергии, а только за счет остроты автокорреляционной функции сигнала. Наряду со второй производной ![]() в качестве индикатора остроты АКФ может служить интервал (время) корреляции сигнала
в качестве индикатора остроты АКФ может служить интервал (время) корреляции сигнала ![]() , характеризующий ширину АКФ сигнала вдоль оси t. Чем меньше интервал корреляции
, характеризующий ширину АКФ сигнала вдоль оси t. Чем меньше интервал корреляции ![]() , тем острее или короче АКФ сигнала.
, тем острее или короче АКФ сигнала.
Согласно известным свойствам преобразования Фурье, интервал корреляции обратно пропорционален полосе W, т.е.![]() . Другими словами чем уже АКФ, тем шире спектр сигнала и наоборот. Прямым следствием этого оказывается возможность повышения точности измерения времени не только за счет энергии, но и путем использования сигналов с широким спектром:
. Другими словами чем уже АКФ, тем шире спектр сигнала и наоборот. Прямым следствием этого оказывается возможность повышения точности измерения времени не только за счет энергии, но и путем использования сигналов с широким спектром:
![]() ,
,
где константа a, как правило, имеет порядок единицы, а ее точное значение зависит от формы сигнала и способа определения ширины полосы.
Таким образом, использование сигнала с широкой полосой ![]() , или, что эквивалентно, узкой АКФ (малым временем корреляции
, или, что эквивалентно, узкой АКФ (малым временем корреляции ![]() ) для повышения точности оценки запаздывания t представляет альтернативный вариант простому увеличению энергии сигнала.
) для повышения точности оценки запаздывания t представляет альтернативный вариант простому увеличению энергии сигнала.
Сужение АКФ сигнала и, значит, расширение его спектра может быть достигнуто тривиальным укорочением самого сигнала, поскольку интервал корреляции ограничен сверху длительностью сигнала: ![]() . Однако, следуя подобным путем, необходимо помнить, что укорочение сигнала потребует пропорционального увеличения пиковой мощности для сохранения неизменным отношения сигнал-шум. С другой стороны, чрезмерная излучаемая мощность резко ухудшает массо-габаритные параметры передающей аппаратуры и источника питания.
. Однако, следуя подобным путем, необходимо помнить, что укорочение сигнала потребует пропорционального увеличения пиковой мощности для сохранения неизменным отношения сигнал-шум. С другой стороны, чрезмерная излучаемая мощность резко ухудшает массо-габаритные параметры передающей аппаратуры и источника питания.
Повышение точности измерения времени запаздывания без увеличения пиковой мощности можно достичь более элегантным способом: попытаемся найти сигнал с узкой АКФ, длительность ![]() которого достаточно велика для обеспечения нужной энергии:
которого достаточно велика для обеспечения нужной энергии:
![]() .
.
Очевидно, что только технологии расширенного спектра предоставляет возможность конструирования сигнала с малым по сравнению с его длительностью временем корреляции. В случае построения подобного сигнала устраняется конфликт между величиной мгновенной мощности и точностью оценки. Необходимую энергию удается вложить в сигнал за счет его достаточной длительности T ![]() , а не большой мощности P, тогда как высокая точность измерения достигается за счет узости АКФ или, что аналогично, ширины спектра сигнала
, а не большой мощности P, тогда как высокая точность измерения достигается за счет узости АКФ или, что аналогично, ширины спектра сигнала ![]() .
.

Рисунок иллюстрирует процедуру обработки подобного входного сигнала ![]() согласованным фильтром. Поскольку отклик этого фильтра на сигнал
согласованным фильтром. Поскольку отклик этого фильтра на сигнал ![]() воспроизводит его АКФ, то, если последняя оказывается узкой
воспроизводит его АКФ, то, если последняя оказывается узкой ![]() , выходной сигнал
, выходной сигнал ![]() оказывается значительно короче входного. Именно узость АКФ гарантирует высокую точность измерения времени запаздывания сигнала, поскольку позиция остроконечного импульса может быть зафиксирована значительно более точно, чем плоского.
оказывается значительно короче входного. Именно узость АКФ гарантирует высокую точность измерения времени запаздывания сигнала, поскольку позиция остроконечного импульса может быть зафиксирована значительно более точно, чем плоского.
Следует отметить, что условие широкополосности ![]() является лишь необходимым (но не достаточным) для достижения эффекта временной компрессии при согласованной фильтрации. Синтез сигналов, сочетающих большую собственную длительность с острой АКФ, является весьма нетривиальной задачей.
является лишь необходимым (но не достаточным) для достижения эффекта временной компрессии при согласованной фильтрации. Синтез сигналов, сочетающих большую собственную длительность с острой АКФ, является весьма нетривиальной задачей.
Резюмируя, сформулируем следующий вывод. В отсутствие ограничений на пиковую мощность повышение точности в классической задаче измерения запаздывания не требует обязательного привлечения технологии расширения спектра и имеет решение на основе использования простых сигналов с достаточной энергией ![]() . В то же время указанная технология является безальтернативной всякий раз, когда пиковая мощность жестко лимитирована.
. В то же время указанная технология является безальтернативной всякий раз, когда пиковая мощность жестко лимитирована.
2.7. Оценка несущей частоты радиосигнала
Рассмотрим теперь ситуацию, в которой неизвестным информативным параметром служит несущая частота сигнала. Обычно в приложениях номинальное значение несущей частоты ![]() фиксировано и измерению полежит лишь смещение
фиксировано и измерению полежит лишь смещение ![]() частоты принятого сигнала относительно
частоты принятого сигнала относительно![]() , так что модель сигнала на входе приемника удобно записать в виде
, так что модель сигнала на входе приемника удобно записать в виде
![]() ,
,
где ![]() – комплексная огибающая сигнала, включающая линейный фазовый дрейф, обусловленный частотным сдвигом
– комплексная огибающая сигнала, включающая линейный фазовый дрейф, обусловленный частотным сдвигом ![]() , а
, а ![]() – как и ранее, мешающий параметр – случайная начальная фаза, не содержащая информации о сдвиге
– как и ранее, мешающий параметр – случайная начальная фаза, не содержащая информации о сдвиге ![]() .
.
Подобная задача столь же часто встречается на практике, как и предыдущая. Она характерна для радиолокации, где скорость объекта измеряется через оценку доплеровского сдвига частоты, устройств восстановления опорного колебания в мобильной радиосвязи второго и третьего поколений; систем автоподстройки частоты в телевизионных и вещательных ЧМ приемниках и т.п.
Вследствие частотно-временной дуальности можно опустить детальный анализ факторов, определяющих точность частотного измерения. Действительно, поскольку точность измерения запаздывания t (сдвига сигнала по оси времени) зависит (наряду с отношением сигнал-шум) от протяженности сигнала в частотной области (полосы W), то можно предположить, что точность измерения частотного сдвига F будет зависеть от протяженности сигнала во временной области, которая есть просто длительность сигнала T:
![]() ,
,
где константа a (порядка единицы, как и при оценке временной задержки) зависит от формы сигнала и способа определения длительности сигнала.
На основании рассмотренного материала можно заключить, что в случае, когда единственным информативным параметром является частота, отсутствуют какие-либо показания к привлечению широкополосных сигналов, поскольку, помимо энергии, только длительность сигнала оказывает влияние на точность оценки.
2.8. Одновременная оценка запаздывания и частоты
Обсудим теперь ситуацию, когда как временной ![]() , так и частотный
, так и частотный ![]() сдвиги принятого сигнала являются неизвестными информативными параметрами, т.е. подлежат измерению. Подобная задача соответствует многим реальным сценариям. В цифровых телекоммуникациях, например, в системах мобильной связи 2-го и 3-го поколений, прием, как правило, начинается с синхронизации местного опорного колебания с принятым сигналом. Данная операция состоит в измерении частотно-временного рассогласования локального эталона с приходящим сигналом и последующей частотно-временной подстройки первого до входа в синхронизм со вторым.
сдвиги принятого сигнала являются неизвестными информативными параметрами, т.е. подлежат измерению. Подобная задача соответствует многим реальным сценариям. В цифровых телекоммуникациях, например, в системах мобильной связи 2-го и 3-го поколений, прием, как правило, начинается с синхронизации местного опорного колебания с принятым сигналом. Данная операция состоит в измерении частотно-временного рассогласования локального эталона с приходящим сигналом и последующей частотно-временной подстройки первого до входа в синхронизм со вторым.
В отличие от скалярных параметров, фигурировавших в предыдущих параграфах, теперь оцениваемым параметром является двумерный вектор ![]() . Соответственно, модель принятого сигнала комбинирует в себе модели из 2.6 и 2.7:
. Соответственно, модель принятого сигнала комбинирует в себе модели из 2.6 и 2.7:
![]() ,
,
где ![]() – комплексная огибающая с учетом запаздывания и частотного сдвига, а
– комплексная огибающая с учетом запаздывания и частотного сдвига, а ![]() – как и ранее, неинформативная начальная фаза.
– как и ранее, неинформативная начальная фаза.
Точность измерения этих двух неэнергетических параметров полностью определяется (помимо отношения сигнал-шум) скоростью, с которой убывает сходство между рассогласованными по времени и частоте копиями ![]() и
и ![]() комплексной огибающей сигнала с ростом
комплексной огибающей сигнала с ростом ![]() . Иными словами, на точность влияет кривизна в нуле модуля коэффициента корреляции
. Иными словами, на точность влияет кривизна в нуле модуля коэффициента корреляции
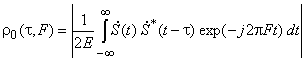 ,
,
как функции двух переменных ![]() . Эта функция, часто называемая функцией неопределенности (ФН) Вудворда, играет исключительно важную роль в теории сигналов. Геометрически ее можно представить трехмерной поверхностью над плоскостью
. Эта функция, часто называемая функцией неопределенности (ФН) Вудворда, играет исключительно важную роль в теории сигналов. Геометрически ее можно представить трехмерной поверхностью над плоскостью ![]() , имеющей максимум, равный единице, в начале координат:
, имеющей максимум, равный единице, в начале координат: ![]() . При отсутствии достоверных априорных сведений о возможных значениях
. При отсутствии достоверных априорных сведений о возможных значениях ![]() ФН должна достаточно быстро спадать в любом направлении в плоскости
ФН должна достаточно быстро спадать в любом направлении в плоскости ![]() . В качестве примера на нижеприведенном рисунке представлены два варианта функции неопределенности, причем вариант (b) является более предпочтительным, чем вариант (a), поскольку отвечает более острой функции.
. В качестве примера на нижеприведенном рисунке представлены два варианта функции неопределенности, причем вариант (b) является более предпочтительным, чем вариант (a), поскольку отвечает более острой функции.
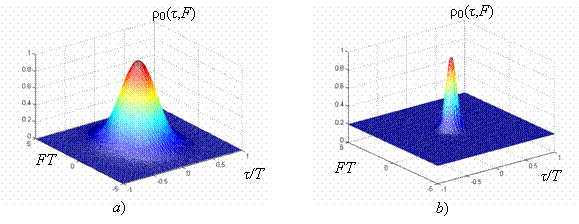
Для того, чтобы охарактеризовать остроту ![]() , нередко используют ее горизонтальное сечение (называемое диаграммой неопределенности) на некотором фиксированном уровне, например, 0.5. Протяженность диаграммы неопределенности по оси t определяется временем корреляции
, нередко используют ее горизонтальное сечение (называемое диаграммой неопределенности) на некотором фиксированном уровне, например, 0.5. Протяженность диаграммы неопределенности по оси t определяется временем корреляции ![]() сигнала. Это становится очевидным, если обратиться к сечению функции неопределенности вертикальной плоскостью
сигнала. Это становится очевидным, если обратиться к сечению функции неопределенности вертикальной плоскостью ![]() , фактически приводящей к АКФ сигнала
, фактически приводящей к АКФ сигнала
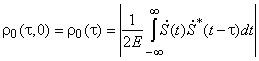
Аналогичным образом, сечение поверхности ![]() вертикальной плоскостью
вертикальной плоскостью ![]()
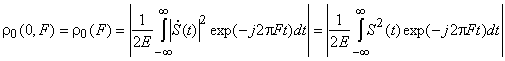
представляет собой амплитудный спектр квадрата действительной огибающей сигнала. Протяженности ![]() вдоль оси частот, называемая полосой огибающей
вдоль оси частот, называемая полосой огибающей ![]() , обратно пропорциональна длительности сигнала T и определяет точность частотного измерения. Данная характеристика устанавливает также и протяженность диаграммы неопределенности вдоль оси F. С учетом этих замечаний пример диаграммы неопределенности представлен рисунком на следующем слайде.
, обратно пропорциональна длительности сигнала T и определяет точность частотного измерения. Данная характеристика устанавливает также и протяженность диаграммы неопределенности вдоль оси F. С учетом этих замечаний пример диаграммы неопределенности представлен рисунком на следующем слайде.
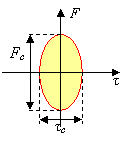
Необходимость одновременного высокоточного измерения времени и частоты требует применения сигнала с острой функцией неопределенности. Очевидно, чем острее функция неопределенности, тем меньше площадь диаграммы неопределенности, которая пропорциональна произведению ![]() . Ориентация на простые сигналы приводит к противоречию между размерами
. Ориентация на простые сигналы приводит к противоречию между размерами ![]() . Действительно, для любого простого сигнала
. Действительно, для любого простого сигнала ![]() и, следовательно,
и, следовательно, ![]() , так что достичь значительной остроты функции неопределенности вдоль одного направления (например,
, так что достичь значительной остроты функции неопределенности вдоль одного направления (например, ![]() ) невозможно иначе, как в обмен на одновременное растяжение ее в другом направлении (
) невозможно иначе, как в обмен на одновременное растяжение ее в другом направлении (![]() ).
).
Использование широкополосных сигналов открывает путь к устранению противоречия между длительностью и шириной спектра сигнала. Синтез подходящего закона угловой модуляции обеспечивает требуемую полосу сигнала ![]() (время корреляции
(время корреляции ![]() ) и, тем самым, нужную точность измерения запаздывания, тогда как длительность сигнала может быть выбрана независимо, гарантируя необходимую точность измерения частоты.
) и, тем самым, нужную точность измерения запаздывания, тогда как длительность сигнала может быть выбрана независимо, гарантируя необходимую точность измерения частоты.
Сопоставив вышеприведенное заключение с аналогичными выводами предыдущих параграфов, можно видеть, что среди всех классических задач приема, рассмотренных к этому моменту, одновременная оценка времени и частоты является первой, в которой философия расширенного спектра востребована безоговорочно. Не существует никаких иных путей бесконфликтного параллельного повышения точности измерения запаздывания и частоты, помимо использования широкополосных сигналов.

