6.4.2. Векторные подпространства
6.4.3. Пример линейного блочного кода (6, 3)
6.4.5. Систематические линейные блочные коды
6.4.7. Контроль с помощью синдромов
6.4.8.1. Синдром класса смежности
6.4.8.2. Декодирование с исправлением ошибок
Линейные блочные коды (подобные коду, описанному в примере 6.2) — это класс кодов с контролем четности, которые можно описать парой чисел (п, k) (объяснение этой формы записи приводилось выше). В процессе кодирования блок из k символов сообщения (вектор сообщения) преобразуется в больший блок из п символов кодового слова (кодовый вектор), образованного с использованием элементов данного алфавита. Если алфавит состоит только из двух элементов (0 и 1), код является двоичным и включает двоичные разряды (биты). Если не будет оговорено противное, наше последующее обсуждение линейных блочных кодов будет подразумевать именно двоичные коды.
k-битовые сообщения формируют набор из 2k последовательностей сообщения, называемых k-кортежами (k-tuple) (последовательностями k цифр), k-битовые блоки могут формировать 2n последовательности, также именуемые k-кортежами. Процедура кодирования сопоставляет с каждым из 2k Л-кортежей сообщения один из 2k л-кортежей. Блочные коды представляют взаимно однозначное соответствие, в силу чего 2k k-кортежей сообщения однозначно отображаются в множество из 2k л-кортежей кодовых слов; отображение производится согласно таблице соответствия. Для линейных кодов преобразование отображения является, конечно же, линейным.
6.4.1. Векторные пространства
Множество всех двоичных n-кортежей, Vn, называется векторным пространством над двоичным полем двух элементов (0 и 1). В двоичном поле определены две операции, сложение и умножение, причем результат этих операций принадлежит этому же множеству двух элементов. Арифметические операции сложения и умножения определяются согласно обычным правилам для алгебраического поля [4]. Например, в двоичном поле правила сложения и умножения будут следующими.
Сложение Умножение
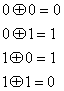
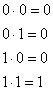
Операция сложения, обозначаемая символом “
”, — это та же операция сложения по модулю 2, которая описывалась в разделе 2.9.3. Суммирование двоичных n-кортежей всегда производится путем сложения по модулю 2. Хотя для простоты мы чаще будем использовать для этой операции обычный знак +.
6.4.2. Векторные подпространства
Подмножество S векторного пространства Vn называется подпространством, если для него выполняются следующие условия.
1. Множеству S принадлежит нулевой вектор.
2. Сумма любых двух векторов в S также принадлежит S (свойство замкнутости).
При алгебраическом описании линейных блочных кодов данные свойства являются фундаментальными. Допустим, Vi и Vj — два кодовых слова (или кодовых вектора) в двоичном блочном коде (n, k). Код называется линейным тогда и только тогда, когда (Vi Vj) также является кодовым вектором. Линейный блочный код — это такой код, в котором вектор, не принадлежащий подпространству, нельзя получить путем сложения любых кодовых слов, принадлежащих этому подпространству.
Например, векторное пространство V4 состоит из следующих шестнадцати 4-кортежей.
0000 0001 0010 0011 0100 0101 0110 0111
1000 1001 1010 1011 1100 1101 1110 1111
Примером подмножества V4, являющегося подпространством, будет следующее.
0000 0101 1010 1111
Легко проверить, что сложение любых двух векторов подпространства может дать в итоге лишь один из векторов подпространства. Множество из 2k n-кортежей называется линейным блочным кодом тогда и только тогда, когда оно является подпространством векторного пространству Vn всех n-коргежей. На рис. 6.10 показана простая геометрическая аналогия, представляющая структуру линейного блочного кода. Векторное пространство Vn можно представить как составленное из 2n n-кортежей. Внутри этого векторного пространства существует подмножество из 2k л-кортежей, образующих подпространство. Эти 2k вектора или точки показаны разбросанными среди более многочисленных 2n точек, представляющих допустимые или возможные кодовые слова. Сообщение кодируется одним из 2k возможных векторов кода, после чего передается. Вследствие наличия в канале шума приниматься может измененное кодовое слово (один из 2n векторов пространства n-кортежей). Если измененный вектор не слишком отличается (лежит на небольшом расстоянии) от действительного кодового слова, декодер может обнаружить сообщение правильно. Основная задача выбора конкретной части кода подобна цели выбора семейства модулирующих сигналов, и в контексте рис. 6.10 ее можно определить следующим образом.
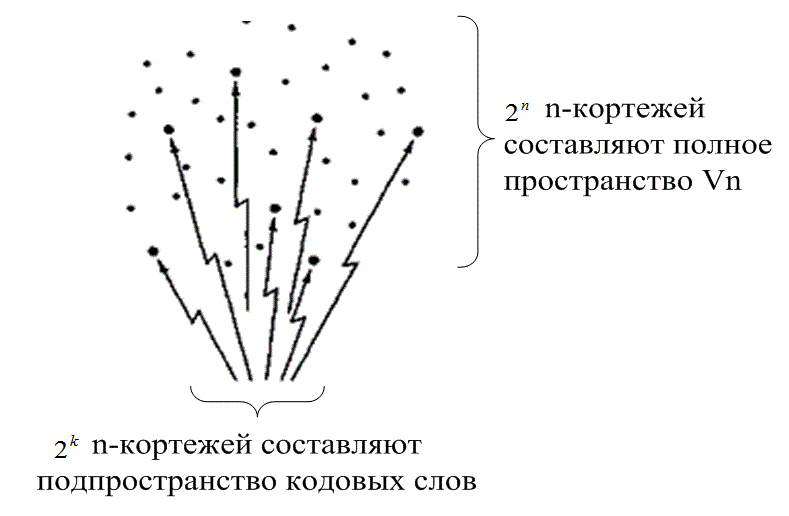
Рис. 6.10. Структура линейного блочного кода
1. Наполняя пространство Vn максимальным количеством кодовых слов, мы боремся за эффективность кодирования. Это равносильно утверждению, что мы хотим ввести лишь небольшую избыточность (избыток полосы).
2. Мы хотим, чтобы кодовые слова были максимально удалены друг от друга, так что даже если векторы будут искажены в ходе передачи, их все еще можно будет с высокой вероятностью правильно декодировать.
6.4.3. Пример линейного блочного кода (6,3)
Приведем необходимые предварительные замечания относительно кода (6,3). Он состоит из 2k = 23 = 8 векторов сообщений и, следовательно, восьми кодовых слов. В векторном пространстве V6 имеется 2n (26 = шестьдесят четыре) 6-кортежей.
Нетрудно убедиться, что восемь кодовых слов, показанных в табл. 6.1, образуют в V6 подпространство (есть нулевой вектор, сумма любых двух кодовых слов дает кодовое слово этого же подпространства). Таким образом, эти кодовые слова представляют линейный блочный код, определенный в разделе 6.4.2. Может возникнуть естественный вопрос о соответствии кодовых слов и сообщений для этого кода (6, 3). Однозначного соответствия для отдельных кодов (n, k) не существует; хотя, впрочем, здесь нет полной свободы выбора. Подробнее о требованиях и ограничениях, сопровождающих разработку кода, будет рассказано в разделе 6.6.3.
Таблица 6.1. Соответствие кодовых слов и сообщений
6.4.4. Матрица генератора
При больших k реализация таблицы соответствия кодера становится слишком громоздкой. Для кода (127,92) существует 292 или приблизительно 5 х 1027 кодовых векторов. Если кодирование выполняется с помощью простой таблицы соответствия, то представьте, какое количество памяти нужно для такого огромного числа кодовых слов! К счастью, задачу можно значительно упростить, по мере необходимости генерируя необходимые кодовые слова, вместо того чтобы хранить их в памяти постоянно. Поскольку множество кодовых слов, составляющих линейный блочный код, является k-мерным подпространством n-мерного двоичного векторного пространства (k < n), всегда можно найти такое множество n-кортежей (с числом элементов, меньшим 2k), которое может генерировать все 2k кодовых слова подпространства. О генерирующем множестве векторов говорят, что оно охватывает подпространство. Наименьшее линейно независимое множество, охватывающее подпространство, называется базисом подпространства, а число векторов в этом базисном множестве является размерностью подпространства. Любое базисное множество k линейно независимых n-кортежей V1, V2,..., Vk можно использовать для генерации нужных векторов линейного блочного кода, поскольку каждый вектор кода является линейной комбинацией V1, V2,..., Vk. Иными словами, каждое из множества 2k кодовых слов {U} можно представить следующим образом.
Здесь mi = (0 или 1) — цифры сообщения, a i = 1,..., k.
Вообще, матрицу генератора можно определить как массив размером k x n.
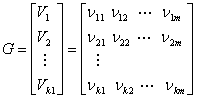(6.24)
Кодовые векторы принято представлять векторами-строками. Таким образом, сообщение m (последовательность k бит сообщения) представляется как вектор-строка (матрица 1 x k, в которой 1 строка и k столбцов).
В матричной записи генерация кодового слова U будет выглядеть как произведение m и G
U = mG, (6.25)
где умножение матриц С = АВ выполняется по следующему правилу.
Здесь А — матрица размером l х п, В — матрица размером n х т, а результирующая матрица С имеет размер l х т. Для примера, рассмотренного в предыдущем разделе, матрица генератора имеет следующий вид.
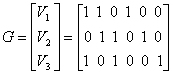(6.26)
Здесь V1, V2 и V3 — три линейно независимых вектора (подмножество восьми кодовых векторов), которые могут сгенерировать все кодовые векторы. Отметим, что сумма любых двух генерирующих векторов в результате не дает ни одного генерирующего вектора (противоположность свойству замкнутости). Покажем, как с использованием матрицы генератора, приведенной в выражении (6.26), генерируется кодовое слово U4 для четвертого вектора сообщения 110 в табл. 6.1.
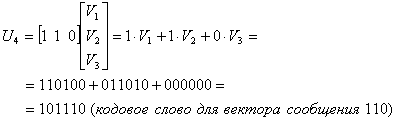
Таким образом, кодовый вектор, соответствующий вектору сообщения, является линейной комбинацией строк матрицы G. Поскольку код полностью определяется матрицей G, кодеру нужно помнить лишь k строк матрицы G, а не все 2k кодовых вектора. Из приведенного примера можно видеть, что матрица генератора размерностью 3 x 6, приведенная в уравнении (6.26), полностью заменяет исходный массив кодовых слов размерностью 8 x 6, приведенный в табл. 6.1, что значительно упрощает систему.
6.4.5. Систематические линейные блочные коды
Систематический линейный блочный код (systematic linear block code) (n, k) — это такое отображение n-мерного вектора сообщения в n-мерное кодовое слово, что часть генерируемой последовательности совмещается с k символами сообщения. Остальные (n - k) бит — это биты четности. Матрица генератора систематического линейного блочного кода имеет следующий вид.
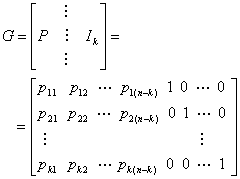(6.27)
Здесь Р — массив четности, входящий в матрицу генератора, pij = (0 или 1), а Ik — единичная матрица размерностью k x k (у которой диагональные элементы равны 1, а все остальные — 0). Заметим, что при использовании этого систематического генератора процесс кодирования еще больше упрощается, поскольку нет необходимости хранить ту часть массива, где находится единичная матрица. Объединяя выражения (6.26) и (6.27), можно представить каждое кодовое слово в следующем виде.
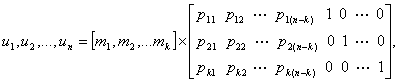
где
Для данного k-кортежа сообщения
и k-кортежа кодовых векторов
систематический кодовый вектор можно записать в следующем виде.
(6.28)
где
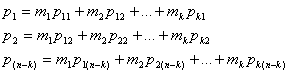(6.29)
Систематические кодовые слова иногда записываются так, чтобы биты сообщения занимали левую часть кодового слова, а биты четности — правую. Такая перестановка не влияет на свойства кода, связанные с процедурами обнаружения и исправления ошибок, поэтому далее рассматриваться не будет.
Для кода (6,3), рассмотренного в разделе 6.4.3, кодовое слово выглядит следующим образом.
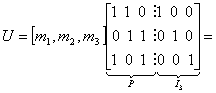(6.30)
(6.31)
Выражение (6.31) позволяет получить некоторое представление о структуре линейных блочных кодов. Видно, что избыточные биты имеют разное происхождение. Первый бит четности является суммой первого и третьего битов сообщения; второй бит четности — это сумма первого и второго битов сообщения; а третий бит четности — сумма второго и третьего битов сообщения. Интуитивно понятно, что, по сравнению с контролем четности методом дублирования разряда или с помощью одного бита четности, описанная структура может предоставлять более широкие возможности обнаружения и исправления ошибок.
6.4.6. Проверочная матрица
Определим матрицу Н, именуемую проверочной, которая позволит нам декодировать полученные вектора. Для каждой матрицы (k х n) генератора G существует матрица Н размером (n - k) х n, такая, что строки матрицы G ортогональны к строкам матрицы Н. Иными словами, GHT=0, где НT — транспонированная матрица Н, а 0 — нулевая матрица размерностью k x (n-k). НT— это матрица размером n x (n-k), строки которой являются столбцами матрицы Н, а столбцы — строками матрицы Н. Чтобы матрица Н удовлетворяла требованиям ортогональности систематического кода, ее компоненты записываются в следующем виде.
(6.32)
Следовательно, матрица НT имеет следующий вид.
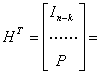(6.ЗЗ,а)
(6.33,6)
Нетрудно убедиться, что произведение UHT любого кодового слова U, генерируемого G, и матрицы HT дает следующее.
где биты четности 
определены в уравнении (6.29). Таким образом, поскольку проверочная матрица Н создана так, чтобы удовлетворять условиям ортогональности, она позволяет проверять принятые векторы на предмет их принадлежности заданному набору кодовых слов. U будет кодовым словом, генерируемым матрицей G, тогда и только тогда, когда UHT=0.
6.4.7. Контроль с помощью синдромов
Пусть 
— принятый вектор (один из 2n n-кортежей), полученный после передачи 
(один из 2n n-кортежей). Тогда r можно представить в следующем виде.
(6.34)
Здесь 
— вектор ошибки или ошибочная комбинация, внесенная каналом. Всего в пространстве из 2n n-кортежей существует 2n -1 возможных ненулевых ошибочных комбинаций. Синдром сигнала r определяется следующим образом.
(6.35)
Синдром — это результат проверки четности, выполняемой над сигналом r для определения его принадлежности заданному набору кодовых слов. При положительном результате проверки синдром S равен 0. Если r содержит ошибки, которые можно исправить, то синдром (как и симптом болезни) имеет определенное ненулевое значение, что позволяет отметить конкретную ошибочную комбинацию. Декодер, в зависимости от того, производит ли он прямое исправление ошибок или использует запрос ARQ, участвует в локализации и исправлении ошибки (прямое исправление ошибок) или посылает запрос на повторную передачу (ARQ). Используя уравнения (6.34) и (6.35), мы можем представить синдром r в следующем виде.
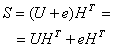(6.36)
Но для всех элементов набора кодовых слов UHT = 0. Поэтому
(6.37)
Из сказанного выше очевидно, что контроль с помощью синдромов, проведенный над искаженным вектором кода или над ошибочной комбинацией, вызвавшей его появление, даст один и тот же синдром. Важной особенностью линейных блочных кодов (весьма важной в процессе декодирования) является взаимно однозначное соответствие между синдромом и исправимой ошибочной комбинацией.
Интересно также отметить два необходимых свойства проверочной матрицы.
1. В матрице Н не может быть столбца, состоящего из одних нулей, иначе ошибка в соответствующей позиции кодового слова не отразится в синдроме и не будет обнаружена.
2. Все столбцы матрицы Н должны быть различными. Если в матрице Н найдется два одинаковых столбца, ошибки в соответствующих позициях кодового слова будут неразличимы.
Пример 6.3. Контроль с помощью синдромов
Пусть передано кодовое слово U=101110 из примера в разделе 6.4.3 и принят вектор r=001110, т.е. крайний левый бит принят с ошибкой. Нужно найти вектор синдрома S = rHT и показать, что он равен eHT.
Решение
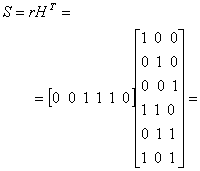
= [l, 1 + 1, l + l] = [l 0 l] (синдром искаженного вектора кода)
Далее проверим, что синдром искаженного вектора кода равен синдрому ошибочной комбинации, которая вызвала эту ошибку.
(синдром ошибочной комбинации)
6.4.8. Исправление ошибок
Итак, мы обнаружили отдельную ошибку и показали, что контроль с помощью синдромов, выполняемый как на искаженном кодовом слове, так и на соответствующей ошибочной комбинации, дает один и тот же синдром. Этот момент является ключевым, поскольку мы имеем возможность не только определить ошибку, но и (поскольку существует взаимно однозначное соответствие между исправимой ошибочной комбинацией и синдромом) исправить подобные ошибочные комбинации. Давайте так расположим 2" л-кортежей, которые представляют собой возможные принимаемые векторы, в так называемой нормальной матрице, чтобы первый ряд содержал все кодовые слова, начиная с кодового слова с одними нулями, а первый столбец — все исправимые ошибочные комбинации. Напомним, что в число основных свойств линейного кода входит то, что набор кодовых слов должен содержать член в виде вектора, состоящего из одних нулей. Каждая строка сформированной матрицы, именуемая классом смежности, состоит из ошибочной комбинации в первом столбце, называемой образующим элементом класса смежности, за которой следуют кодовые слова, подвергающиеся воздействию этой ошибочной комбинации. Нормальная матрица для кода (и, k) имеет следующий вид.
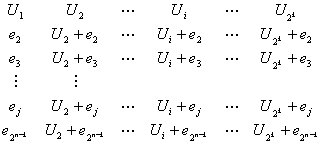(6.38)
Отметим, что кодовое слово U1 (кодовое слово со всеми нулями) имеет два значения. Оно является кодовым словом, а также может рассматриваться как ошибочная комбинация е, — комбинация, означающая отсутствие ошибки, так что r = U. Матрица содержит все 2n n-кортежей, имеющихся в пространстве Vn. Каждый n-кортеж упомянут только один раз, причем ни один не пропущен и не продублирован. Каждый класс смежности содержит 2k n-кортежей. Следовательно, всего классов смежности будет (2n/2k) = 2n-k.
Алгоритм декодирования предусматривает замену искаженного вектора (любого п-кортежа, за исключением указанного в первой строке) правильным кодовым словом, указанным вверху столбца, содержащего искаженный вектор. Предположим, что кодовое слово Ui (i = 1,..., 2k) передано по каналу с помехами, в результате чего принят (искаженный) вектор Ui + еj. Если созданная каналом ошибочная комбинация еj является образующим элементом класса смежности с индексом j = 1,...,2n-k, принятый вектор будет правильно декодирован в переданное кодовое слово Ui. Если ошибочная комбинация не является образующим элементом класса, то декодирование даст ошибочный результат.
6.4.8.1. Синдром класса смежности
Если еj является образующим элементом класса смежности или ошибочной комбинацией j-го класса смежности, то вектор Ui + еj является n-кортежем в этом классе смежности. Синдром этого n-кортежа можно записать в следующем виде.
Поскольку Ui — это вектор кода и UiHT = 0, то, как и в уравнении (6.37), мы можем записать следующее.
(6.39)
Вообще, название класс смежности (или сомножество) — это сокращение от "множество чисел, имеющих совместные свойства". Что же все-таки общего между членами каждой данной строки (класса смежности)? Из уравнения (6.39) видно, что каждый член класса смежности имеет один и тот же синдром. Синдром каждого класса смежности отличается от синдромов других классов смежности; именно этот синдром используется для определения ошибочных комбинаций.
6.4.8.2. Декодирование с исправлением ошибок
Процедура декодирования с исправлением ошибок состоит из следующих этапов.
1. С помощью уравнения S = rНT вычисляется синдром r.
2. Определяются образующие элементы класса смежности (ошибочные комбинации) е,, синдром которых равен rHT.
3. Полагается, что эти ошибочные комбинации вызываются искажениями в канале.
4. Полученный исправленный вектор, или кодовое слово, определяется как U = r + еj. Можно сказать, что в результате вычитания определенных ошибок мы восстановили верное кодовое слово. (Замечание: в арифметических операциях по модулю 2 операция вычитания равносильна операции сложения.)
6.4.8.3. Локализация ошибочной комбинации
Возвращаясь к примеру из раздела 6.4.3, мы составляем матрицу из 26 = шестидесяти четырех 6-кортежей, как это показано на рис. 6.11. Правильные кодовые слова — это восемь векторов в первой строке, а исправимые ошибочные комбинации — это семь ненулевых образующих элементов классов смежности в первом столбце. Заметим, что все однобитовые ошибочные комбинации являются исправимыми. Отметим также, что после того, как исчерпываются все однобитовые ошибочные комбинации, еще остаются некоторые возможности для исправления ошибок, поскольку учтены еще не все шестьдесят четыре 6-кортежа. Имеется один образующий элемент класса смежности, с которым ничего не сопоставлено; а значит, остается возможность исправления еще одной ошибочной комбинации. Эту ошибочную комбинацию (один из n-кортежей в оставшемся образующем элементе класса смежности) можно выбрать произвольным образом. На рис. 6.11 эта последняя исправимая ошибочная комбинация выбрана равной комбинации с двумя ошибочными битами 010001. Декодирование будет правильным тогда и только тогда, когда ошибочная комбинация, введенная каналом, будет одним из образующих элементов классов смежности.
000000 110100 011010 101110 101001 011101 110011 000111
000001 110101 011011 101111 101000 011100 110010 000110
000010 110110 011000 101100 101011 011111 110001 000101
000100 110000 011110 101010 101101 011001 110111 000011
001000 111100 010010 100110 100001 010101 111011 001111
010000 100100 001010 111110 111001 001101 100011 010111
100000 010100 111010 001110 001001 111101 010011 100111
010001 100101 001011 111111 111000 001100 100010 010110
Рис. 6.11. Пример нормальной матрицы для кода (6, 3)
Определим синдром, соответствующий каждой последовательности исправимых ошибок, вычислив еjНT для каждого образующего элемента.
Результаты приводятся в табл. 6.2. Поскольку все синдромы в таблице различны, декодер может определить ошибочную комбинацию е, которой соответствует каждый синдром.
Таблица 6.2. Таблица соответствия синдромов
Ошибочная комбинация Синдром
000000 000
000001 101
000010 011
000100 110
001000 001
010000 010
100000 100
010001 111
6.4.8.4. Пример исправления ошибки
Как говорилось в разделе 6.4.8.2, мы принимаем вектор г и рассчитываем его синдром с помощью выражения S = rHT. Затем, используя таблицу соответствия синдромов (табл. 6.2), составленную в предыдущем разделе, находим соответствующую ошибочную комбинацию, которая является оценкой ошибки (далее будем обозначать ее через 
). Затем декодер прибавляет к r и оценивает переданное кодовое слово U.
(6.40)
Если правильно вычислили ошибку: = е, тогда оценка 
совпадает с переданным кодовым словом U. С другой стороны, если оценка ошибки неверна, декодер неверно определит переданное кодовое слово и мы получим необнаружимую ошибку декодирования.
Пример 6.4. Исправление ошибок
Пусть передано кодовое слово U=101110 из примера в разделе 6.4.3 и принят вектор r = 001 ПО. Нужно показать, как декодер, используя таблицу соответствия синдромов (табл. 6.2), может исправить ошибку.
Решение
Рассчитывается синдром r.
S = [001 1 10]НT=[100]
С помощью табл. 6,2 оценивается ошибочная комбинация, соответствующая приведенному выше синдрому.
Исправленный вектор равен следующему.
Поскольку оцененная ошибочная комбинация в этом примере совпадает с действительной ошибочной комбинацией, процедура исправления ошибки дает = U. Можно видеть, что процесс декодирования искаженного кодового слова путем предварительного обнаружения и последующего исправления ошибки можно сравнить с аналогичной медицинской процедурой. Пациент (потенциально искаженный вектор) приходит в медицинское учреждение (декодер). Врач проводит серию тестов (умножение на НT), чтобы определить симптомы болезни (синдром). Допустим, врач нашел характерные пятна на рентгенограмме пациента. Опытный врач может непосредственно установить связь между симптомом и болезнью (ошибочной комбинацией). Начинающий врач может обратиться к медицинскому справочнику (табл. 6.2) для определения соответствия между симптомом (синдромом) и болезнью (ошибочной комбинацией). Последний шаг заключается в назначении соответствующего лечения, которое устранит болезнь (уравнение (6.40)). Продолжая аналогию двоичных кодов и медицины, можно сказать, что уравнение (6.40) — это несколько необычный способ лечения. Пациент излечивается в результате повторного заболевания той же болезнью.
6.4.9. Реализация декодера
Если код небольшой, например рассмотренный ранее код (6, 3), декодер может быть реализован в виде довольно простой схемы. Рассмотрим шаги, которые должны быть предприняты декодером: (1) вычислить синдром, (2) локализовать ошибочную комбинацию и (3) осуществить сложение по модулю 2 ошибочной комбинации и принятого вектора (что приводит к устранению ошибки). В примере 6.4, имея искаженный вектор, мы покажем, как с помощью последовательности этих шагов можно получить исправленное кодовое слово. Сейчас мы рассмотрим схему, показанную на рис. 6.12, где реализованы логические элементы исключающего ИЛИ и И, которые позволяют получить тот же результат для любой комбинации с одним ошибочным битом в коде (6, 3). Из табл. 6.2 и уравнения (6.39) можно записать все разряды синдрома через разряды принятых кодовых слов.
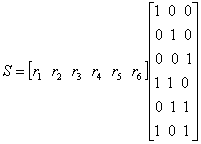
и
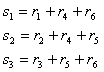
Мы используем эти выражения для синдромов при связывании схемы на рис. 6.12. Логический элемент "исключающее ИЛИ" — это и есть реализация той самой операции сложения (или вычитания) по модулю 2, поэтому он обозначен тем же символом "+". Маленький кружок в конце каждой линии, входящей в элемент И, означает операцию логического дополнения сигнала.
Искаженный сигнал подается на декодер одновременно в верхней части схемы, где происходит вычисление синдрома, и в нижней, где синдром преобразуется в соответствующую ошибочную комбинацию. Ошибка устраняется путем повторного добавления ее к принятому вектору, что дает в итоге исправленное кодовое слово.
Заметим, что с методической точки зрения рис. 6.12 составлен так, чтобы выделить алгебраические этапы декодирования — вычисление синдрома и ошибочной комбинации, а также выдачу исправленных выходных данных. В реальной ситуации код (n, k) обычно конфигурируется в систематическом виде.
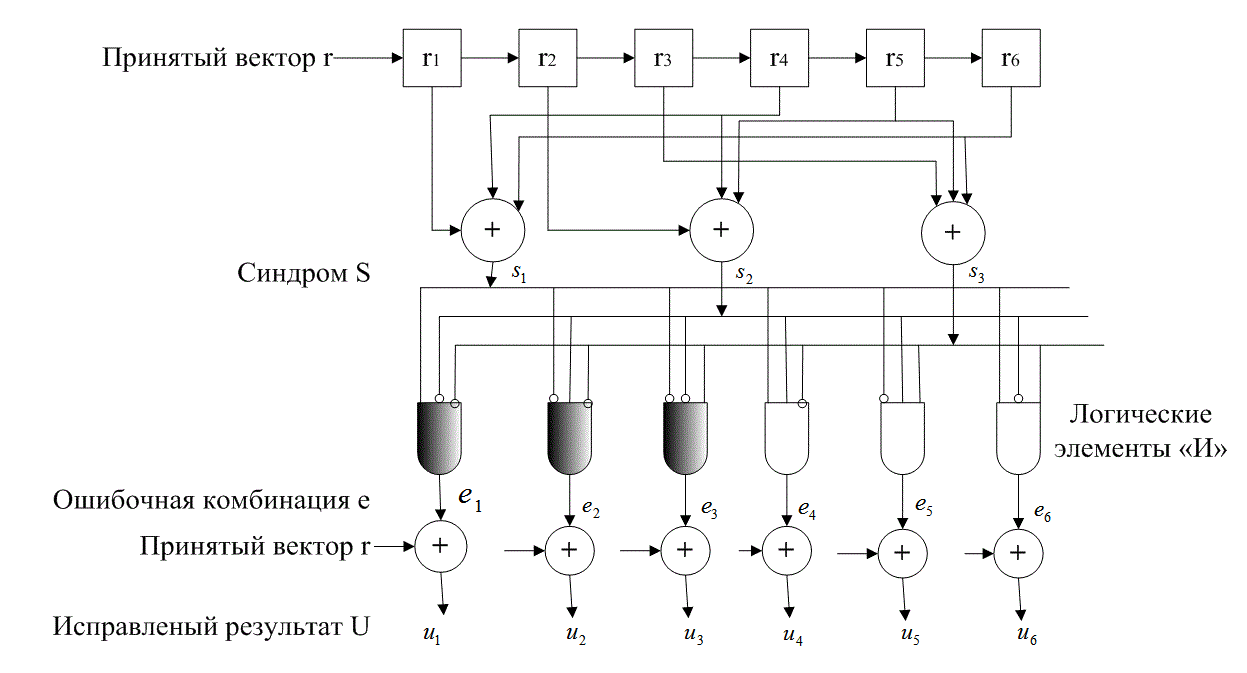
Рис. 6.12. Схема реализации декодера для кода (6, 3)
Декодеру не нужно выдавать полное кодовое слово; на выходе у него должны быть только биты данных. Поэтому схема на рис. 6.12 упрощается за счет удаления заштрихованных элементов. Для более длинных кодов такая реализация намного сложнее; в данной ситуации более предпочтительной методикой декодирования является последовательная схема, а не рассмотренный здесь параллельный метод [4]. Важно также подчеркнуть, что схема на рис. 6.12 позволяет определять и исправлять только комбинации кода (6, 3) с одним ошибочным битом. Исправление комбинаций с двумя ошибочными битами потребует дополнительной схемы.
6.4.9.1. Векторные обозначения
Выше кодовые слова, ошибочные комбинации, принятые векторы и синдромы обозначались как векторы U, e, r и S. Для упрощения записи индексы, сопутствующие конкретному вектору, в основном, опускались. Хотя, если быть точным, каждый из векторов U, е, г и S должен записываться в следующем виде.
Рассмотрим диапазон индексов j и i в контексте кода (6, 3), приведенного в табл. 6.1. Для кодового слова Uj индекс j = 1,...2k показывает, что имеется 23 = 8 отдельных кодовых слов, а индекс j= 1,...,n демонстрирует, что каждое кодовое слово составлено из п = 6 бит. Для исправимой ошибочной комбинации еj индекс j = 1,...,2n-k означает, что имеется 23 = 8 образующих элементов классов смежности (7 ненулевых исправимых ошибочных комбинаций), а индекс i= 1,...,n указывает, что каждая ошибочная комбинация составлена из п = 6 бит. Для принятого вектора r, индекс j = 1,...,2n показывает, что имеется 26 = 64 n-кортежей, прием которых возможен, а индекс i=1,...,n указывает, что каждый принятый n-кортеж состоит из п = 6 бит. И наконец, для синдрома Sj индекс j = 1,...,n - k означает, что каждый синдром состоит из n - k = 3 бит. В этой главе индексы часто опускаются, и векторы Uj, еj, гj и Sj зачастую обозначаются как U, e, r, и S. Читателю следует помнить, что для этих векторов индексы всегда подразумеваются, даже в тех случаях, когда они опущены для простоты записи.