Под оптимальной обработкой сигнала подразумевается задание исходных данных для амплитудно-частотной и фазо-частотной характеристик цифрового фильтра или аналогового фильтра.

Оптимальная фильтрация наиболее актуальна в связи с широким внедрением цифровых фильтров. Это связано с тем, что цифровой фильтр можно со сколько угодно большой точностью приблизить к рассчитанным характеристикам.

P_вх P_вых максимизировать

E_вх E_вых

n_вх(t)-шум n_вых(t)

Для выкладок будем подразумевать, следовательно, распределение входного шума равномерное.

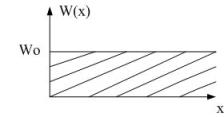
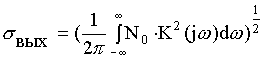
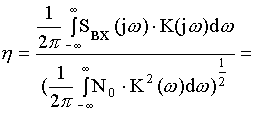
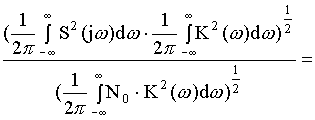
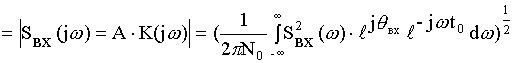
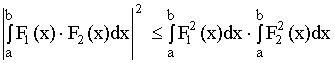
1.

2. Фазовая характеристика складывается из входного сигнала и задержки:

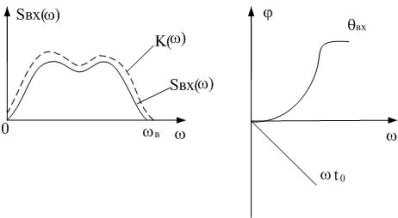
При синтезе оптимального фильтра фазовая характеристика должна быть комплексно сопряженная относительно фазовой характеристики входного сигнала.

При прохождении через оптимальный фильтр в виду того, что фазовая характеристика комплексно сопряжена с фазовой характеристикой входного сигнала, данная составляющая уничтожается.

Оптимальный фильтр не вносит фазовых искажений, его характеристика такова, что все фазовые искажения входного сигнала компенсируются.

Расчет импульсной реакции согласованного фильтра для белого шума.

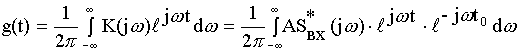
задержка

Импульсную реакцию вычислим, исходя из ОПФ. Для согласованного фильтра должна быть комплексно сопряжена величине входного спектра сигнала. Любой фильтр дает задержку выходного сигнала. Согласованный фильтр не вносит никаких фазовых искажений.

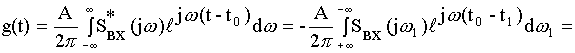
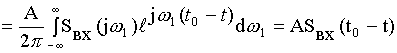
- замена

Импульсная реакция согласованного фильтра должна быть прямо пропорциональна входному сигналу во временной области, зеркально развернутому относительно оригинала согласованного фильтра. После обеливания включается каскадно четырехполюсник, у которого характеристики обратны характеристикам обелившегося фильтра.

- любая физически реализуемая цепь

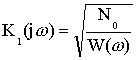
- средне-квадратическое отклонение шума

- распределение шума на выходе

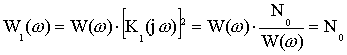- мощность шума на выходе

Функции обелившегося фильтра заключаются в том, что при прохождении через подобный фильтр свойства шума становятся подобными свойствам белого шума.

Для анализа работы согласованного фильтра нужно рассматривать не только прохождение шума, но и прохождение сигнала.

Так как распределение помехи на выходе обеляющего фильтра близко к нормальному, то тогда возможно использование математических выкладок для согласованного фильтра с белым шумом.

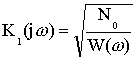
Для расчета воспользуемся:

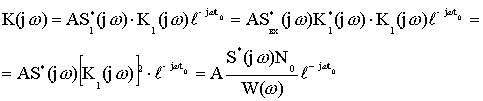
Из данного выражения следует:

1. модуль коэффициента передачи согласованного фильтра Хинчина-Винера прямо пропорционален модулю спектральной плотности входного сигнала и обратно пропорционален спектральной плотности шума или помехи

2. как и в согласованных фильтрах, для белого шума фазовая характеристика обратна фазовой характеристике входного сигнала.

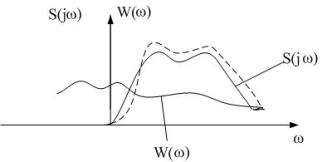
- искомая характеристика Хинчина-Винера

Приемы для синтеза согласованного фильтра Хинчина-Винера.

1. Для заданного канала рассчитывают ансамбль сигналов, при этом энергетический спектр передаваемого сигнала должен быть согласован с параметрами использованного канала связи.

2. Обычно экспериментально снимают помеховую обстановку, то есть с помощью каких-то устройств смотрят, как распределена помеха, затем снимают распределение помехи.

3. На основе расчета характеристики согласованного фильтра строят модуль коэффициента передачи, исходя из общей формулы Хинчина-Винера.

4. Зная , с помощью ОБПФ ищут отсчеты импульсной реакции.

5. Зная , любым известным способом строят структуру согласованного фильтра в цифровой форме.