При некогерентном приеме информация о фазе принимаемых сигналов не используется. Такой способ приема применяется в каналах с переменными параметрами, когда фаза сигнала случайно изменяется и ее определение вызывает значительные трудности, а также в каналах с постоянными параметрами с целью упрощения схемы приемника.

Оптимальный некогерентный приемник вычисляет модуль (огибающую) функции взаимной корреляции

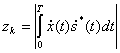
решает, что был передан тот сигнал, для которого z в некоторый момент времени ,t=t0 имеет наибольшеее значение. Пусть передавался сигнал s(t), тогда условие правильного приема этого сигнала можно записать в следующем виде: z<z или

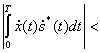
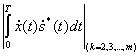(5.65)

Схема приемника, реализующего условие (5.65), приведена на рис. 5.9. Эта схема содержит т согласованных фильтров (Ф), соответствующих т

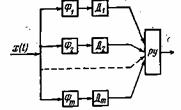
Рис. 5.9. Оптимальный некогерентный приемник m-ичных сигналов

отдельным сигналам. На выходе каждого фильтра получается напряжение, пропорциональное функции взаимной корреляции 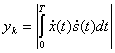. Амплитудный детектор (Д) выделяет огибающую (модуль) этой функции. Затем производится отсчет и принимается решение.

Согласно (4.25) имеем

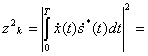
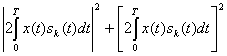
Если передавался сигнал s(t), то x(t)= s(t)+w(t) и

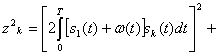
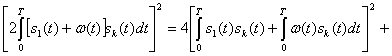
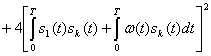
Предположим, что сигналы равновероятны, имеют одинаковую энергию и являются ортогональными в усиленном смысле (2.105). При этих условиях:

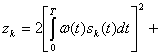
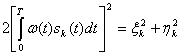
(5.66)

где

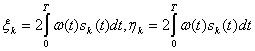Случайные величины ξ и имеют нормальное распределение s нулевым средним значением и дисперсией, равной . В этом легко убедиться так же, как это было сделано при выводе ф-лы (5.42).

Случайная величина является суммой квадратов двух независимых случайных величин и с нормальным распределением, нулевым средним значением и одинаковыми дисперсиями, равными . Такая величина, как известно, имеет распределение Рэлея (2.43). В нашем случае

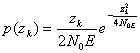(5.67)

Случайную величину можно рассматривать как квадрат длины векторной суммы постоянного вектора длиной L=2E и случайного вектора с нормально распределенными независимыми составляющими, имеющими дисперсию =. Поэтому величина подчиняется обобщенному распределению Рэлея (2.48) с плотностью вероятностей

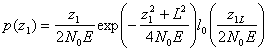(5.68)

Случайные величины есть не что иное, как огибающие напряжения в каналах без сигнала, т. е. огибающие помех. Так как помехи мы считаем гауссовыми, то этим и объясняется, что будут иметь рэлеевское распределение. Случайная величина есть огибающая суммарного колебания сигнала и помехи в канале с сигналом, поэтому она и подчиняется закону обобщенного распределения Рэлея.

Теперь можно определить вероятность ошибки при некогерентном приеме. В общем случае эта вероятность будет равна:

(5.69)

При бинарной передаче (m=2)

Для вычисления вероятности ошибки сначала вычисляется при некотором фиксированном значении вероятность того, что >. Эта вероятность выражается интегралом

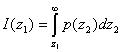
который имеет различные значения при различных . Для того чтобы найти полную вероятность >, необходимо усреднить по всем возможным значениям в соответствии с распределением Таким образом,

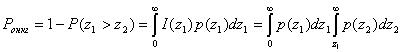(5.70)

После подстановки в (5.70) выражений и в соответствии с (5.67) и (5.68) и интегрирования получаем следующее выражение для вероятности ошибки при оптимальном некогерентном приеме двоичных сигналов:

(5.71)

где .

Для m-позиционных систем справедливо приближенное соотношение

Из уравнения ф-л (5.64) и (5.72) следует, что вероятность ошибки в многопозиционных системах Ротприближенно определяется через вероятность ошибки в соответствующей двоичной системе P. Это соотношение имеет следующий вид:

(5.73)

На рис. 5.10 приведены графики зависимости вероятности ошибки в двоичной системе с активной паузой от отношения сигнала к помехе при когерентном и некогерентном приемах. Сравнение кривых показывает, что оптимальный когерентный прием несущественно отличается по помехоустойчивости от оптимального некогерентного приема. При неоптимальном приеме и большом уровне помех (q<1) это различие, как уже отмечалось, может быть значительным.