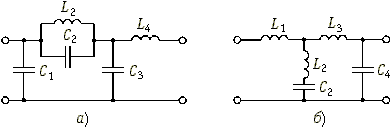Лестничные полиномиальные LC-фильтры. Любые из рассмотренных выше фильтров, как полиномиальные, так и со всплесками ослабления могут быть реализованы в виде пассивных LC-цепей.

Пассивные LC-фильтры обычно представляют собой реактивный лестничный четырехполюсник, включенный между генератором с активным внутренним сопротивление R_г и нагрузкой с активным сопротивлением R_н (рис. 17.10). Входное сопротивление реактивного четырехполюсника, нагруженного на сопротивление R_н, обозначено на рисунке Z_вх1(р).

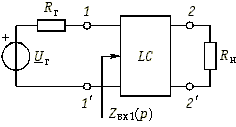
Рис. 17.10

Если фильтр со стороны зажимов 1—1' рассматривать как двухполюсник, образованный реактивным четырехполюсником и нагрузкой R_н, то, зная выражение Z_вх1(р), можно реализовать данный двухполюсник одним из известных в теории цепей методов синтеза двухполюсников. Таким образом, задача реализации фильтра сводится к реализации двухполюсника по его заданному входному сопротивлению. Идея данного подхода принадлежит С. Дарлингтону и метод реализации фильтров называется методом Дарлингтона.

На входе фильтра имеет место несогласованность, которую можно оценить, введя в рассмотрение коэффициент отражения (16.25) 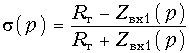(17.25)

Решая (17.25) относительно Z_вх1(р), получаем: 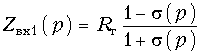(17.26)

В (17.26) неизвестным является коэффициент отражения (р). В свою очередь, коэффициент отражения (р) связан с передаточной функцией H_p(р) = w(р)/ v(р) соотношением (16.26 а): 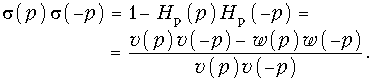(17.27)

Из (17.27) следует, что знаменатель у (р) такой же, как и у H_p(р): им является полином v(р). Остается найти нули правой части выражения (17.7) и половину из них "приписать" полиному числителя (р). Последний формируется из нулей по теореме Виета.

Пример. Реализовать фильтр нижних частот Баттерворта второго порядка в виде пассивной LC-схемы. Внутреннее сопротивление генератора 1 кОм.

В примере была получена передаточная функция Баттерворта второго порядка H_p(p) = 1/(p² + 1,41p + 1) для нормированных значений частоты = /_н = /(2×159× 10³) = / 10⁶, где _н = _п = 2f_п. Реализация нормированной передаточной функции приведет к схеме с нормированными значениями реактивных элементов (обозначим их ), которые затем необходимо денормировать для получения реальных значений.

В соответствии с (17.27) 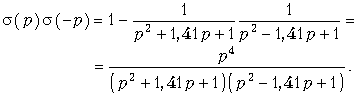Нули этой функции p_{01, 02, 03, 04} = 0. Полином числителя (р) в соответствии с теоремой Виета равен (p – p₀₁)× (p – p₀₂) = p². Отсюда (р) = p^2/(p² + 1,41p + 1).

Согласно (17.26) .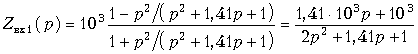

Реализацию двухполюсника со входным сопротивлением Z_вх1(p) осуществим разложением в цепную (лестничную) дробь по методу Кауэра. Представим Z_вх1(p) = 1/ Y_вх1(p) и проведем разложение проводимости: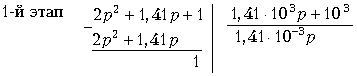

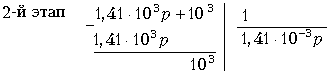
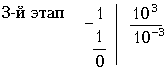
Процесс разложения закончен. Входное сопротивление Z_вх1(p), представленное цепной дробью, имеет вид:

.

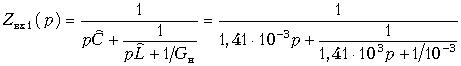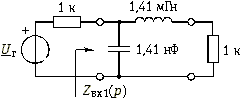
Рис. 17.11

Схема двухполюсника, входное сопротивление которого соответствует данной цепной (лестничной) дроби, приведена на рис. 17.11. Нормированные значения элементов = 1,41× 10^–3, = 1,41× 10³. Активная проводимость нагрузки не нормируется и равна G_н = 10^–3 См, т. е. сопротивление нагрузки R_н = 1 кОм. Денормировать значения элементов можно следующим образом. Комплексная проводимость нормированной емкости , откуда ненормированное значение емкости = 1,41×10^–3/10⁶ =nbsp;1,41×10^–9 Ф = 1,41 нФ.

Подобным образом комплексное сопротивление нормированной индуктивности или = 1,41×10^3/10⁶ = 1,41× 10^–3 Гн = 1,41 мГн.

Аналогично рассмотренному примеру решается задача реализации фильтра любого порядка. Например, полиномиальный ФНЧ пятого порядка (m = 5) реализуется в виде одной из двух схем, показанных на рис. 17.12, а и б. Количество реактивных элементов определяется порядком фильтра m. Отличие фильтра Баттерворта от фильтра Чебышева будет заключаться в этом случае только в разных значениях реактивных элементов, получаемых в процессе реализации соответствующих передаточных функций.

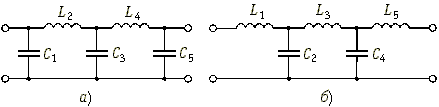
Рис. 17.12

Лестничные фильтры со всплесками ослабления. По подобной схеме осуществляется и реализация передаточных функций фильтров со всплесками ослабления (Чебышева или Золотарева). Разложение входного сопротивления таких фильтров в цепную дробь приведет к схемам, содержащим резонансные контуры, в которых резонансы происходят на частотах ₁, ₂, ... Наличие этих контуров и обеспечивает бесконечно большое затухание на частотах всплеска.

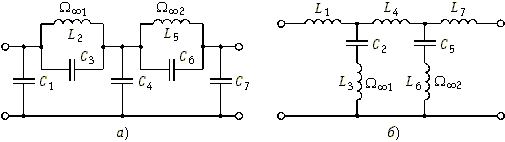
Рис. 17.13

Так, ФНЧ пятого порядка со всплесками ослабления на частотах ₁ и ₂ реализуется в виде одной из схем, приведенных на рис. 17.13, а и б. И в первой и во второй схемах контуры рассчитаны на резонансные частоты ₁ и ₂. В первой схеме в параллельных контурах происходят резонансы токов; сопротивления контуров принимают бесконечно большие значения. В результате на частотах резонансов ₁ и ₂ наблюдается "обрыв" продольных ветвей фильтра и сигнал от генератора в нагрузку не поступает, т. е. фильтр вносит бесконечно большое ослабление. Во второй схеме в последовательных контурах происходят резонансы напряжений; сопротивления контуров обращаются в нуль. Таким образом, здесь на частотах ₁ и ₂ поперечные ветви "закорачивают" нагрузку и сигнал на выход фильтра не поступает. Таким образом, имеет место бесконечно большое ослабление.

Реализация лестничных фильтров по каталогам. Из изложенного следует, что синтез фильтров представляет собой сложную процедуру, поэтому разработчики фильтров пытались облегчить ее. В результате были созданы обширные каталоги фильтров, применение которых значительно облегчает процедуру синтеза ФНЧ. Табл. 17.1 представляет собой страницу из такого каталога, где приведены нормированные элементы фильтра Золотарева четвертого порядка. В этой таблице _s, A_s, A_s – нормированная граничная частота полосы задерживания, минимальное ослабление в полосе задерживания, максимальное ослабление в полосе пропускания соответственно. Аналогичные каталоги существуют и для фильтров Баттерворта и Чебышева.

Таблица 17.1. Параметры элементов фильтров Золотарева четвертого порядка

Процедура синтеза ФНЧ с помощью каталогов может выглядеть следующим образом: 1. По формуле (17.17 а) определяем порядок фильтра m. Если число m четное, то в числитель данной формулы добавляем слагаемое в соответствии с выражением (17.40) и уточняем порядок фильтра. 2. Из каталога фильтров выбираем таблицы, соответствующие данному порядку. 3. Из данных таблиц выбираем строку, для которой с минимально возможным отклонением выполняются неравенства

Нормированные элементы данной строки и будут нормированными элементами фильтра, схема которого приведена на рисунке к данной таблице. При этом, обозначения элементов вверху таблицы относятся к схеме а, а внизу – к схеме б. Истинные значения элементов получаются путем денормирования.

Активные RC-фильтры. Фильтры, представляющие собой комбинацию пассивной RC-цепи и активного элемента, называются активными RC-фильтрами. В качестве активного элемента чаще всего используются операционные усилители с двумя входами: инвертирующим и неинвертирующим.

Реализация передаточных функций фильтров на активных RC-цепях осуществляется следующим образом. Заданную функцию H_p(p) порядка m разбивают на произведение передаточных функций не выше второго порядка, т. е. H_p(p)=H_p1(p)H_p2(p) ... H_pk(p). Каждую передаточную функцию H_pi(p) реализуют в виде ARC-звена первого или второго порядка. Схему ARC-фильтра получают путем каскадного соединения звеньев.

Пример. Пусть задана передаточная функция полиномиального фильтра Чебышева пятого порядка. .

Полюсы этой функции (корни знаменателя): р₁ = –0,177; р_2,3 = –0,143 j0,597; р_4,5 = –0,0547 j0,966. Вещественный полюс р₁ дает по теореме Виета сомножитель первого порядка (р – р₁) = р + 0,177; первая пара комплексно-сопряженных полюсов р₂ и р₃ – сомножитель второго порядка (р – р₂)×(р – р₃) = р² + 0,286р + 0,377; вторая пара полюсов р₄ и р₅ – сомножитель (р – р₄)(р – р₅) = р² + 0,110р + 0,936. Тогда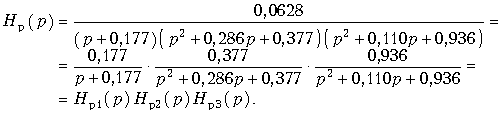

Таким образом, фильтр Чебышева пятого порядка может быть реализован двумя звеньями с передаточными функциями второго порядка и одним звеном с передаточной функцией первого порядка.

В практике проектирования активных RC-фильтров используется большое число схем, реализующих передаточные функции первого и второго порядка. Один из способов построения таких схем показан на рис. 17.14, а. Пассивная часть схемы представлена в виде цепи из элементов R и С. Между зажимами 2 и 3 включен операционный усилитель, в котором использован инвертирующий вход. Примером пассивной RC-цепи является схема, приведенная на рис. 17.14, б. Передаточная функция изображенной на рис. 17.14, б активной RC-цепи имеет вид: 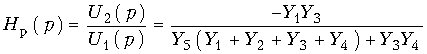(17.28)

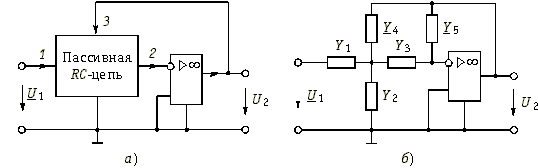
Рис. 17.14

Для реализации в виде такой цепи полиномиального фильтрового звена второго порядка с передаточной функцией 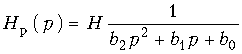(17.29)

нужно выбрать проводимости Y₁, Y₃ и Y₄ активными: G₁, G₃ и G₄, а проводимости Y₂ и Y₅ – емкостными: pC₂ и pC₅. Тогда (17.28) запишется в следующей форме: 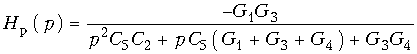(17.30)

Сопоставление коэффициентов при р в соответствующих степенях и свободных членов из (17.30), выраженных через элементы фильтра, с заданными числовыми значениями коэффициентов при р и свободных членов из (17.29) позволяет определить значения элементов фильтра.

Пример. Реализовать фильтр нижних частот Баттерворта второго порядка из примера в виде активной RC-цепи.

Передаточная функция НЧ фильтра Баттерворта второго порядка H_p(p) = 1/ (p² + 1,41p + 1). Для сопоставления с ней передаточной функции (17.30) представим последнюю в виде, когда коэффициент при p² равен 1: .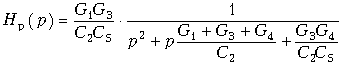

Приравнивая коэффициенты при р и свободные члены этих передаточных функций, получаем три уравнения с шестью неизвестными G₁, G₂, G₃, G₄, C₁ и C₂: ; ; .

Следует учесть, что в уравнения входят нормированные значения емкостей и , так как коэффициенты передаточной функции фильтра Баттерворта получены для нормированной частоты = /_н (где _н = '_п = 2 f_п = 2×159×10³ = 10⁶ рад/с).

Поскольку искомых величин больше, чем уравнений, зададимся частью из них. Выберем приемлемые значения проводимостей G₁, G₃ и G₄, например G₁ = G₃ = G₄ = 10^–3 См, т. е. R₁ = R₃ = R₄ = 1 кОм. Далее из второго уравнения легко получить , а из первого и третьего уравнений – . Денормированные значения емкостей 2,13 нФ, 0,47 нФ.

Схема фильтра приведена на рис. 17.15.

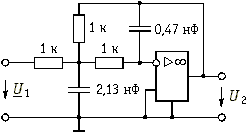
Рис. 17.15

Реализация фильтров со всплесками ослабления, передаточные функции которых описываются выражением (17.21), осуществляется так же, как и реализация полиномиальных фильтров. Передаточная функция (17.21) разбивается на произведение простейших (первого и второго порядков) передаточных функций; последние реализуются в виде фильтровых RC-звеньев первого и второго порядков, соединяемых каскадно в общую схему фильтра.

Для реализации передаточных функций второго порядка с нулем передачи H_pi(p) = (p² + a ₀)/(p² + b₁p + a ₀) используются специальные фильтровые ARC-звенья.

Более подробно методику синтеза активных RC-фильтров со всплесками ослабления можно изучить, обратившись к специальной литературе.