1. Линейность:

Если , то .

2. Запаздывание:

Если

3. Свертка:

Если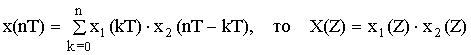

4. Умножение:

Если , то

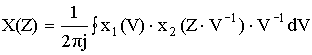
V, Z – переменные на плоскости Z.

5. Равенство Парсеваля (теорема энергии):

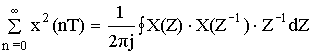
Дискретное преобразование Фурье (ДПФ).

Если сигнал x(nT) ограничен одновременно по времени некоторым значением t_и, и по частоте f_в, то он характеризуется конечным числом отсчетов N как во времени, так и в частотных областях.

Во временной области ;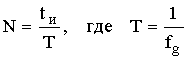

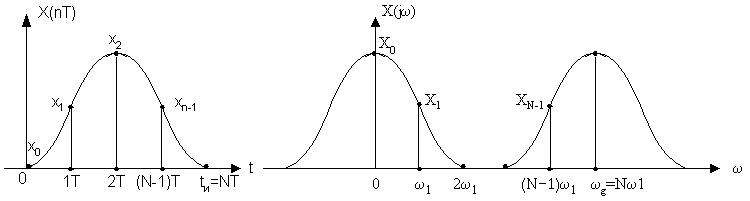
В частотной области 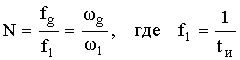– это интервал между смежными отсчетами спектра.

ω_g – тактовая частота

Отсчеты сигнала x(nT) являются коэффициентами Фурье периодической последовательности X(jω) с периодом ω_g. Это следует из формулы прямого преобразования Фурье для дискретных сигналов.

Отсчеты в частотной области (X₀,X₁,…) тоже являются коэффициентами Фурье периодической последовательности x(t) с периодом t_и.

Отсчеты во временной и частотной области связаны между собой формулами ДПФ. Формулы ДПФ следуют из формул для дискретных сигналов.

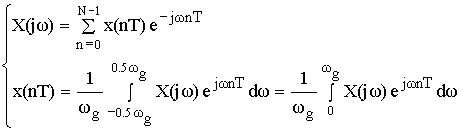
В этих формулах перейдем к дискретной переменной kω₁ от непрерывной переменной ω.

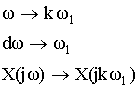
В результате такого перехода исходная пара преобразований принимает вид:

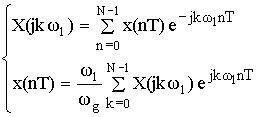
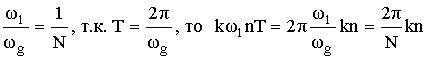
В результате формула принимает вид:

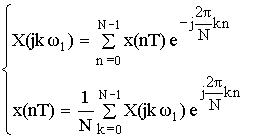прямое и обратное ДПФ

Пример:

, где a и b положительные вещественные числа a>b.

Определить отсчеты спектра

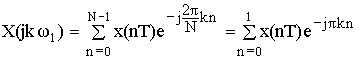
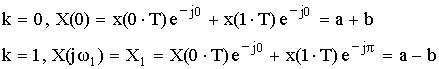
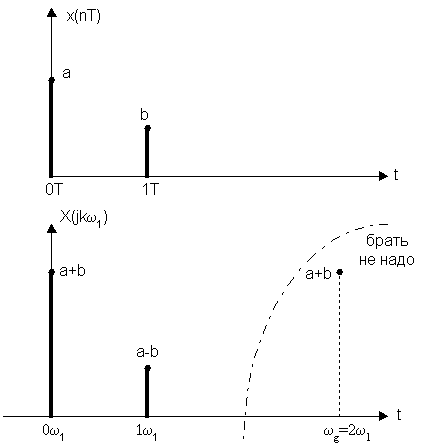
В качестве проверки по частотным отсчетам найдем временные.
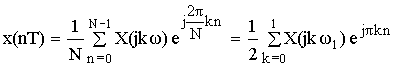