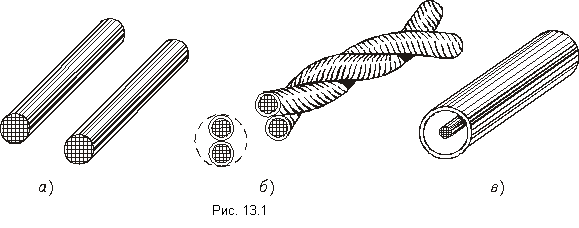
Первичные параметры. Длинные линии могут иметь самую различную конструкцию. Так, двухпроводная воздушная линия (рис. 13.1, а) состоит из параллельных неизолированных проводов, укрепленных с помощью изоляторов на специальных опорах. Симметричная кабельная цепь представляет собой два изолированных скрученных друг с другом провода, образующих так называемую пару (рис. 13.1, б). Скрученные между собой пары (или четверки), заключенные в металлическую или пластмассовую защитную оболочку, образуют симметричный кабель.
Коаксиальная пара является основой коаксиального кабеля и состоит из внутреннего цилиндра – провода сплошного сечения, помещенного в полый цилиндр (рис. 13.1, в).
Сопротивление R – это сопротивление проводов линии единичной длины. Например, для двухпроводной линии сопротивление (Ом/км)
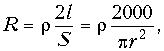
где r – удельное сопротивление материала проводов при температуре 20° С, Ом×мм2/м; l – длина линии, м; S – площадь поперечного сечения провода, мм2; r – радиус провода, мм.
При температурах, отличных от 20° С, сопротивление проводов вычисляется по формуле
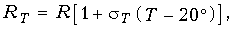
где sT – температурный коэффициент, 1/град; Т – температура, ° С. Так, сопротивление двухпроводной медной линии длиной 1 км (километрическое сопротивление) из проводов диаметром 4 мм при температуре Т= 20° С для частоты f = 0 составляет 2,84 Ом/км.
Наличие поверхностного эффекта (вытеснение тока из внутренних слоев проводника на его поверхность при увеличении частоты) приводит к увеличению сопротивления R с ростом частоты.
Индуктивность L определяется отношением магнитного потока, сцепляющегося с контуром единичной длины, к току, вызывающему этот поток. Индуктивность линии складывается из внешней и внутренней индуктивностей. Первая определяется геометрическими размерами линии и не зависит от частоты; вторая зависит от материала проводов, их диаметра и частоты.
Поверхностный эффект уменьшает внутреннюю индуктивность при возрастании частоты. Например, километрическая индуктивность двухпроводной медной цепи (Гн/км)
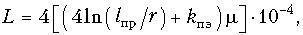
с диаметром проводов 2r = 4 мм и расстоянием между проводами lпр = 200 мм составляет на частоте f = 10 кГц (с учетом магнитной проводимости m = 1 и коэффициента действия поверхностного эффекта kпэ = 1,8) 1,89 мГн/км.
Емкость С определяется отношением заряда, приходящегося на единицу длины линии, к напряжению между проводами линии.
Для двухпроводной линии емкость (Ф/км)
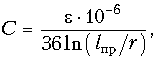
где e – диэлектрическая проницаемость вещества в пространстве между проводами. Например, километрическая емкость воздушной двухпроводной медной цепи (для воздуха e= 1) из проводов диаметром 2r = 4 мм и расстоянием между проводами lпр= 200мм составляет 7,4 нФ/км.
Проводимость G обусловлена несовершенством изоляции и представляет собой активную составляющую проводимости изоляции между проводами, отнесенную к единице длины линии. Для воздушной линии проводимость изоляции зависит от климатических условий (влажности, температуры и др.), чистоты поверхностей изоляторов и т. д.
Проводимость изоляции возрастает с ростом частоты (особенно для кабельных цепей) за счет увеличения потерь в диэлектрике. Для воздушных цепей проводимость (См/км) G = G0 +kпf, где G0 – проводимость изоляции на постоянном токе; kп – коэффициент, учитывающий потери в диэлектрике при переменном токе; f –частота.
Для кабельных цепей G =G0 +wCtgd, где tgd – тангенс угла диэлектрических потерь
После введения первичных параметров можно уточнить понятие однородной длинной линии. Однородной называется такая линия, первичные параметры которой неизменны на всей ее длине.
Уравнения передачи однородной линии. Найдем распределения напряжения и тока в линии по ее длине и во времени.
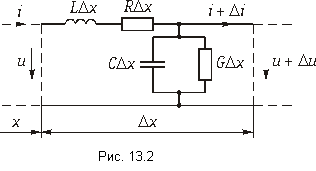
Выделим элементарный участок линии длиной Dx, находящийся на расстоянии х от начала линии (рис. 13.2). Его эквивалентную схему можно приближенно представить в виде последовательно включенных сопротивления RDx и индуктивности LDx и параллельно включенных активной проводимости GDx и емкости СDх
Таким образом, линия рассматривается как цепь с бесконечно большим числом звеньев, электрические параметры которых бесконечно малы. При стремлении Dх к нулю точность такого представления возрастает.
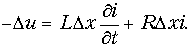
Здесь и далее используются частные производные, так как напряжение и ток являются функциями переменных t и х
Уменьшение тока на участке Dх происходит за счет ответвления тока через емкость СDх и проводимость изоляции GDx. Пренебрегая изменением напряжения как величиной второго порядка малости, можно написать
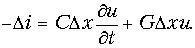 (13.1 б)
(13.1 б)Разделив обе части уравнений (13.1 а и б) на Dх и перейдя к пределу при Dх ® 0, получим дифференциальные уравнения линии:
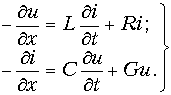
Эти уравнения называются телеграфными так как впервые были получены для линии телеграфной связи.
Будем считать, что в линии имеет место режим установившихся гармонических колебаний. Поскольку закон изменения напряжений и токов во времени известен, то из дифференциальных уравнений (13.2) остается найти лишь законы изменения амплитуд и фаз напряжений и токов с расстоянием х
Используя символический метод анализа гармонических колебаний, в котором
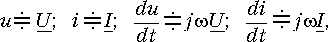
преобразуем уравнения (13.2) к виду
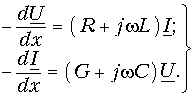
Так как комплексные действующие значения U и I являются функциями только х, уравнения записываются не в частных, а в полных производных.
Продифференцировав первое уравнение из (13.3) по х и подставив в него второе уравнение,получим
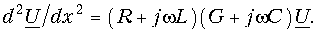
Введя обозначение
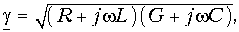
перепишем это уравнение в виде
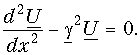
Корни характеристического уравнения p2– 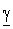 2 =0 равны p1,2 = = ±
2 =0 равны p1,2 = = ± 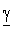 . поэтому общее решение дифференциального уравнения (13.5) для напряжения в точке х ищем в виде
. поэтому общее решение дифференциального уравнения (13.5) для напряжения в точке х ищем в виде
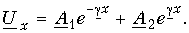
Из первого уравнения системы (13.3) имеем
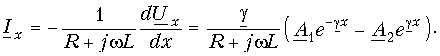 (13.6 б)
(13.6 б)Введя еще одно обозначение
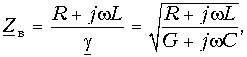
запишем решение для тока в точке х в форме
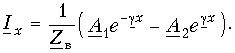 (13.7 б)
(13.7 б)Постоянные интегрирования A1 и A2 можно найти из начальных условий: при х = 0 Ux = U1 и Ix = I1, где U1 и I1 – напряжение и ток в начале линии. Тогда из (13.6 а и б) для х = 0:
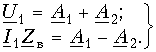
Откуда
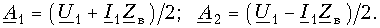
Подстановка полученных значений постоянных интегрирования в (13.6) дает следующие уравнения для определения напряжения Ux и тока Ix в произвольной точке х длинной линии
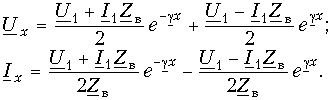
Это есть уравнения передачи однородной длинной линии. Параметры 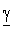 и Zв получили название коэффициента распространения и волнового сопротивления линии. Их физический смысл будет рассмотрен позже.
и Zв получили название коэффициента распространения и волнового сопротивления линии. Их физический смысл будет рассмотрен позже.
Если учесть, что

то уравнения передачи (13.8) можно переписать в более компактной форме:
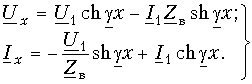
В конце линии x = l и Ux = U2 Ix = I2. Уравнения (13.9 а) примут вид
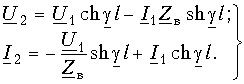 (13.9 б)
(13.9 б)Разрешая эту систему уравнений относительно напряжения U1 и тока I1 в начале линии, получаем
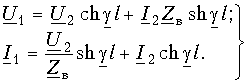 (13.9 в)
(13.9 в)Эти уравнения совпадают с известными нам уравнениями передачи (12.35) для симметричного четырехполюсника при 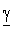 l = Гс и Zв = Zс, что вполне понятно, так как линия связи представляет собой симметричный четырехполюсник.
l = Гс и Zв = Zс, что вполне понятно, так как линия связи представляет собой симметричный четырехполюсник.

