Линейная алгебра
1. Определители, матрицы, системы линейных уравнений
1.1.1. Понятие числовой матрицы
1.1.2. Определители второго порядка
1.1.3. Подматрица, минор, алгебраическое дополнение
1.2. Решение систем линейных уравнений методом Крамера
1.3. Матрицы. Операции над матрицами
1.3.1. Умножение матрицы на число
1.3.4. Транспонирование матриц
1.3.5. Понятие обратной матрицы
1.3.6. Нахождение обратной матрицы методом Крамера
1.3.7. Алгоритм нахождения обратной матрицы методом Крамера
1.3.8. Элементарные преобразования матриц
1.3.9. Вычисление обратной матрицы с помощью элементарных преобразований
1.4. Решение системы линейных уравнений
1.5. Исследование систем линейных уравнений
1.5.2. Исследование систем линейных уравнений
1.5.3. Теорема Кронекера-Капелли
1.5.4. Однородные системы линейных уравнений
1.5.5. Свойства решений линейной однородной системы уравнений
2.1. Вектор. Линейные операции над векторами
2.1.1. Геометрический вектор. Понятие вектора
2.1.2. Линейные операции над векторами
2.1.3. Линейная зависимость векторов, теоремы о линейной зависимости
2.2.1. Скалярное произведение векторов
Примеры решения задач по алгебре
Аналитическая геометрия
3. Линейные образы. Прямая и плоскость
3.1. Системы координат и их представления. Метод координат
3.1.1. Системы координат и их представления
3.2. Уравнение прямой линии на плоскости
3.3. Уравнение плоскости в пространстве. Уравнения прямой в пространстве
3.3.1. Плоскость в пространстве
3.3.2. Нормальное уравнение плоскости
3.3.3. Условие параллельности двух плоскостей
3.4. Основные задачи на прямые и плоскости
3.4.1. Как найти точку пересечения двух прямых?
3.4.2. Как найти расстояние от точки до прямой?
3.4.3. Как разделить угол пополам?
3.4.4. Когда прямая пересекает отрезок?
3.4.5. Как найти отражённый луч?
3.4.6. Когда три прямые пересекаются в одной точке?
3.4.7. Когда три точки лежат на одной прямой?
3.4.8. Как найти треугольник по двум вершинам и центру?
3.4.9. Как найти треугольник по двум сторонам и центру тяжести?
3.4.10. Когда три плоскости пересекаются в одной точке?
3.4.11. Как найти расстояние от точки до плоскости?
3.4.12. Когда плоскость пересекает отрезок?
3.4.13. Как опустить перпендикуляр на плоскость?
3.4.14. Как найти угол между прямой и плоскостью?
3.4.15. Как найти точку пересечения прямой и плоскости?
3.4.16. Как найти плоскость, содержащую прямую и точку?
3.4.17. Как найти плоскость, содержащую прямую и параллельную другой прямой?
3.4.18. Как опустить перпендикуляр на прямую в пространстве?
3.4.19. Как найти расстояние от точки до прямой в пространстве?
1. Определители, матрицы, системы линейных уравнений
1.1. Определители и матрицы
1.1.1. Понятие числовой матрицы
Числовая матрица – прямоугольная таблица чисел, состоящая из строк и столбцов. Размеры матрицы обозначаются M * N, где M-число строк, N-число столбцов.
Пример:
A=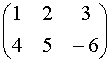 
или A=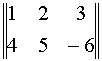
Общее обозначение:
A=
или A=
, где 
- элемент матрицы, находящийся на пересечении i-ой строки и j-ого столбца: 
Если M=N, то матрица называется квадратной. В этом случае N – ее порядок. В квадратной матрице выделяются две диагонали – главная и побочная:
. . .
. 
. . 
главная
. . 
.
побочная
. . 
. .
Пример:
A =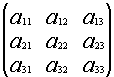 
главную диагональ образуют эл-ты:
, а побочную 
1.1.2. Определители второго порядка
Пусть дана матрица второго порядка
A=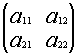 
.
Определителем второго порядка называется число, вычисляемое по правилу:
Определитель второго порядка равен произведению элементов Главной диагонали минус произведение элементов Побочной диагонали.
=
1*(-4)-6 = -10
1.1.3. Подматрица, минор, алгебраическое дополнение
Пусть дана какая-либо матрица (например, порядка 3):
А=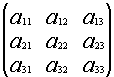
Подматрицей матрицы А называется часть этой матрицы, полученная вычеркиванием какого-либо количества строк, и(или) какого-либо количества столбцов.
Например, если вычеркнуть первую строку и второй столбец, то получим подматрицу данной матрицы:
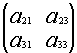
Минором 
элемента 
определителя 
называется определитель, полученный вычеркиванием i-ой строки и j-ого столбца.
Алгебраическим дополнением элемента 
называется минор, взятый со знаком “+” или “- ” в зависимости от места этого элемента в определителе.
Обозначение: 
=
Если i+j - четное число , то знак алгебраического дополнения и минора одинаковы, если нечетное , то их знаки противоположны.
Символически покажем положительные и отрицательные места в определителе:
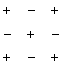или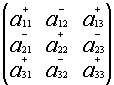 
1.1.4. Определители третьего порядка
Определителем третьего порядка называется число, вычисляемое по правилу:
= 
= 
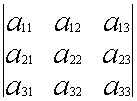Определитель третьего порядка равен сумме произведений элементов первой строки на их алгебраические дополнения.
Заменим алгебраические дополнения на миноры:
= 
= 
- 
+ 
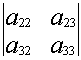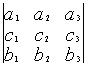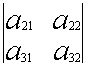
Вычисляя миноры, получим:
= 
1.1.5. Свойства определителей
Свойство 1. При замене строк на столбцы определитель не меняется.
= 
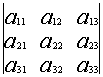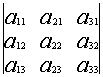
(такая операция называется транспонированием).
Следствие: строки и столбцы равноправны, т.е любые свойства или утверждения относительно строк справедливы и для столбцов и наоборот.
Свойство 2. При перестановке двух строк определитель меняет знак на противоположный.
= - 
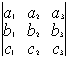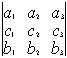
Следствие: любую строку (столбец) можно поставить первой (первым)
Свойство 3. Определитель с двумя равными строками равен нулю.
= 0
Свойство 4. Общий множитель элементов строки можно выносить за знак определителя.
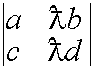
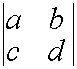
Следствие: Постоянный множитель можно внести в какую-нибудь строку
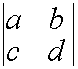
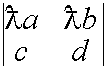
Свойство 5. Если элементы какой–либо строки состоят из двух слагаемых, то определитель можно представить в виде суммы двух определителей.
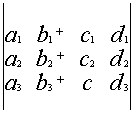
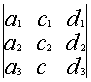
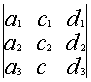
Свойство 6. Определитель не меняется, если любую строку умножить на любое число и прибавить к любой другой строке.
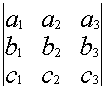
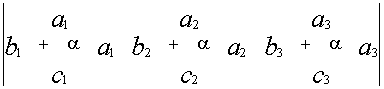
Случаи, когда определитель равен нулю:
- Все элементы какой-либо строки равны нулю
- Две строки одинаковы
- Элементы двух строк пропорциональны
1.1.6. Определители порядка n
Вычисление определителей порядка n.
Для вычисления порядка n используется метод разложения по cтроке.
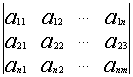
Алгебраическое дополнение получается вычеркиванием i-строки и j-столбца. Этот процесс мы будем продолжать до тех пор пока не получим определители порядка 2 или 3
Формулу (1) используют как правило при i=1
Пример:
1.2. Решение систем линейных уравнений методом Крамера
1.2.1. Понятие системы линейных уравнений
Система линейных уравнений порядка n имеет вид:
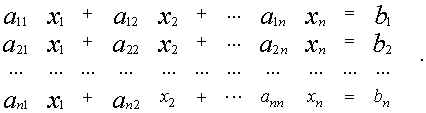
При этом числа - называются коэффициентами
при неизвестных
- свободные члены
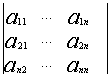Матрица называется матрицей системы
Числа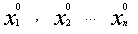 
- решение системы, если при подстановке этих чисел в систему каждое из уравнений системы превращается в верное числовое тождество.
Система линейных уравнений называется совместной, если она имеет по крайней мере одно решение.
Если система линейных уравнений не имеет решений, то система называется несовместной.
1.2.2. Формулы Крамера
Рассмотрим систему уравнений (*). И пусть А - матрица системы
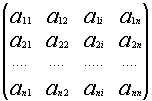
Если i – столбец заменим свободными членами, то соответствующую матрицу обозначим
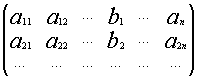
Если система линейных уравнений (*) такова, что определитель системы отличен от нуля, то система линейных уравнений имеет единственное решение, которое находится по формуле:
1.3. Матрицы. Операции над матрицами
Две матрицы A и B называются равными, если они имеют один и тот же порядок и если элементы стоящие на соответствующих местах равны.
К линейным операциям относятся:
1.3.1. Умножение матрицы на число
Для того чтобы умножить матрицу на число нужно каждый элемент матрицы умножить на это число:
1.3.2. Сложение матриц
Складывать можно только матрицы одинаковых размеров:
Свойства линейных операций
Если матрица в качестве элементов имеет нули, то такая матрица называется нулевой.
1.3.3. Произведение матриц
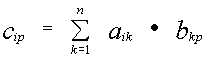
Пример:
.=
=
.=
.
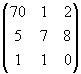
Если для матриц А и В выполняется равенство А*В=В*А, то матрицы называются перестановочными.
Если для матриц А, В, С имеет смысл операция произведения, то выполняются равенства
A(B*C)=(A*B)*C
A(B+C)=AB+AC
(B+C)A=BA+CA
1.3.4. Транспонирование матриц
Рассмотрим матрицы
AT называется транспонированной по отношению к A
Если AT получена из матрицы А заменой строк на столбцы то
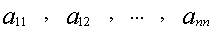называют главной диагональю
Очевидно:
Если для квадратной матрицы выполняется условие
то матрица А называется симметричной и в этом случае достаточно указать элементы, стоящие на главной диагонали и элементы, стоящие над главной диагональю.
1.3.5. Понятие обратной матрицы
Обратные матрицы существуют только для квадратных матриц. Квадратная матрица, у которой на главной диагонали стоят единицы, а
вне главной диагонали - нули, называется единичной матрицей.
Например, единичная матрица второго порядка:
Теорема.
Если А и В – квадратные матрицы одного и того же порядка n, то определитель их произведения равен произведению определителей матриц-сомножителей:
Определение обратной матрицы:
Матрица В называется обратной для матрицы А, если А и В перестановочны и А*В=В*А=Е
Обозначение обратной матрицы:
Теорема.
Если матрица А имеет обратную, то ее определитель отличен от нуля.
Доказательство.
Так как А имеет обратную матрицу, то
Воспользуемся теоремой о том, что определитель произведения равен произведению определителей.
что и требовалось доказать.
1.3.6. Нахождение обратной матрицы методом Крамера
Теорема.
Если квадратная матрица А имеет определитель отличный от нуля, то данная матрица имеет обратную.
Доказательство.
Пусть матрица А такова, что её определитель отличен от нуля.
Докажем, что существует матрица В, такая что:
*
=
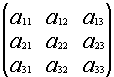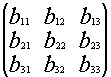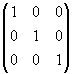
Отсюда, в частности, следует:
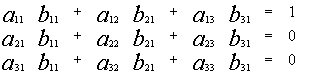
Система (3) –из трех уравнений с тремя неизвестными, и т.к. определитель системы (3) по условию отличен от нуля, то эту систему можно решить методом Крамера причем решение (3) - единственно.
Аналогично можно доказать существование и единственность всех остальных элементов матрицы В.
1.3.7. Алгоритм нахождения обратной матрицы методом Крамера
Первоначально находим определитель матрицы А и если он равен нулю, то обратной матрицы не существует.
Если определитель отличен от нуля, то находим союзную
матрицу
состоящую из алгебраических дополнений элементов матрицы А.
1.3.8. Элементарные преобразования матриц
Эквивалентные матрицы.
К элементарным преобразованиям относятся:
-
- умножение любой строки матрицы на число, отличное от нуля;
пример
= 
- к любой строке можно добавить любую другую строку, умноженную на любое число;
- перестановка двух строк.
Матрицы, полученные с помощью элементарных преобразований называются эквивалентными
А~
В, В~
С, А~
С
1.3.9. Вычисление обратной матрицы с помощью элементарных преобразований
Рассмотрим квадратную матрицу А и предположим, что
тогда используя элементарные преобразования эту матрицу можно привести к единичной матрице. Таким образом единичная матрица эквивалентна любой невырожденной матрице того же порядка.
Теорема
Если элементарные преобразования:
переводят невырожденную матрицу А в единичную, то те же самые преобразования, взятые в том же порядке, переводят единичную матрицу в обратную для A.
Доказательство:
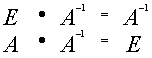
отсюда
1.4. Решение системы линейных уравнений
1.4.1. Системы линейных уравнений. Основные понятия
Система уравнений вида:
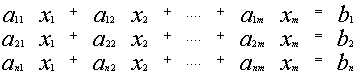
называется линейной системой из n уравнений с m неизвестными.
(aij) коэффициенты при неизвестных x1, x2,...,xm
b1,b2,...,bn - свободные члены
Матрица А системы (*) состоит из коэффициентов aij, размера n*m .
Если неизвестные и свободные члены представим в виде:
,
то систему уравнений (*) мы можем переписать в виде: 
(3)
Запись системы в виде (3) называют матричной формой записи системы линейных уравнений (*). Следует особо обратить внимание на то, что m может быть неравно n. Если m=n и матрица А является невырожденной , то из соотношения (3) вытекает: 
(4)
Равенство (4) получается умножением (3) слева на А-1. Система (*) называется совместной, если она имеет по крайней мере одно решение. В противном случае система называется несовместной.
Решить систему - означает найти все её решения.
1.4.2. Метод Гаусса
Рассмотрим систему (*):
Припишем к матрице А
матрицу-столбец В 
Припишем к матрице А матрицу-столбец
В: 
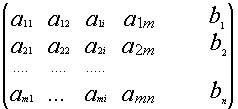
Матрица H называется расширенной матрицей системы. Матрица, у которой ниже главной диагонали стоят нули называется треугольной. Метод Гаусса (метод исключения неизвестных) состоит в том, что расширенную матрицу системы с помощью элементарных преобразований мы приводим к треугольному виду. Если у нас при этом получается матрица вида: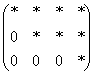 
то, система решений не имеет.
Если треугольная матрица получается вида: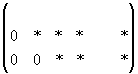
, то система имеет бесконечно много решений. При этом какие-то неизвестные
объявляются свободными, а остальные неизвестные могут быть выражены через них. Свободные неизвестные могут принимать любые значения. Если матрица примет вид: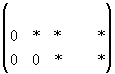
, то в этом случае система имеет единственное решение.
Пример: 
Элементарные преобразования расширенной матрицы системы, приводящие её к треугольному виду, могут быть такими:
~
~
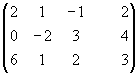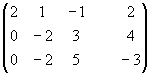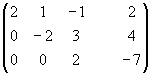
В итоге получим систему: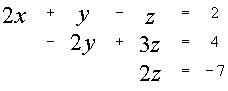
Откуда получим значения неизвестных: y = -7,25 x = 2,875 
Пример: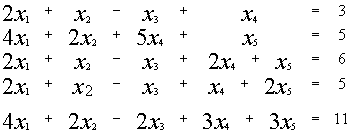 
~
~
~
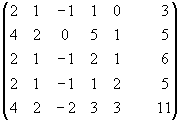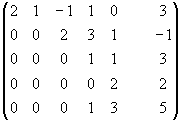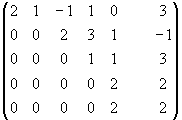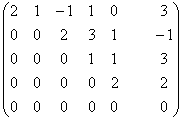
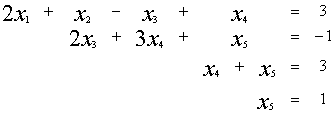
1.5. Исследование систем линейных уравнений
Рассмотрим систему линейных уравнений.
Задача: определить:
- Совместна или нет данная система
- Если совместна, то сколько имеет решений а) единственное б) бесконечное множество
Понятие ранга матрицы
А=(
) i=
j=
Возьмем в матрице К строк и К столбцов, тогда элементы матрицы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка К. Определитель этой квадратной матрицы называется минором порядка К для матрицы А.
Опр.1. Наибольший порядок минора матрицы, отличный от нуля называется рангом матрицы.
Опр.2. Число r(A)=k называется рангом матрицы А, если среди миноров порядка k есть по крайней мере один, отличный от нуля, а все миноры большего порядка равны нулю.
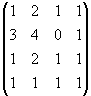М=
=0 М=
=-2
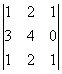0 М=
=0 М=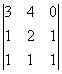
=3 Ранг равен 3.
Совершенно очевидно, что нулевой ранг имеет только нулевая матрица. Если матрица не нулевая то её ранг
1.
С другой стороны если матрица имеет порядок MxN, то r(A)
min(M,N).
1.5.1. Теоремы о ранге матриц
Теорема 1
Если матрица А эквивалентна матрице B, то ранг матрицы А равен рангу матрицы B (элементарные преобразования не изменяют ранга матрицы).
Доказательство
Для доказательства достаточно доказать, что каждое из преобразований не может изменить ранга матрицы.
1) А~B B получена умножением строки(столбца) на отличное от нуля число.
А=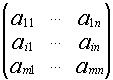
B=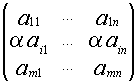
Если i-я строка не входит в выделенный минор то миноры матриц А и B совпадают. Если i-я строка входит в выделенный минор 
В=
А (по св-ву определителей). Если минор А был отличен от нуля, то В будет отличен от нуля. Таким образом умножение на отличное от нуля число не изменяет ранг матрицы.
2) A~B B получена прибавлением строк
А=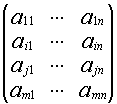
В=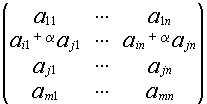
Если выбранные строки не содержат i-й строки, то соответствующие миноры матриц А и В полностью совпадают. Если минор матрицы А=0, то и минор матрицы В=0, если минор матрицы А0, то и минор матрицы В0.
Если выбранные миноры содержат i-ю и j-ю строки, тогда
М(А)=А=
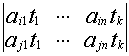
В=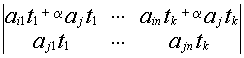
минор В получен из А путем прибавления строки.
Элементарные преобразования получаются с помощью конечного числа преобразований 1 и 2 типа и по уже доказанному на каждом из шагов ранг матрицы не меняется. Следовательно, он не изменится и за конечное число шагов. Ранг матрицы не меняется, если произведено конечное число элементарных преобразований.
Теорема 2
Ранг ступенчатой матрицы равен числу ее ненулевых строк.
Вычисление ранга матрицы
Используя утверждение доказанной теоремы, легко вычислить ранг матрицы
- с помощью элементарных преобразований матрица приводится к ступенчатому виду.
- считается число ненулевых строк ступенчатой матрицы
Ясно, что если матрица является квадратной и невырожденной, то её ранг равен порядку этой матрицы.
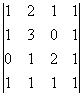
ПРИМЕР
~ 
~ 
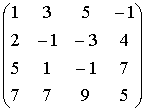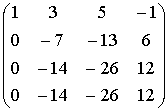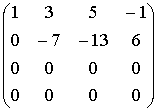
Ответ: r(A)=2
1.5.2. Исследование систем линейных уравнений
Рассмотрим систему линейных уравнений
(*)
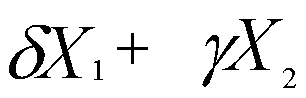
А=(
)
H=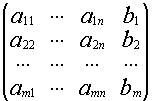
1.5.3. Теорема Кронекера-Капелли
Система ур-ний (*) совместна тогда и только тогда, когда ранг матрицы системы А равен рангу расширенной матрицы r(A)=r(H)
Если система совместна, то она имеет единственное решение, если r(A)=r(H)=n и его можно найти методами Крамера или Гаусса.
Если r(A)=r(H)=k<n, то система имеет бесконечно много решений. В этом случае n-k неизвестных объявляются свободными неизвестными (принимают любые значения), оставшиеся k неизвестных выражаются через эти свободные неизвестные.
1.5.4. Однородные системы линейных уравнений
Если в системе (*) все свободные члены 
равны нулю, то такая система является однородной.
Однородные системы всегда совместны т.к. 
=
=
=
=0 всегда является решением. Такое решение называется тривиальным.
1) 
то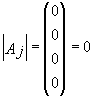 
2) Если ранг матрицы А меньше числа неизвестных,то система имеет бесконечно много решений
1.5.5. Свойства решений линейной однородной системы уравнений
1) Если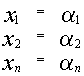 
является решением системы, то 
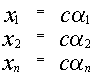также является решением.
Доказательство.
2) Если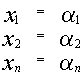 
является решением системы
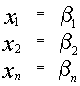также является решением той же самой системы, то и
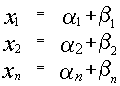также является решением системы
Доказательство.
+
откуда получим 
3) Есл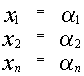и 
и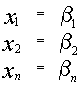 
два различных решения системы, то их линейная комбинация, равная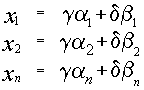 
также является решением системы.
Доказательство.
+
откуда получим 
Каждое из решений системы можно записать в виде строки матрицы
, тогда на основании свойств можно утверждать, что матрицы 
есть решения, то 
также являются решением. Минимальная возможная система решений через которую выражаются все остальные решения называется фундаментальной системой решений.
Пример.
~
~
{
{
{
{
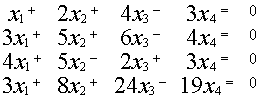
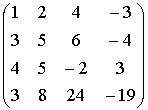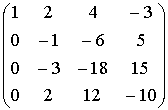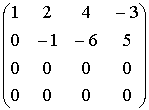
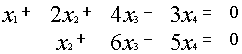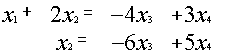
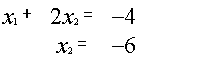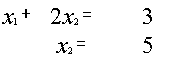
2. Векторная алгебра
2.1. Вектор. Линейные операции над векторами
2.1.1. Геометрический вектор. Понятие вектора
Вектор:
отрезок с началом в точке А и концом в точке В.
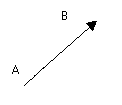Обозначается: 
Два вектора 
равны, если они совпадают при параллельном переносе.
Два вектора называются коллинеарными, если они параллельны.
Три вектора называются компланарными, если они лежат в одной плоскости.
2.1.2. Линейные операции над векторами
А) Умножение вектора на число.
Б) Сложение векторов
1) 
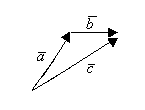
2) 
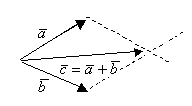
3) 
- длину вектора умножить на 
и оставить направление вектора если 
Таким образом операции обладают св-ми.
1) 
2) 
Вектор у которого начало и конец совпадают есть нулевой вектор 
3) 
4) 
5) 
6) 
7) 
8) 
Вычитание - обратное сложению.
2.1.3. Линейная зависимость векторов, теоремы о линейной зависимости
Определение 1. Система векторов 
называется линейно зависимой, если сущ. числа 
не все равные 0, такие что 
(1)
Система векторов называется линейно независимой, если равенство (1) возможно только в том случае, когда все числа =0
Выражение стоящее в левой части рав-ва (1) наз-ют линейной комбинацией векторов
Определение 2. Система векторов является линейно зависимой, если существует линейная комбинация этих векторов с неравными 0 числами, которая тождественно равна.
Теорема 1. Если система векторов содержит нулевой вектор, то данная система линейно зависима.
Доказательство. Пусть 
, тогда 
Теорема 2. Если к системе линейно зависимых векторов добавить произвольный вектор 
, то вновь полученная система будет линейно зависима.
Доказательство. Т.К. система векторов линейно зависима, то есть не все равные нулю, такие что 
(2) 
(3)
(4)
Есть 
,
0 - не все равны нулю
Следовательно система линейно зависима.
Следствие. Если к линейно зависимой системе добавить любое кол-во векторов, то полученная система будет линейно зависима.
2.1.4. Теорема о линейной зависимости двух векторов
Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство. 
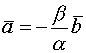
- коллинеарны
Теорема. Три вектора линейно зависимы тогда и только тогда, когда они компланарны
Доказательство. 
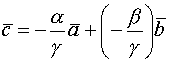
Для 
и 
пл-ть 
, что 
(или
//) и 
либо 
,
либо // ей они компланарны.
Теорема. В трехмерном пространстве любые 4 вектора линейно зависимы.
Доказательство.
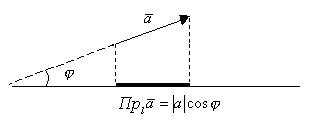
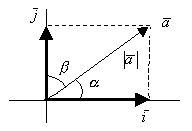
-угол между
Вектор в системе координат
Базис-максимальная упорядоченная система линейно независимых векторов.
На плоскости 2 любых неколлинеарных вектора образуют базис.
ДПБ-базис, состоящий из ортогональных единичных векторов.
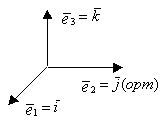
Операции над векторами в координатной форме.
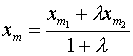
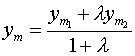
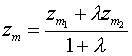
-нач.точка 
- кон.точка
направляющие косинусы
2.2. Произведение векторов
2.2.1. Скалярное произведение векторов
Определение. Скалярным произведением векторов наз-ся скалярное произведение длин этих векторов на косинус угла между ними. 
Если вектор нулевой, то все произведения - ноль
Свойства скалярного произведения
-
- Есл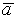и
и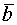 
ортогональны 
,
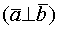то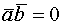
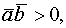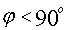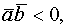если 
; 
если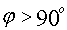 
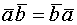(коммутативность)
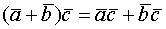(дистрибутивность)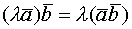
=
=
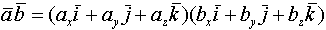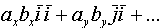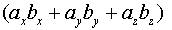
- Если
(скалярное произведение в координатах)
Условие ортогональности векторов 
Условие коллинеарности векторов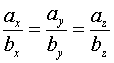 
Скалярный квадрат 
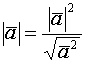
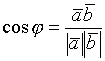
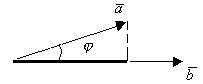
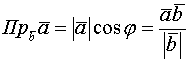
2.2.2. Векторное произведение векторов
Ориентация базиса
Декартов прямоугольный базис на плоскости
Декартов прямоугольный базис в пространстве
Правой тройкой векторов называется такая тройка, что если смотреть с конца вектора 
, то поворот от 
происходит в положительном направлении (против часовой стрелки).
Определение: Векторным произведением, 
2-х векторов называется вектор 
, такой что
1) 
- правая тройка
2) 
3) 
Свойства векторного произведения
-
- Если 2 вектора коллинеарны, их произведение =0
-
- Если поменять местами сомножители, меняется знак
(антикоммутативность)
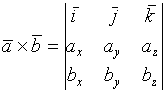
Пример.
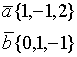
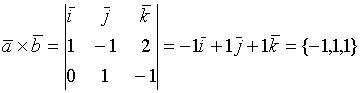
2.2.3. Смешанное произведение векторов
=
=
=
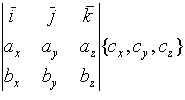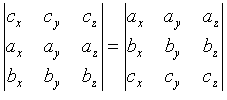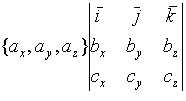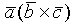
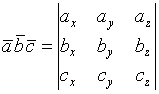
Свойства смешанного произведения
Примеры решения задач по алгебре
Задача 1.
Дана система трёх линейных уравнений. Найти решение её методом Крамера.
2x + 3y + z = 1
- x + 4y + 2z = - 1
x - 2z - 3z = - 3
Решение.
Запишем формулы Крамера: 
; 
; 
.
Здесь: D - определитель системы;
D x – определитель, полученный из определителя системы заменой первого столбца на столбец свободных членов;
D y - определитель, полученный из определителя системы заменой второго столбца на столбец свободных членов;
D z – определитель, полученный из определителя системы заменой третьего столбца на столбец свободных членов.
В нашем случае имеем:
.
.
.
.
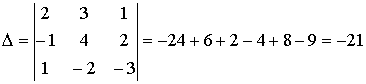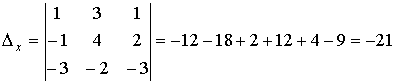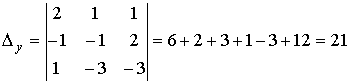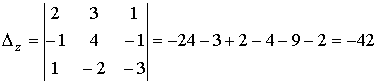Теперь найдем значения неизвестных:
; 
; 
.
Для проверки подставим найденные значения неизвестных в исходную систему и убедимся в правильности решения.
Задача 2.
Даны координаты вершины пирамиды 
. Сделать
- длину ребра
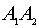. - угол между ребрам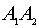и и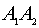
- площадь грани
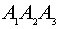
- уравнение прямой
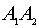
- уравнение плоскости
- объем пирамиды
,
, 
, 
Решение:
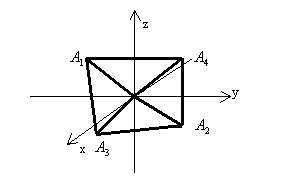
1) Длина ребра равна расстоянию между точками 
и 
или модулю
вектора 
. Расстояние между точками 
и 
вычисляется по формуле 
.
Подставляя в эту формулу исходные данные, получим 
2) Угол между ребрами будем искать, используя формулы векторной алгебры:
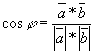
В нашем случае 
, 
.
Чтобы найти координаты вектора, из координат конца вектора следует вычесть координаты начала вектора. Таким образом,
3) Площадь треугольника можно найти, используя свойства скалярного произведения: площадь параллелограмма, построенного на векторах 
и 
численно равна модулю их векторного произведения.
В нашем случае, 
=
=
=
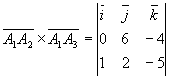Имеем, 
Итак, площадь грани
4) Уравнение прямой найдем как канонические уравнения прямой в пространстве:
,
где 
- координаты направляющего вектора прямой, а 
- координаты точки прямой. В нашем случае 
, а в качестве точки 
.
Итак, уравнение прямой 
имеет вид:
.
В общем виде:
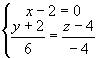или 
5) Уравнение плоскости будем искать как уравнение плоскости, проходящей через три данные точки 
,
и 
:
,
,
.
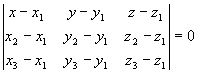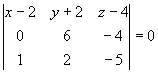Упрощая, получим: 
.
6) Объем пирамиды найдем, используя свойство смешанного произведения трех векторов – модуль смешанного произведения численно равен объему параллелепипеда, построенного на этих векторах. Соответственно
.
Найдем смешанное произведение векторов 
,
и
:
Ответы:
- длина ребр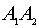а равна
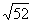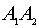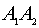(ед.) - угол между ребрами и равен
- площадь грани 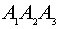равна 11.58 (кв. ед.)
- уравнение прямой (в каноническом виде ):
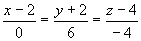
- уравнение плоскости 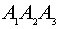(в общем виде):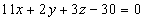
- объем пирамиды 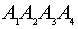равен 11 (куб. ед.).
3. Линейные образы. Прямая и плоскость
3.1. Системы координат и их представления. Метод координат
3.1.1. Системы координат и их представления
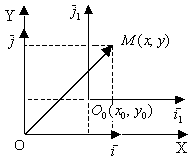
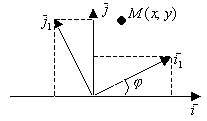
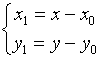параллельный перенос
=
=
; 
; 
;
; 
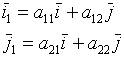
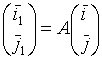
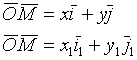
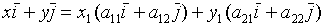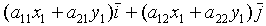
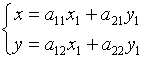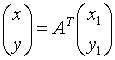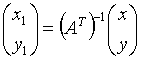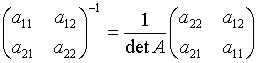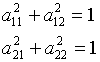
A - ортогональная, т.е.
; 
; 
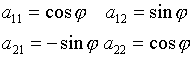
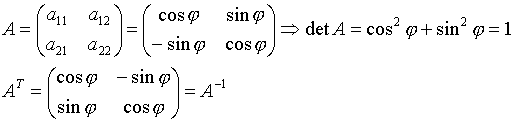
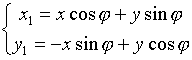(Ф-лы поворота)
Общий случай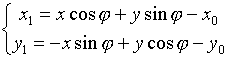 
3.1.2. Метод координат
наз-ся ур-нием линии, если каждая точка линии удовлетворяет этому ур-нию.
Алгебраической кривой наз-ся линия имеющая уравнение 
- многочлен от (x,y).
- порядок кривой (линии).
3.1.3. Теорема об инвариантности порядка
Если в некоторой ДСК кривая задается ур-нием порядка n, то в любой другой системе координат эта линия задается ур-нием такого же вида, такого же порядка.
Инвариантно - т.е. независимо от выбора системы координат.
(расстояние)
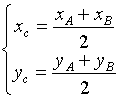середина отрезка (координат)
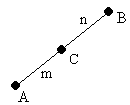
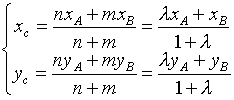формулы деления отрезка в данном отношении.
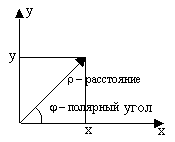
3.1.4. Полярная система координат
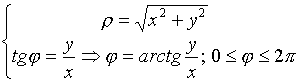
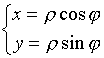
3.2. Уравнение прямой линии на плоскости
Теорема: Всякое линейное уравнение вида 
(общее уравнение прямой) определяет прямую на плоскости.
Векторное уравнение прямой.
;
;
;
;
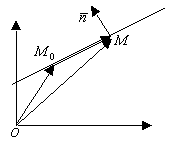
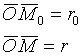- векторное уравнение прямой
- уравнение прямой проходящей через данную точку с данным нормальным вектором 
- уравнение прямой проходящей через данную точку с заданным вектором(каноническое уравнение)
;
,
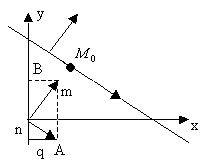
т.к.
или 
,где 
- уравнение прямой проходящей через заданную точку с данным угловым коэффициентом.
- уравнение прямой с данным угловым коэффициентом.
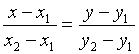- уравнение прямой проходящей через 2 заданные точки.
- уравнение прямой в отрезках
- нормальное уравнение прямой
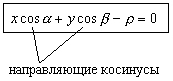
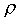- расстояние от начала координат до прямой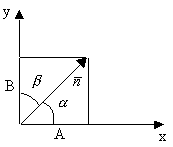 
;
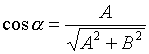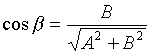
3.2.1. Параметрическое уравнение прямой
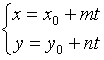
Условие параллельности двух прямых
;
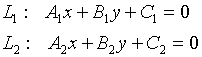
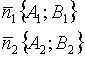
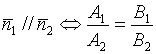Условие перпендикулярности двух прямых
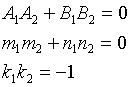
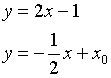
Угол между двумя прямыми 
.
=
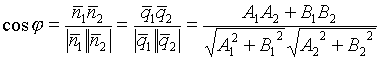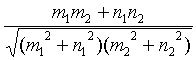
3.3. Уравнение плоскости в пространстве. Уравнения прямой в пространстве
3.3.1. Плоскость в пространстве
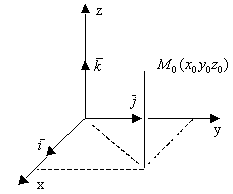
Определение: Любое линейное уравнение от 3-х переменных определяет плоскость в пространстве и обратно. 
- общее уравнение плоскости в пространстве 
- плоскость проходит через начало координат 
уравнение плоскости, проходящей через данную точку и данный нормальный вектор
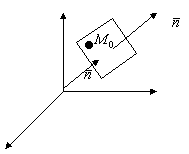
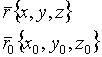
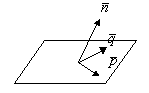
- направляющие вектора плоскости
- смешанное произведение 3-х векторов
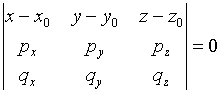- уравнение плоскости, проходящей через данную точку с данными направляющими векторами.
Пусть 
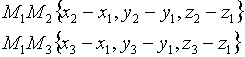
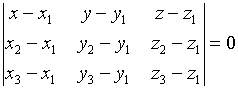x, y, z - текущие координаты
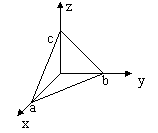
- уравнение плоскости в отрезках.
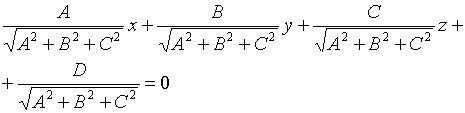
3.3.2. Нормальное уравнение плоскости
- нормальное уравнение плоскости
p - расстояние от начала координат до плоскости.
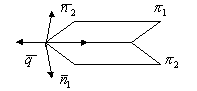
3.3.3. Условие параллельности двух плоскостей
;
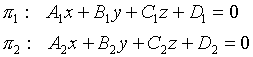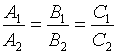
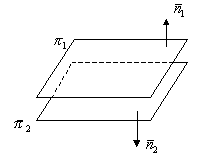
3.3.4. Условие перпендикулярности двух плоскостей
;
;
3.3.5. Угол между плоскостями
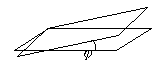
3.3.6. Прямая в пространстве
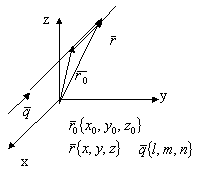
- векторное уравнение прямой в пространстве
t=
каноническое уравнение прямой
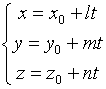- параметрическое уравнение прямой в пространстве
- уравнение прямой, проходящей через 2 данные точки
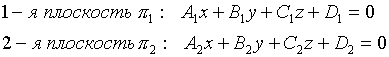
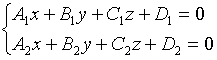- общее уравнение прямой в пространстве
Пример.
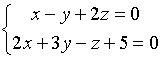
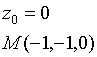
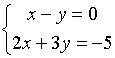
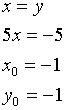
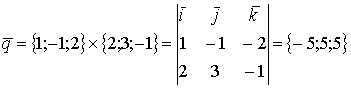
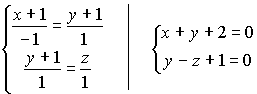
3.3.7. Условие параллельности 2-х прямых
; 
; 
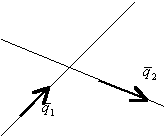
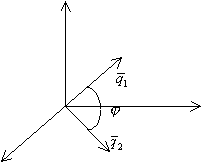
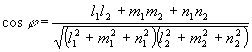
Если 
, то прямые перпендикулярны ортогонально.
3.4. Основные задачи на прямые и плоскости
3.4.1. Как найти точку пересечения двух прямых?
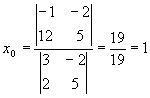
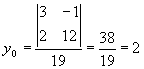
Точка пересечения (1;2).
3.4.2. Как найти расстояние от точки до прямой?
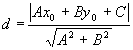
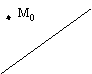
3.4.3. Как разделить угол пополам?
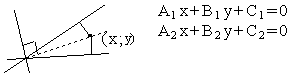
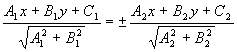
1) 
первая биссектриса "+"
2) 
вторая биссектриса
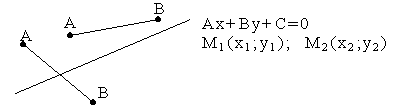
3.4.4. Когда прямая пересекает отрезок?
прямая пересекает отрезок.
Пример: 5x-y+1=0 M1(1;-1) ; M2(-3;2)
3.4.5. Как найти отражённый луч?
;
;
;
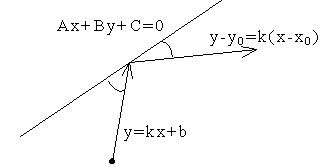
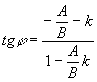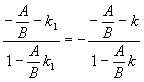
Пример:
y=2x+1 x-3y-2=0
x-3(2x+1)+2=0
-5x-1=0 
;
;
;
;
;
;
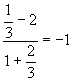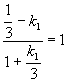3.4.6. Когда три прямые пересекаются в одной точке?
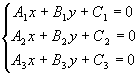имеет нетривиальное решение
;
;
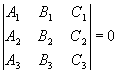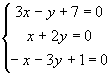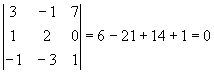
3.4.7. Когда три точки лежат на одной прямой?
A1(x1;y1) A2(x2;y2) A3(x3;y3)
;
;
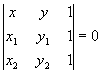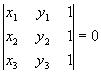
3.4.8. Как найти треугольник по двум вершинам и центру?
Дано: A, B, O - ортоцентр
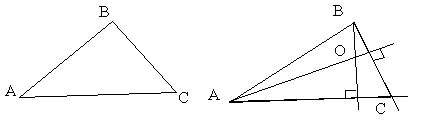
Пример: Дано: A(-5;5) B(3;1) O - ортоцентр (2;5)
;
;
x=3 4y=28
y=7 C(3;7)
3.4.9. Как найти треугольник по двум сторонам и центру тяжести?
(центру пересечения медиан)?
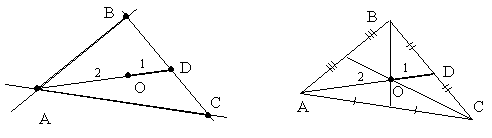
AB: 4x-5y+9=0 AC: x+4y-3=0
O(3;1) A(?;?)
По Крамеру: 
;
A(-1;1)
D - середина BC D(5;1)
BC: y-1=k(x-5) 
;
;
;
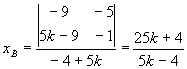
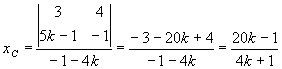
(25k+4)(4k+1)+(20k-1)(5k-4)-10(4k+1)(5k-4)
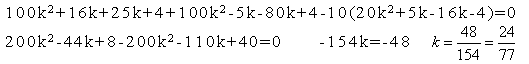
Некоторые способы решения задач
3.4.10. Когда три плоскости пересекаются в одной точке?
;
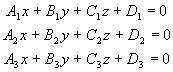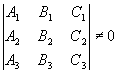
3.4.11. Как найти расстояние от точки до плоскости?
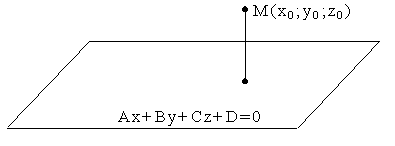
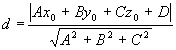
3.4.12. Когда плоскость пересекает отрезок?
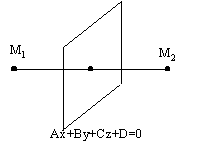
(Ax1+By1+Cz1+D)(Ax2+By2+Cz2+D)>0 M1 и M2 - по одну сторону
3.4.13. Как опустить перпендикуляр на плоскость?
3.4.14. Как найти угол между прямой и плоскостью?
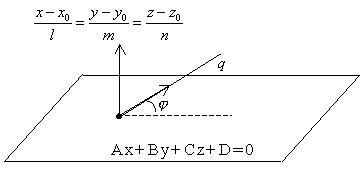
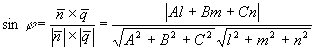угол всегда острый
3.4.15. Как найти точку пересечения прямой и плоскости?
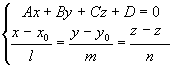2x-3y+z-5=0
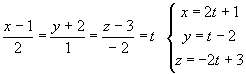2(2t+1)-3(t-2)+(-2t+3)-5=0
; 4t+2-3t+6-2t+3-5=0 ; -t+6=0 ; t=6
координаты точки пересечения
3.4.16. Как найти плоскость, содержащую прямую и точку?
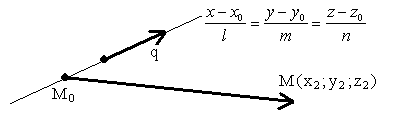
A(x-x0)+B(y-y0)+C(z-z0)=0
Пример: 
M(1;0;2) 
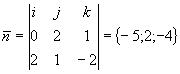; -5(x-1)+2(y-0)-4(z-2)=0
; -5x+5+2y-4z+8=0 -5x+2y-4z+13=0
3.4.17. Как найти плоскость, содержащую прямую и параллельную другой прямой?
; 
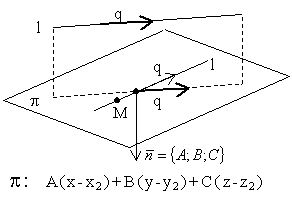
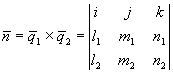
Пример: A(x-3)+B(y+4)+C(z-2)=0
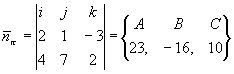
23(x-3)-16(y+4)+10(z-2)=0 ; 23x-69-16y-64+10z-20=0 ; 23x-16y+10z-153=0
3.4.18. Как опустить перпендикуляр на прямую в пространстве?
; 
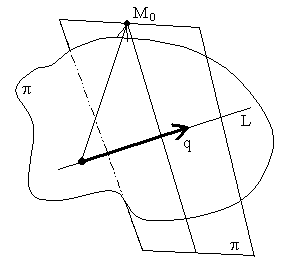
Пример:
;
Решение: 
; 
; 
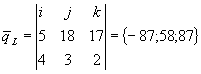3.4.19. Как найти расстояние от точки до прямой в пространстве?
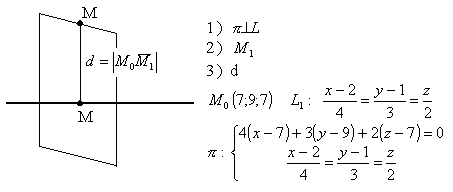
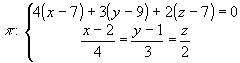
16t-20+9t-24+4t-14 ; 29t=58 t=2
3.4.20. Как найти расстояние между скрещивающимися прямыми?
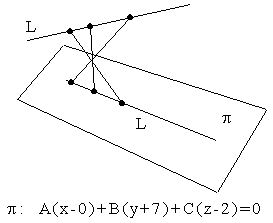Пример: 
; 
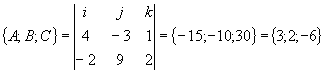; 3x+2(y+7)-6(z-2)=0
; 
3.4.21. Когда две прямые пересекаются?
; 
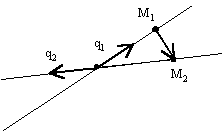
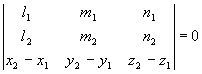
Пример: 
; 
; 
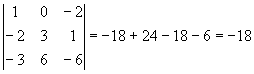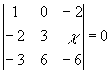
4. Кривые второго порядка
4.1. Кривые второго порядка
Геометрическое место точек называется алгебраической кривой, если левая часть его уравнения в декартовых координатах после упрощения и переноса всех членов в одну часть равенства будет многочленом относительно x и y. Степень этого многочлена, т. е. наибольшая из сумм показателей степеней x и y членов многочлена, называется порядком этой кривой. Можно доказать (это будет ниже доказано только для кривых второго порядка), что порядок алгебраической кривой не зависит от выбора осей координат на плоскости; иными словами, степень уравнения данной кривой остается одной и той же, к какой бы системе прямоугольных координат ее ни относить.
Всякое уравнение вида 
, т. е. уравнение первой степени относительно x и y, всегда определяет на плоскости некоторую прямую; таким образом, кривые первого порядка – это прямые линии.
К кривым второго порядка относятся эллипс, частным случаем которого является окружность, гипербола и парабола. Кроме того, в некоторых случаях уравнение второй степени относительно x и y может определять две прямые, точку или мнимое геометрическое место.
Кривые второго порядка – эллипс, гипербола и парабола – играют большую роль в прикладных вопросах. Напомним, что планеты солнечной системы в соответствии с первым законом Кеплера движутся вокруг Солнца по эллипсам; по эллипсам же движутся вокруг планет их спутники (в частности, искусственные спутники Земли); наконец, кометы, зашедшие в солнечную систему из мирового пространства, могут двигаться вокруг Солнца либо по эллипсам, либо по параболам, либо по гиперболам в зависимости от значения скорости, с которой комета приближается к Солнечной системе.
Кривые второго порядка начнем изучать с простейших из них – окружности.
Окружность
Как известно, уравнение окружности радиуса 
с центром в точке 
имеет вид:
(3.1).
Если в этом уравнении раскрыть скобки и перенести 
в левую часть равенства, то уравнение примет вид:
(3.1`).
Геометрический смысл уравнения не изменится, если все его члены умножить на один и тот же, отличный от нуля и не зависящий от 
и 
множитель 
;
введем обозначения – 
,
– 
, 
.
Уравнение (3.1') запишется тогда в виде:
(3.2).
Возникает вопрос: всякое ли уравнение вида (3.2) является уравнением некоторой окружности?
Чтобы ответить на этот вопрос, проделаем обратное преобразование уравнения (3.2) к виду (3.1), считая коэффициенты A, D, E и F произвольными (но 
).
Разделим все члены уравнения (3.2) на А и введем обозначения: 
, 
, 
; тогда уравнение (3.2) примет вид:
(3.2`).
Дополняя члены с x и y до полных квадратов и перенося член 
направо, придадим уравнению (3.2') вид:
(3.3).
Правая часть последнего уравнения может быть числом положительным, отрицательным или нулем.
1. Если 
, то положим 
.
Уравнение (3.3) запишется в виде:
(3.3`)
и является, как известно, уравнением окружности радиуса R с центром в точке 
.
2. Если 
, то уравнение (3.3) принимает вид:
(3.3``).
Ему удовлетворяют только значения 
, 
(сумма двух квадратов может быть равна нулю только тогда, когда одновременно равен нулю каждый из них); таким образом, уравнению (3.3'') удовлетворяет единственная точка плоскости .
Но, впрочем, можно говорить, что уравнение (3.3'') и в этом случае является уравнением окружности, но окружности, выродившейся в точку (окружности с нулевым радиусом).
3. Если 
, то полагая 
, приводим уравнение (3.3) к виду:
(3.3```).
Поскольку сумма квадратов двух вещественных чисел не может быть числом отрицательным, то на плоскости xOy не существует точек, которые удовлетворяли бы уравнению (3.3''').
Поэтому уравнение (3.3''') не определяет никакой кривой; иногда говорят, впрочем, что уравнение (3.3''') является уравнением мнимой окружности.
Только учитывая это последнее замечание, можно говорить, что уравнение (3.2) всегда определяет окружность (вещественную, выродившуюся в точку или мнимую).
Примеры.
1. Уравнение x2 + y2 – 4x + 6y – 12 = 0 приводится к виду (x – 2)2 + (y + 3)2 = 25 и определяет окружность радиуса R = 5 с центром в точке С(2;–3).
2. Уравнение x2 + y2 + 2x + 1 = 0 приводится к виду (x + 1)2 + y2 = 0 и определяет единственную точку С(–1;0).
3. Уравнение x2 + y2 + 4x + 2y + 7 = 0 приводится к виду (x + 2)2 + (y + 1)2 = – 2 и никакой вещественной кривой не определяет (мнимая окружность).
4.2. Эллипс
Эллипсом называется геометрическое место точек плоскости, сумма расстояний которых от двух данных точек этой же плоскости, называемых фокусами эллипса, постоянна.
Пусть фокусами эллипса являются точки F1 и F2, а М – некоторая точка, принадлежащая эллипсу. По определению эллипса для любой его точки М имеем:
(3.4)
где через 
обозначена упоминаемая в определении эллипса постоянная величина. Введем обозначение 
; очевидно, что 
( – сумма двух сторон треугольника 
, а 
– его третья сторона).
Для вывода простейшего уравнения эллипса выберем следующее расположение координатных осей. Начало координат О поместим в середину отрезка 
, а за ось 
примем прямую, проходящую через фокусы 
и 
, ось 
направим перпендикулярно к оси в точке 
.
При таком выборе осей координаты фокусов будут 
, 
; произвольную точку эллипса обозначим через 
.
Имеем:
, 
(3.5),
а подставляя эти значения в уравнение (3.4), находим:
(3.6).
Получено уравнение эллипса. Для преобразования уравнения к более простому виду перенесем корень второй степени в правую часть равенства и возведем обе части равенства в квадрат (одновременно раскрыв скобки):
(3.7).
Перенося в этом уравнении радикал в левую часть, а все остальные члены – в правую часть равенства, после привидения подобных членов и сокращения на общий множитель найдем:
(3.8).
Снова возведем в квадрат обе части уравнения:
(3.9).
Перенесем теперь члены с текущими координатами в левую часть равенства, а постоянные члены – в правую:
(3.10).
Наконец, разделим левую и правую части на 
:
(3.11).
Так как 
, то можно положить 
; тогда окончательно получим следующую простейшую (ее называют канонической) форму уравнения эллипса:
(3.12).
Можно доказать, что уравнение (3.12) равносильно исходному уравнению (3.6).
Исследуем форму эллипса по его уравнению. Прежде всего заметим, что каждое из двух слагаемых левой части уравнения (3.12) не превосходит единицы, поскольку их сумма (а они оба положительны) равна единице:
, 
;
отсюда найдем, что для всех точек эллипса:
, 
, (3.13)
т. е. что эллипс целиком лежит внутри прямоугольника, определяемого неравенствами (3.13).
Далее заметим, что уравнение (3.12) сохраняет вид, если заменить на 
или 
на 
(поскольку x и y входят в уравнение лишь во второй степени). Из этого следует, что если на эллипсе лежит некоторая точка 
, то одновременно с нею на эллипсе лежат и три точки 
, 
и 
, симметричные с точкой М соответственно относительно оси Ox , оси Oy и начала координат. Это означает, что эллипс имеет оси координат своими осями симметрии и поэтому для его построения достаточно построить его дугу, лежащую, например, в I четверти.
Решим уравнение (3.12) относительно y:
(3.14).
Для построения дуги эллипса, лежащей в I четверти, надо в правой части (3.14) взять знак плюс и изменять x только от 0 до a:
, 
(3.14`)
Из этого уравнения следует:
1) при 
;
2) при возрастании x от 0 до а y убывает от b до 0; 3) при 
.
Это позволяет нам построить дугу эллипса, лежащую в I четверти, и по соображениям симметрии весь эллипс.
Познакомимся с принятой в аналитической геометрии по отношению к эллипсу терминологией.
Отрезки 
и 
осей симметрии эллипса, принятых нами з оси координат, называют соответственно большой и малой осями эллипса; их длины равны соответственно 2a и 2b (
, так как 
); половину их длин – числа a и b – часто называют большой и малой полуосями эллипса. Точка О пересечения осей симметрии эллипса называется его центром. Концы большой и малой осей эллипса – точки 
, 
, 
, 
– называют его вершинами.
Форма эллипса зависит от величины соотношения 
длин его малой и большой полуосей: чем больше это соотношение, тем эллипс будет менее "сплющенным", менее сжатым; при 
эллипс, как легко установить по его уравнению (3.12), превращается в окружность; в самом деле, в этом случае уравнение (3.12) превращается в уравнение:
(3.15),
т. е. в уравнение окружности радиуса а с центром в начале координат.
В качестве характеристики формы эллипса в аналитической геометрии чаще пользуются не соотношением его полуосей , а другой величиной – отношением половины расстояния с между фокусами эллипса к его большой полуоси а, которое называют эксцентриситетом и обозначают греческой буквой "эпсилон" (
):
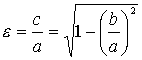(3.16).
Так как 
, то эксцентриситет для различных эллипсов может меняться в пределах от 0 до 1: 
; чем больше эксцентриситет, тем больше расстояние от центра эллипса до его фокусов и тем более сплющен эллипс; чем ближе эксцентриситет к нулю, тем больше форма эллипса приближается к окружности. (Если положить 
, то эллипс превращается в окружность; если положить 
, эллипс превращается в свою собственную большую ось).
Если по уравнению эллипса (3.12) нужно построить не только сам эллипс, но и отметить на чертеже положение его фокусов 
и 
, то полезно запомнить. Что расстояния от фокусов эллипса до концов 
и 
его малой оси равны длине большой полуоси эллипса а:
.
Это сразу следует из основного соотношения, связывающего величины a, b и с:
(3.17).
Пример.
Найти простейшее уравнение и построить его, если его большая ось расположена на оси Ox симметрично относительно начала координат и имеет длину 
, а эксцентриситет эллипса 
.
Решение. Пользуясь формулой (3.16), находим с:
.
Затем по формуле (3.17) определяем 
.
Зная теперь a и b, получаем простейшее уравнение эллипса:
.
Построение этого эллипса по его уравнению рекомендуем читателю сделать самостоятельно.
Рассмотрим теперь уравнение
, в котором 
.
Очевидно, отнесенный к системе координат, в которой оси Ox и Oy поменялись ролями: большая ось и фокусы этого эллипса лежат на оси Oy, а малая ось – на оси Ox (рис. 3.3). Следует лишь помнить, что для такого эллипса 
и 
.
Координаты фокусов такого эллипса: 
и 
.
4.3. Гипербола
Гиперболой называется геометрическое место точек плоскости, разность расстояний которых от двух данных точек той же плоскости, называемых фокусами гиперболы, постоянна.
Для вывода простейшего уравнения гиперболы расположим оси координат по отношению к ее фокусам и так же, как мы это делали в предыдущем параграфе для эллипса. Сохраним для гиперболы те же обозначения: 2а для постоянной величины, упоминаемой в определении гиперболы, 2с для расстояния между фокусами и . Координаты фокусов те же, что и для эллипса в предыдущем параграфе: 
и 
.
Возьмем произвольную точку 
, лежащую на гиперболе. По определению гиперболы для точек кривой, лежащих в I и IV четвертях имеем:
(3.18),
а для точек, лежащих во II и III четвертях:
(3.18`).
Заметим, что для гиперболы в отличие от эллипса 
(2а есть разность двух сторон треугольника 
, а 2с – его третья сторона). Выражая через координаты точек 
, 
и 
длины отрезков 
и 
оба равенства (3.18) и (3.18') можно записать в виде:
(3.19).
Производя над этим уравнением те же преобразования, что и над уравнением (3.6) в случае эллипса (см. § 4.2), мы в конечном счете придем
к тому же самому уравнению (3.10):
,
в котором, однако, теперь 
.
(Рекомендуется читателю произвести это преобразование самостоятельно.)
Деля левую и правую части уравнения (3.10) на 
и учитывая, что теперь , запишем результат в виде:
(3.20).
Наконец, полагая 
, получим окончательно простейшее (каноническое) уравнение гиперболы:
(3.21).
Можно доказать, что равенство (3.21) равносильно объединенному равенству (3.19).
Для построению гиперболы по ее уравнению (3.21) заметим прежде всего, что первый член левой части этого уравнения не меньше его правой части, т. е. единицы (поскольку из 
вычитается неотрицательная величина 
): 
.
Отсюда 
.
Таким образом, в вертикальной полосе между параллельными оси Oy прямыми 
и 
точек кривой нет.
Отмечаем далее, что, так же как и для эллипса, оси координат служат осями симметрии гиперболы, так как в уравнении (3.21) x и y входят лишь в четных степенях. Поэтому достаточно построить часть гиперболы, лежащую в I четверти.
Решим уравнение гиперболы (3.21) относительно y: 
,
выберем в правой части знак плюс, поскольку в I четверти 
:
, 
(3.22).
При 
; при возрастании x возрастает и y: ветвь гиперболы, подымаясь от оси Ox, уходит на плоскости все дальше и дальше, или, как говорят в геометрии, уходит "в бесконечность". Но при этом, как нетрудно показать, ветвь кривой все ближе и ближе подходит к прямой 
.
В самом деле, разность между ординатами точек этой прямой и гиперболы (обозначим ее через 
), соответствующих одному и тому же значению абсциссы х, имеем следующее выражение:
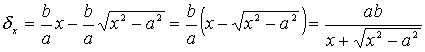(3.23)
Из последнего выражения видно, что когда х неограниченно возрастает, то , оставаясь положительным, стремится к нулю, что и подтверждает высказанную нами мысль: ветвь гиперболы, лежащая в I четверти неограниченно приближается (и притом снизу, так как 
) к прямой 
, когда абсцисса х точки гиперболы неограниченно возрастает. Такие прямые, к которым неограниченно приближаются уходящие в бесконечность ветви кривых, называются асимптотами этих кривых.
Таким образом, прямая является асимптотой гиперболы. В силу симметрии гиперболы у нее есть и вторая асимптота: 
. Наличие асимптот и соображения симметрии позволяют нам построить всю гиперболу (рис. 5): кривая состоит из двух не смыкающихся ветвей, лежащих в углах между прямыми и и неограниченно приближаются к этим прямым.
В отношении гиперболы используется следующая терминология.
Отрезок 
называют вещественной, а 
– мнимой осью гиперболы; их длины равны соответственно 2а и 2b (а – вещественная полуось, b – мнимая полуось). Точки гиперболы 
и 
, лежащие на вещественной оси, – вершины гиперболы. Точка О – центр гиперболы. Изображенный на рис. 3.5 пунктиром прямоугольник 
с центром в точке О и сторонами 
, и 
, параллельными осями симметрии гиперболы, называют осевым прямоугольником гипербол; его построение облегчает построение гиперболы; сама гипербола касается вертикальных сторон этого прямоугольника в их серединах, являющихся вершинами гиперболы.
Для построения фокусов гиперболы и полезно знать, что основное соотношение между величинами 
, 
и 
у гиперболы можно записать в виде:
(3.24).
Поэтому расстояние от центра гиперболы до ее фокуса 
равно половине длинны диагонали осевого прямоугольника 
: в прямоугольном треугольнике 
катеты 
, 
, а следовательно, его гипотенуза 
.
Форма гиперболы зависит от угла наклона асимптоты к вещественной оси, т. е. от величины отношения 
: чем эта величина меньше, тем меньше угол между асимптотами, в котором заключена гипербола, и тем более сжата сама гипербола; чем больше величина , тем круче располагаются ветви гиперболы.
Но, так же как и для эллипса, в качестве характеристики формы гиперболы в аналитической геометрии пользуются не величиной отношения , а величиной 
, называемой эксцентриситетом гиперболы и обозначают той же буквой , как и для эллипса:
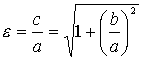(3.25).
Так как у гиперболы 
, то эксцентриситет гиперболы 
.
Из прямоугольного треугольника 
, в котором острый угол наклона асимптоты к вещественной оси обозначен через 
, находим:
и, следовательно:
(3.26),
т. е. эксцентриситет гиперболы равен секансу угла наклона асимптоты к вещественной оси.
Важным частным случаем гиперболы является равносторонняя (равноосная) гипербола – такая гипербола, у которой равны длины вещественной и мнимой полуосей: .
Уравнение этой гиперболы имеет вид:
(3.27).
У равносторонней гиперболы, как нетрудно показать, угол между асимптотами прямой, 
и 
.
Для гиперболы, у которых оси совпадают и равны, но вещественная ось одной служит мнимой осью другой и наоборот, называются сопряженными; асимптоты таких гипербол также совпадают (поскольку совпадают их осевые прямоугольники), но гиперболы располагаются в смежных углах между асимптотами.
Нетрудно видеть, что если уравнением одной из сопряженных гипербол является уравнение (3.21):
,
то уравнение второй будет иметь вид:
,
или 
(3.28),
поскольку меняются ролями оси Ox и Oy и полуоси гипербол а и b.
Отметим, что расстояние с от центра до фокусов у обеих сопряженных гипербол одно и то же, определяемое формулой (3.24), но эксцентриситеты различные: 
, 
;
(если только обе гиперболы не являются равносторонними).
4.4. Парабола
Параболой называется геометрическое место точек плоскости, расстояния которых от заданных на той же плоскости точки (фокуса параболы) и прямой (директрисы параболы) равны между собой.
Пусть точка F – фокус; прямая KL – директриса параболы; М – произвольная точка параболы.
По определению параболы:
(3.29),
где В – основание перпендикуляра, опущенного из точки М на директрису KL.
Введем обозначение 
, где 
– основание перпендикуляра, опущенного из фокуса на директрису; величину 
, расстояние от фокуса до директрисы, называют параметром параболы.
Для вывода простейшего уравнения параболы оси координат расположим следующим образом: начало координат поместим в точку О – середину отрезка 
; за ось 
примем прямую, которой принадлежит отрезок , причем за положительное ее направление примем направление от точки О к фокусу F; ось 
направим перпендикулярно оси , т. е. параллельно директрисе.
При таком выборе осей координаты фокуса 
будут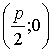 
, а уравнение директрисы 
.
Для точки 
, лежащей на параболе, имеем:
, 
;
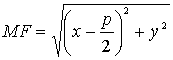подставляя эти значения в равенство (3.29), получаем:
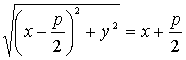(3.30).
Возведем обе части уравнения (3.30) в квадрат, одновременно раскрывая скобки:
.
Приводя подобные члены, получим простейшее (каноническое) уравнение параболы:
(3.31).
Построим параболу по этому уравнению.
Прежде всего отметим, что вся парабола расположена справа от оси ; в самом деле, в уравнении (3.31) левая часть неотрицательна (
), в правой части 
; следовательно, и второй множитель правой части неотрицателен: 
.
Поскольку в уравнение (3.31) текущая координата 
входит только во второй степени, заключаем, что ось является осью симметрии параболы. При 
и 
: парабола проходит через начало координат; эту точку называют вершиной параболы.
При возрастании 
одновременно возрастает и абсолютная величина 
, ибо 
.
При построении параболы полезно помнить, что ордината точки 
параболы, лежащей над ее фокусом, равна параметру параболы 
; в самом деле, при 
из уравнения параболы (3.31) находим:
, откуда
.
Таким образом, длина хорды 
параболы, проходящей через ее фокус перпендикулярно оси параболы, равна 
.
Если повернуть параболу относительно осей координат на угол 
против часовой стрелки, то в уравнении (3.31) координаты 
и 
поменяются местами и уравнение такой параболы запишется так:
(3.32)
Вершиной этой параболы по-прежнему является начало координат, но осью симметрии будет служить ось ; парабола лежит над осью 
.
Фокусом этой параболы будет точка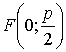 
; директрисой – прямая 
(рис. 3.8).
Нетрудно далее убедиться в том, что уравнения:
(3.33)
и
(3.34)
(в обоих случаях 
) также определяют параболы, которые от парабол, определяемых уравнениями (3.31) и (3.32), отличаются только тем, что они направлены в сторону, противоположную направлению соответствующих координатных осей: первая – вдоль отрицательной оси , вторая – вдоль отрицательной оси .
Рекомендуем читателю самому найти координаты фокусов этих парабол и уравнения их директрис.
Уравнения парабол (3.31) и (3.33) можно записать в виде единого уравнения:
(3.31`),
а уравнения парабол (3.32) и (3.34) – в виде уравнения:
(3.32`),
если в уравнениях (3.31') и (3.32') рассматривать 
как коэффициент, принимающий и положительные, и отрицательные значения (параметр параболы будет равен 
).
При 
парабола будет направлена в положительном направлении соответствующей оси координат, а при 
– в отрицательном.