На практике все сигналы, которые предназначены для передачи информации, носят случайный характер. Именно в случайности изменения сигналов заложена информация, которую необходимо передать получателю. Помимо этого, при передаче сигналов действуют помехи, которые также носят случайный характер.
В отличие от детерминированных сигналов значения случайного сигнала в некоторый момент времени невозможно предсказать точно. Вместе с тем, описание таких сигналов возможно в вероятностном смысле через усредненные (статистические) характеристики. Поэтому, прежде чем перейти к изучению случайных сигналов целесообразно рассмотреть основные положения теории вероятностей.
Подобно тому, как в алгебре основным понятием является число, а в геометрии – точка, линия, плоскость, в теории вероятностей основным понятием является случайное событие, которое при проведении эксперимента может произойти, а может и не произойти. Если, например, проводится эксперимент, включающий серию из n испытаний радиотехнического устройства, то результатом каждого испытания может быть либо рабочее состояние устройства, либо его отказ, которые представляют собой события. Но при каждом конкретном испытании отказ может произойти, а может и не произойти. В этом смысле отказ является случайным событием. Обозначим случайное событие буквой ![]() .
.
Центральным в теории вероятностей является определение частости (или частоты) наступления события ![]()
![]() , (5.1)
, (5.1)
где ![]() – число испытаний, соответствующих наступлению со бытия
– число испытаний, соответствующих наступлению со бытия ![]() ,
,
![]() – общее число все проведенных испытаний.
– общее число все проведенных испытаний.
При достаточно большом числе всех проведенных испытаний (теоретически при ![]() ) частость наступления события
) частость наступления события ![]() отождествляется с вероятностью
отождествляется с вероятностью
![]() . (5.2)
. (5.2)
Из данного определения следует, что
![]() , (5.3)
, (5.3)
т.е. вероятность является неотрицательной величиной, принимающей значение в диапазоне чисел от 0 до 1.
Событие ![]() , для которого
, для которого ![]() , называется невозможным, а событие для которого
, называется невозможным, а событие для которого ![]() – достоверным.
– достоверным.
Понятие вероятности можно распространить на совокупность событий. Если ![]() – множество всех случайных событий, то
– множество всех случайных событий, то ![]() – вероятность наступления события
– вероятность наступления события ![]() . В рассмотренном примере
. В рассмотренном примере ![]() , где
, где ![]() – отказ устройства,
– отказ устройства, ![]() – рабочее состояние.
– рабочее состояние.
Множество ![]() событий образуют полную группу, если в результате испытания одно из событий множества наступит обязательно. События рассмотренного выше примера образуют полную группу. Очевидно, для полной группы событий справедливо равенство
событий образуют полную группу, если в результате испытания одно из событий множества наступит обязательно. События рассмотренного выше примера образуют полную группу. Очевидно, для полной группы событий справедливо равенство
![]() .
.
События ![]() и
и ![]() называются несовместными, если появление одного из них исключает появление другого. События
называются несовместными, если появление одного из них исключает появление другого. События ![]() и
и ![]() рассмотренного примера являются несовместными. Вероятность наступления одного из них, т.е. события
рассмотренного примера являются несовместными. Вероятность наступления одного из них, т.е. события ![]() или события
или события ![]() , или …, события
, или …, события ![]() , …, или события
, …, или события ![]() равна сумме вероятностей этих событий
равна сумме вероятностей этих событий
![]() . (5.5)
. (5.5)
Если в результате эксперимента возможно одновременное наступление событий, например, при включении радиоприемника он является исправным (событие ![]() ) и настроен на произвольную частоту (событие
) и настроен на произвольную частоту (событие ![]() ), то такие события называются совместными. В этом случае говорят, что событие
), то такие события называются совместными. В этом случае говорят, что событие ![]() влечет за собой событие
влечет за собой событие ![]() и такая ситуация обозначается
и такая ситуация обозначается ![]() . Вероятность наступления события
. Вероятность наступления события ![]() , если произошло событие
, если произошло событие ![]() называется условной вероятностью
называется условной вероятностью 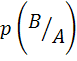 . Очевидно, вероятность одновременного наступления совместных событий
. Очевидно, вероятность одновременного наступления совместных событий ![]() и
и ![]() определяется соотношением
определяется соотношением
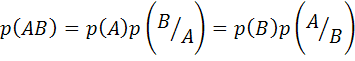 . (5.6)
. (5.6)
События ![]() и
и ![]() называются независимыми, если наступление одного из них не связано с наступлением другого. Вероятность наступления двух независимых совместных событий равна
называются независимыми, если наступление одного из них не связано с наступлением другого. Вероятность наступления двух независимых совместных событий равна
![]() . (5.7)
. (5.7)
Отсюда следует, что для независимых совместных событий условная вероятность 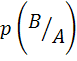 равна безусловной вероятности
равна безусловной вероятности ![]() .
.
Вероятность события ![]() , которое может наступить с одним из событий
, которое может наступить с одним из событий ![]() , образующих полную группу несовместных событий, называемых гипотезами, определяется формулой полной вероятности
, образующих полную группу несовместных событий, называемых гипотезами, определяется формулой полной вероятности
![]() . (5.8)
. (5.8)
Вероятность наступления гипотезы ![]() , после того как наступило событие
, после того как наступило событие ![]() , определяется формулой Байеса
, определяется формулой Байеса
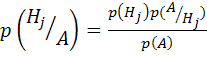 , (5.9)
, (5.9)
где ![]() вычисляется в соответствии с (5.8).
вычисляется в соответствии с (5.8).
Случайные события характеризуют эксперимент с качественной стороны. На практике пользуются количественной оценкой результата. Если в результате эксперимента наступает или не наступает событие ![]() (в рассмотренном примере отказ радиотехнического устройства), этому случайному событию можно поставить в соответствие величину, принимающую только два значения: 1 или 0 в зависимости от того, произошло событие или нет. Так как событие
(в рассмотренном примере отказ радиотехнического устройства), этому случайному событию можно поставить в соответствие величину, принимающую только два значения: 1 или 0 в зависимости от того, произошло событие или нет. Так как событие ![]() случайно, случайной будет и величина (СВ), оценивающая результат эксперимента. Очевидно, вероятность наступления события
случайно, случайной будет и величина (СВ), оценивающая результат эксперимента. Очевидно, вероятность наступления события ![]() в рассматриваемом примере совпадает с вероятностью того, что случайная величина принимает значение, равное 1.
в рассматриваемом примере совпадает с вероятностью того, что случайная величина принимает значение, равное 1.
Обозначим случайную величину через ![]() , а значения, которые она может принимать,− через
, а значения, которые она может принимать,− через ![]() . Если случайная величина
. Если случайная величина ![]() принимает значения из множества
принимает значения из множества ![]() , элементы которого можно перенумеровать, то такая случайная величина называется дискретной СВ. Если же множество
, элементы которого можно перенумеровать, то такая случайная величина называется дискретной СВ. Если же множество ![]() значений непрерывно, т.е. перенумеровать значения невозможно, то такая величина называется непрерывной СВ.
значений непрерывно, т.е. перенумеровать значения невозможно, то такая величина называется непрерывной СВ.
Как дискретная, так и непрерывная СВ полностью характеризуются законами распределения. Функцией распределения (интегральным законом) дискретной СВ называется зависимость
![]() , (5.10)
, (5.10)
т.е. зависимость вероятности того, что случайная величина ![]() не превосходит значения
не превосходит значения ![]() , где
, где ![]() принимает значения от
принимает значения от ![]() до
до ![]() .
.
Рядом распределения дискретной СВ называется совокупность всех возможных значений ![]() и соответствующих им вероятностей
и соответствующих им вероятностей
![]() . (5.11)
. (5.11)
Ряд распределения задается либо выражением (5.11), либо в виде таблицы. Очевидно
![]() . (5.12)
. (5.12)
Функция распределения непрерывной СВ представляет собой зависимость
![]() , (5.13)
, (5.13)
и является интегральным законом распределения непрерывной СВ.
Плотностью распределения непрерывной СВ называется зависимость
![]() , (5.14)
, (5.14)
где ![]() , и представляет собой отношение вероятности
, и представляет собой отношение вероятности ![]() того, что непрерывная СВ будет находиться в пределах элементарного интервала
того, что непрерывная СВ будет находиться в пределах элементарного интервала ![]() к величине этого интервала. Если функция
к величине этого интервала. Если функция ![]() непрерывна и интервал значений СВ составляет (
непрерывна и интервал значений СВ составляет ( ![]() ), то функция распределения и плотность распределения связаны между собой соотношениями
), то функция распределения и плотность распределения связаны между собой соотношениями
![]() , (5.15)
, (5.15)
![]() . (5.16)
. (5.16)
Из (5.16) следует, что плотность распределения представляет собой дифференциальный закон распределения вероятностей.
На рис. 5.1 изображены графики функции распределения и ряда распределения дискретной СВ (рис. 5.1а,б) и функции распределения и плотности распределения (рис. 5.1в,г) непрерывной СВ.
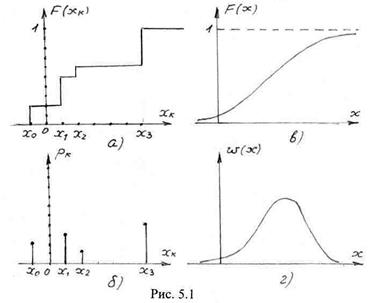 Основные свойства функции распределения:
Основные свойства функции распределения:
− функция распределения (для дискретной СВ – ступенчатая, для непрерывной СВ – непрерывная) является монотонно-возрастающей неотрицательной функцией;
− при ![]() для дискретной СВ и
для дискретной СВ и ![]() для непрерывной СВ функция распределения равна нулю;
для непрерывной СВ функция распределения равна нулю;
− при ![]() для дискретной СВ и
для дискретной СВ и ![]() для непрерывной СВ функция распределения
для непрерывной СВ функция распределения ![]() ;
;
− вероятность попадания СВ в интервал (a,b) равна
![]() . (5.16)
. (5.16)
Основные свойства плотности распределения вероятностей непрерывной СВ:
− плотность вероятности величина неотрицательная, т.е.
![]() , при
, при ![]() ;
;
− вероятность попадания непрерывной СВ в интервал (a,b) равна
![]() . (5.17)
. (5.17)
Отсюда следует, что вероятность попадания СВ в интервал ( ![]() )
)
![]() . (5.18)
. (5.18)
Выражение (5.18) представляет собой условие нормировки. Это означает, что площадь под кривой ![]() равна единице.
равна единице.
Хотя законы распределения в полной мере характеризуют случайную величину, на практике более широко используются числовые характеристики, получаемые усреднением значений самой СВ. числовые характеристики СВ называют моментами. Различают начальные и центральные моменты СВ.
Начальным моментом n-го порядка являются величины:
− для дискретной СВ
![]() , (5.19)
, (5.19)
− для непрерывной СВ
![]() . (5.20)
. (5.20)
Начальный момент первого порядка (n=1) называется математическим ожиданием:
− для дискретной СВ
![]() , (5.21)
, (5.21)
− для непрерывной СВ
![]() . (5.22)
. (5.22)
Математическое ожидание является средним значением СВ.
Центральным моментом n-го порядка является:
− для дискретной СВ
![]() , (5.23)
, (5.23)
− для непрерывной СВ
![]() . (5.24)
. (5.24)
Центральный момент второго порядка называется дисперсией СВ.
Дисперсия:
− для дискретной СВ
![]() , (5.25)
, (5.25)
− для непрерывной СВ
![]() . (5.26)
. (5.26)
Если случайная величина ![]() физически является электрической величиной, то начальный момент второго порядка представляет собой среднюю мощность СВ, а дисперсия – отклонение мощности от ее среднего значения. Величина
физически является электрической величиной, то начальный момент второго порядка представляет собой среднюю мощность СВ, а дисперсия – отклонение мощности от ее среднего значения. Величина ![]() называется среднеквадратичным отклонением (СКО).
называется среднеквадратичным отклонением (СКО).
В практической радиотехнике наиболее широко используются следующие законы распределения, которые обычно описываются рядом распределения для дискретных СВ и плотностью вероятности – для непрерывных СВ.
Для дискретных СВ
− равномерный закон:
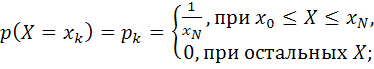 (5.27)
(5.27)
− биномиальный закон определяет вероятность числа k появления случайного события при n независимых испытаниях (например, вероятность появления k единиц в кодовой комбинации из n разрядов):
![]() , (5.28)
, (5.28)
Где ![]() − число сочетаний из n по k,
− число сочетаний из n по k,
p – вероятность появления события (вероятность появления единицы в кодовой комбинации).
Для непрерывных СВ
− равномерный закон
![]() , (5.29)
, (5.29)
где (a,b) – область определения случайной величины;
− нормальный закон
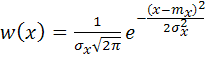 , (5.30)
, (5.30)
где ![]() – математическое ожидание,
– математическое ожидание,
![]() – дисперсия случайной величины.
– дисперсия случайной величины.
Для практических расчетов при решении задач радиотехники используют закон нормально распределенной СВ с нулевым математическим ожиданием ![]() и единичной дисперсией
и единичной дисперсией ![]() . Тогда плотность вероятности
. Тогда плотность вероятности
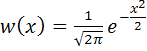 ,
,
а функция распределения
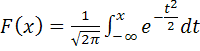 . (5.31)
. (5.31)
Выражение (5.31) называется интегралом вероятности. Его значения рассчитаны и сведены в таблицу, которую можно найти в литературе;
− закон Рэлея определяет распределения модуля вектора на плоскости, составляющие которого по обеим осям независимы и распределены нормально с нулевым математическим ожиданием и дисперсией ![]()
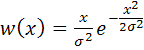 . (5.32)
. (5.32)
Понятия законов распределения можно распространить и на совокупность случайных величин. Так для двух случайных величин ![]() и
и ![]() функцией распределения называется вероятность того, что случайная величина
функцией распределения называется вероятность того, что случайная величина ![]() не превзойдет значения
не превзойдет значения ![]()
![]() . (5.33)
. (5.33)
Очевидно, функция (5.33) является двумерной.
Двумерная плотность распределения двух СВ
![]() . (5.34)
. (5.34)
На рис. 5.2 изображена двумерная плотность ![]() . Так же, как одномерная
. Так же, как одномерная ![]() двумерная плотность неотрицательна
двумерная плотность неотрицательна
![]() .
.
Условие нормировки
![]() . (5.35)
. (5.35)
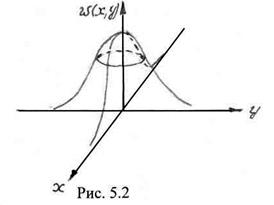 Очевидно, из (5.35) вытекает, что объем под поверхностью
Очевидно, из (5.35) вытекает, что объем под поверхностью ![]() равен единице.
равен единице.
По заданной двумерной плотности можно найти одномерные плотности ![]() и
и ![]() . Так
. Так
![]() . (5.36)
. (5.36)
Если случайные величины ![]() и
и ![]() независимы, то
независимы, то
![]() . (5.37)
. (5.37)
При наличии зависимости случайных величин
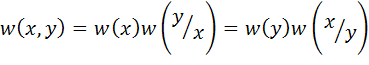 . (5.38)
. (5.38)
Для зависимых случайных величин имеет место коэффициент корреляции
![]() , (5.39)
, (5.39)
характеризующий степень зависимости этих величин.

